A block moving horizontally on a smooth surface with a speed of 40 m/s splits into two parts with messes in the ratio of 1:2 If the smaller part moves at 60 m/s in the same direction , then fractional change in kinetic energy is :
23
18
12
14
To solve the problem, we will go through the following steps:
Step 1: Understand the problem and define variables
We have a block moving horizontally with a speed of v=40m/s that splits into two parts with masses in the ratio of 1:2. Let's denote the total mass of the block as M. Therefore, we can define:
- Mass of the smaller part, m1=M3
- Mass of the larger part, m2=2M3
Step 2: Use conservation of momentum
Since no external forces are acting on the system, we can use the conservation of momentum. The initial momentum of the block is:
Pinitial=M⋅v=M⋅40
After the split, the smaller part moves with a velocity of v1=60m/s, and we need to find the velocity of the larger part, v2. The momentum after the split is:
Pfinal=m1⋅v1+m2⋅v2
Substituting the values:
M⋅40=M3⋅60+2M3⋅v2
Dividing through by M (assuming M≠0):
40=603+23v2
This simplifies to:
40=20+23v2
Subtracting 20 from both sides gives:
20=23v2
Multiplying both sides by 32:
v2=30m/s
Step 3: Calculate initial and final kinetic energy
The initial kinetic energy KEinitial of the block is given by:
KEinitial=12Mv2=12M(40)2=800MJ
The final kinetic energy KEfinal after the split is the sum of the kinetic energies of both parts:
KEfinal=12m1v21+12m2v22
Substituting the values:
KEfinal=12(M3)(60)2+12(2M3)(30)2
Calculating each term:
=16M(3600)+13M(900)=600M+300M=900MJ
Step 4: Calculate the fractional change in kinetic energy
The change in kinetic energy is:
ΔKE=KEfinal−KEinitial=900M−800M=100M
The fractional change in kinetic energy is:
Fractional Change=ΔKEKEinitial=100M800M=18
Final Answer
The fractional change in kinetic energy is 18.
---
We have a block moving horizontally with a speed of v=40m/s that splits into two parts with masses in the ratio of 1:2. Let's denote the total mass of the block as M. Therefore, we can define:
- Mass of the smaller part, m1=M3
- Mass of the larger part, m2=2M3
Since no external forces are acting on the system, we can use the conservation of momentum. The initial momentum of the block is:
Pinitial=M⋅v=M⋅40
After the split, the smaller part moves with a velocity of v1=60m/s, and we need to find the velocity of the larger part, v2. The momentum after the split is:
Pfinal=m1⋅v1+m2⋅v2
Substituting the values:
M⋅40=M3⋅60+2M3⋅v2
Dividing through by M (assuming M≠0):
40=603+23v2
This simplifies to:
40=20+23v2
Subtracting 20 from both sides gives:
20=23v2
Multiplying both sides by 32:
v2=30m/s
The initial kinetic energy KEinitial of the block is given by:
KEinitial=12Mv2=12M(40)2=800MJ
KEfinal=12m1v21+12m2v22
Substituting the values:
KEfinal=12(M3)(60)2+12(2M3)(30)2
Calculating each term:
=16M(3600)+13M(900)=600M+300M=900MJ
The change in kinetic energy is:
ΔKE=KEfinal−KEinitial=900M−800M=100M
The fractional change in kinetic energy is:
Fractional Change=ΔKEKEinitial=100M800M=18
The fractional change in kinetic energy is 18.
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section A )
20 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics Section B
20 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
A block moving horizontally on a smooth surface with a speed of 40 ms−1 splits into two equal parts. If one of the parts moves at 60 ms1 in the same direction, then the fractional change in the kinetic energy will be x : 4 where x =__________
View SolutionA block movig horizontally ona smooth surace with a speed of 20 m/s bursts into thwo equal parts cobtinuing in the same direction. If one of the parts moves at 30 m/s, with whast speed does the second part move and what is tehfractional change in the kinetic energy?
View Solution
Knowledge Check
A light particle moving horizontally with a speed of 12 m/s strikes a very heavy block moving in the same direction at 10 m/s. The collision is one dimensional and elastic. After the collision, the particle will be
 Amove at 2 m/s in its original directionBmove at 8 m/s in its original directionCmove at 8 m/s opposite to its original directionDmove at 12 m/s opposite to its original direction
Amove at 2 m/s in its original directionBmove at 8 m/s in its original directionCmove at 8 m/s opposite to its original directionDmove at 12 m/s opposite to its original directionA 15kg block is initially moving along a smooth horizontal surface with a speed of v=4m/s to the left. It is acted by a force F , which varies in the manner shown. Determine the velocity of the block at t=15 seconds.
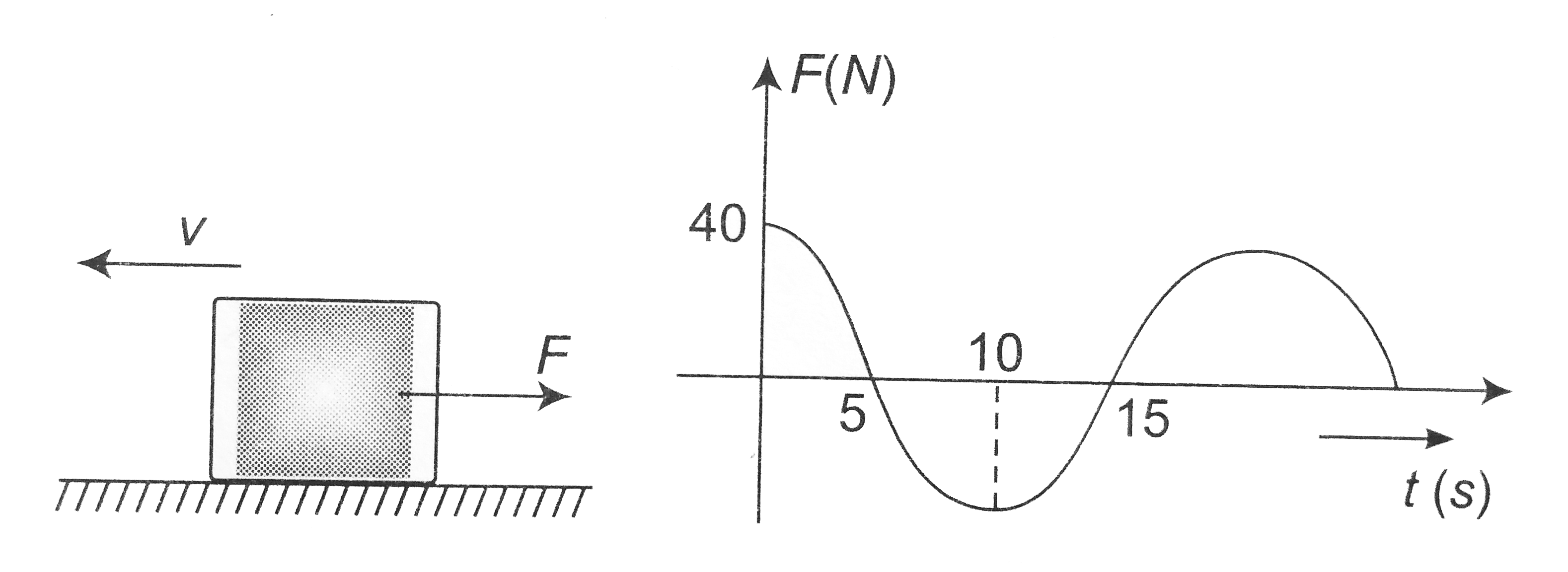 A12.5m/sB8.5m/sC20m/sD9.5m/s
A12.5m/sB8.5m/sC20m/sD9.5m/sA bomb of 12 kg divides in two parts whose ratio of masses is 1 : 3. If kinetic energy of smaller part is 216 J , then momentum of bigger part in kg m / sec will be
A36B72C108DData is incomplete
A particle is moving along x-axis with velocity 40 m/s. It breaks into two parts in mass ratio 1:2. If speed of smaller part is 60 m/s along x-axis then find fractional changes in kinetic energy of system.
View SolutionRelative speed of two persons moving with u m/s and v m/s in same direction where u>v
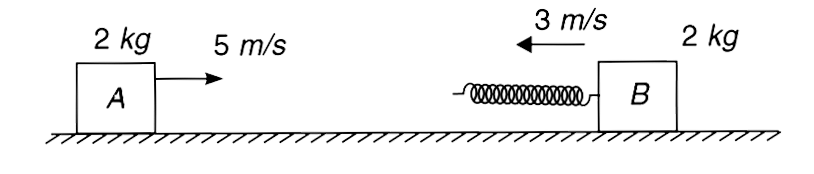
View SolutionA block A of mass 2kg is moving to right with a speed of 5 m/s on a horizontal smooth surface. Another block B of mass 2 kg, with a mass less spring of force constant K=200 N/m attached to it, is moving to left on the same surface with a speed of 3 m/s. Block A collides with the spring attached to B. Calculate
(a) the final velocity of the block A.
(b) the minimum kinetic energy of the system of two blocks during subsequent motion.
(c) Repeat part (b) if there is no spring and the two blocks collide head on. Assume that the blocks are made of perfectly elastic material
View SolutionA block of 10kg mass is thrown on a rough surface having friction coefficient 0.3 with an initial speed of 5 m/s. Find the amount by which the internal energy of the blocked and the surface will increase. If this block is seen from a frame moving at a speed of 5 m/s in the direction of its velocity it is observed that the block is gently put on the rough surface moving in opposite direction at speed 5 m/s. Find the gain kinetic energy of the block as seen from this frame.
View SolutionTwo objects having equal masses are moving with uniform velocities of 2 m/s and 6 m/s respectively. Calculate the ratio of their kinetic energies.
View Solution