Statement 1: Three force →f1, →f2 and →f3 are acted at vertices of a triangular body such that →f1+→f2=−→f3 and these force are concurrent forces,
Statement 2: It explain translations equilibrium
Both Statements correct
Statement 1 incorrect and Statement 2 correct
Statement 2 incorrect and Statement 1 correct
Both Statements incorrect
To solve the problem, we need to analyze the statements given regarding the forces acting on a triangular body.
1. Understanding Concurrent Forces:
- Concurrent forces are defined as forces whose lines of action intersect at a common point. In this case, we have three forces, →f1, →f2, and →f3, acting at the vertices of a triangular body.
Hint: Recall the definition of concurrent forces and visualize how they act on a triangular body.
2. Analyzing Statement 1:
- The statement says →f1+→f2=−→f3. This can be rearranged to →f1+→f2+→f3=0. This equation indicates that the vector sum of the forces is zero, which is a condition for translational equilibrium.
Hint: Remember that for a body to be in equilibrium, the vector sum of all forces acting on it must be zero.
3. Understanding Translational Equilibrium:
- Translational equilibrium occurs when the net force acting on a body is zero. Since we derived that →f1+→f2+→f3=0, it implies that the body is in translational equilibrium.
Hint: Consider the implications of net force being zero on the motion of the body.
4. Analyzing Statement 2:
- Statement 2 claims that the situation explains translational equilibrium. Since we have established that the sum of the forces equals zero, this statement is also correct.
Hint: Think about how the conditions for equilibrium relate to the forces acting on the body.
5. Conclusion:
- Both statements are correct. Statement 1 correctly describes the relationship between the forces, and Statement 2 correctly identifies that this relationship leads to translational equilibrium.
Final Answer: Both statements are correct.
- Concurrent forces are defined as forces whose lines of action intersect at a common point. In this case, we have three forces, →f1, →f2, and →f3, acting at the vertices of a triangular body.
- The statement says →f1+→f2=−→f3. This can be rearranged to →f1+→f2+→f3=0. This equation indicates that the vector sum of the forces is zero, which is a condition for translational equilibrium.
- Translational equilibrium occurs when the net force acting on a body is zero. Since we derived that →f1+→f2+→f3=0, it implies that the body is in translational equilibrium.
- Statement 2 claims that the situation explains translational equilibrium. Since we have established that the sum of the forces equals zero, this statement is also correct.
- Both statements are correct. Statement 1 correctly describes the relationship between the forces, and Statement 2 correctly identifies that this relationship leads to translational equilibrium.
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A80videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B40videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions473videos
JEE MAIN
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question492videos
JEE MAIN 2022
Similar Questions
If three forces −→F1,+−→F2and−→F3 are represented by three sides of a triangle and −→F1+−→F2=−−→F3 , then these three forces are concurrent forces and satisfy the condition for equilibrium .
Statement II : A triangle made up of three forces →F1,→F2and→F3 as sides taken in the same order ,satisfy the condition for translatory equilibrium . In the light of the above statements ,choose the most appropriate answer from the options given below :View SolutionThree forces (→F1,→F2,→F3) are acting an a particle moving vertically up with constant speed. Two force →F1=−10ˆjN, and →F1=−6ˆi=8ˆj , N are acting an particle on acting on particle respectively find →F3.
View Solution
Knowledge Check
- Question 1 - Select One
Two forces −→F1and−→F2 are acting at right angles to each other , find their resultant ?
A√F21−F22B√F21+F22C√(F1+F2)DF1+F2 - Question 2 - Select One
Three forces →F1,→F2 and →F3 are represented as shown. Each of them is equal magnitude.
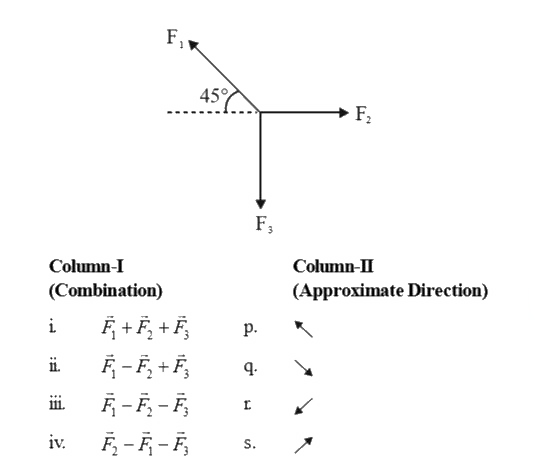
Now match the given columns and select the correct option from the codes given below.Ai-p,ii-q,iii-r,iv-sBi-s,ii-r,iii-q,iv-pCi-q,ii-r,iii-p,iv-sDi-r,ii-s,iii-p,iv-q - Question 3 - Select One
When force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
A→F1/mB→F1/mC→F2−→F3/mD→F2/m
If a force →F=(→i+2→j+→k)N acts on a body produces a displacement of →S=(4→i+→j+7→k)m, then the work done is
View SolutionIf →F is the force acting in a particle having position vector →r and →τ be the torque of this force about the origin, then
View SolutionTwo forces →F1=500N due east and →F2=250N due north have their common initial point. →F2−→F1 is
View SolutionWhen force −→F1,−→F2,−→F3…...−→Fn act on a particle , the particle remains in equilibrium . If −→F1 is now removed then acceleration of the particle is
View SolutionA body placed in free space, is simultaneously acted upon by three forces −→F1,−→F2 and −→F3. The body is in equilibrium and the forces −→F1 and −→F2 are known ot be 36 N due north and 27 N due east respectively. Which of the following best describes the force −→F3?
View Solution

