A varying magnetic field exist in space as follows B=B0(ˆi+ˆj√2[cos(kz−wt)] two charge particles q1=4π C and q2=2π C placed at (0,0,πk) and (0,0,3πk) and moving with equal velocities of 0.5cˆi then find ratio of force on two charge at t= 0s is
2
4
6
8
To solve the problem, we need to find the ratio of the forces acting on two charged particles q1 and q2 due to a varying magnetic field at t=0 seconds.
1. Identify the Magnetic Field:
The magnetic field is given by:
B=B0(^i+^j)√2cos(kz−ωt)
At t=0:
B=B0(^i+^j)√2cos(kz)
2. Determine the Positions of the Charges:
- Charge q1=4πC is located at (0,0,πk).
- Charge q2=2πC is located at (0,0,3πk).
3. Calculate the Magnetic Field at the Positions of the Charges:
- For charge q1:
B1=B0(^i+^j)√2cos(k⋅πk)=B0(^i+^j)√2cos(π)=−B0(^i+^j)√2
- For charge q2:
B2=B0(^i+^j)√2cos(k⋅3πk)=B0(^i+^j)√2cos(3π)=−B0(^i+^j)√2
Thus, we have:
B1=B2=−B0(^i+^j)√2
4. Determine the Velocity of the Charges:
Both charges are moving with the same velocity:
v=0.5c^i
5. Calculate the Forces on the Charges:
The magnetic force on a charge in a magnetic field is given by:
F=qv×B
- For charge q1:
F1=q1v×B1=4π⋅(0.5c^i)×(−B0(^i+^j)√2)
Using the cross product:
^i×^i=0,^i×^j=^k⇒F1=4π⋅(0.5c)⋅(−B01√2)^k=−2πcB01√2^k
- For charge q2:
F2=q2v×B2=2π⋅(0.5c^i)×(−B0(^i+^j)√2)
Similarly, we find:
F2=2π⋅(0.5c)⋅(−B01√2)^k=−πcB01√2^k
6. Find the Ratio of the Forces:
The ratio of the forces is:
F1F2=−2πcB01√2−πcB01√2=2ππ=2
Final Answer:
The ratio of the forces on the two charges at t=0 seconds is:
F1F2=2
The magnetic field is given by:
B=B0(^i+^j)√2cos(kz−ωt)
At t=0:
B=B0(^i+^j)√2cos(kz)
- Charge q1=4πC is located at (0,0,πk).
- Charge q2=2πC is located at (0,0,3πk).
- For charge q1:
B1=B0(^i+^j)√2cos(k⋅πk)=B0(^i+^j)√2cos(π)=−B0(^i+^j)√2
- For charge q2:
B2=B0(^i+^j)√2cos(k⋅3πk)=B0(^i+^j)√2cos(3π)=−B0(^i+^j)√2
B1=B2=−B0(^i+^j)√2
Both charges are moving with the same velocity:
v=0.5c^i
The magnetic force on a charge in a magnetic field is given by:
F=qv×B
- For charge q1:
F1=q1v×B1=4π⋅(0.5c^i)×(−B0(^i+^j)√2)
Using the cross product:
^i×^i=0,^i×^j=^k⇒F1=4π⋅(0.5c)⋅(−B01√2)^k=−2πcB01√2^k
F2=q2v×B2=2π⋅(0.5c^i)×(−B0(^i+^j)√2)
Similarly, we find:
F2=2π⋅(0.5c)⋅(−B01√2)^k=−πcB01√2^k
The ratio of the forces is:
F1F2=−2πcB01√2−πcB01√2=2ππ=2
The ratio of the forces on the two charges at t=0 seconds is:
F1F2=2
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A80videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B40videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions473videos
JEE MAIN
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question492videos
JEE MAIN 2022
Similar Questions
The magnetic field vector of an electromagnetic wave is given by B=B0ˆi+ˆj√2cos(kz−ωt), where ˆi,ˆj represents unit vector along x and y - axis repectively .At t=0 s , two electric charges q1of 4π coulomb and q2 of 2π coulmb located at (0,0,πk)and(0,0,3πk), repectively ,have the same velocity of 0.5cˆi ,(where c is the velocity of light ).The ratio of the force actig on charge q1 to q2 is :
View SolutionElectric field and magnetic field in a region of space are given by(Ē= E_0 hat j). and (¯¯¯B=B0ˆj). A charge particle is released at origin with velocity (¯v=v0ˆk) then path of particle is
View Solution
Knowledge Check
- Question 1 - Select One
Electric field in space is given by −−→E(t)=E0i+j√2cos(ωt+Kz). A positively charged particle at (0,0,πK) is given velocity v0ˆk at t = 0. Direction of force acting on particle is
Af = 0Bantiparallel to ˆi+ˆj√2Cparallel to ˆi+ˆj√2Dˆk - Question 2 - Select One
If a unit vector is represented by 0.5ˆi+0.8ˆj+cˆk , then the value of c is
A1B√0.11C√0.01D√0.39 - Question 3 - Select One
In a certain region static electric and magentic fields exist. The magnetic field is given by →B=B0(ˆi+2ˆj−4ˆk). If a test charge moving with a velocity, →υ=υ0(3ˆi−ˆj+2ˆk) experience no force in that region, then the electric field in the region, in SI units, is-
A→E=−υ0B0(ˆi+ˆj+7ˆk)B→E=−υ0B0(3ˆi−2ˆj−4ˆk)C→E=υ0B0(14ˆj+7ˆk)D→E=−υ0B0(14ˆj+7ˆk)
A charge of -20 C is placed in an electric field given by →E=(5ˆi−3ˆj+4ˆk)N/C. Find the force on the charge.
View SolutionElectric and magnetic field are directed as E0ˆi and B0ˆk, a particle of mass m and charge + q is released from position (0,2,0) from rest. The velocity of that particle at (x,5,0) is (5ˆi+12ˆj) the value of x will be
View SolutionA magnetic field →B=B0ˆj exists in the region a<x<2a and →B=−B0ˆi in the region 2a<x<3a, where B0 is positive constant. A positive point charge moving with a velocity →v=v0ˆi where v0 is a positive constant, enters.
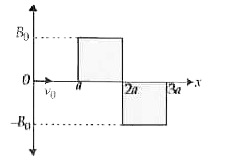
the magnetic field at x=a, The trajectory of the charge in this region can be like,View SolutionA magnetic field →B=B0ˆj , exists in the region a<x<2a , and vec(B) = -B_(0) hat(j),∈theregion2a lt xlt 3a,whereB_(0)isapositiveconstant.Apositivep∮char≥mov∈gwithavelocityvec(v) = v_(0) hat (i),wherev_(0) is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like
 View Solution
View SolutionIf a unit vector is represented by 0.5ˆi−0.8ˆj+cˆk, then the value of 'c' is :-
View Solution

