The magnetic field vector of an electromagnetic wave is given by $B = B_{0} \frac{ˆ i + ˆ j}{\sqrt{2}} cos (k z - ω t)$ , where $ˆ i, ˆ j$ represents unit vector along x and y - axis repectively .At t=0 s , two electric charges $q_{1}$ of $4 π$ coulomb and $q_{2}$ of $2 π$ coulmb located at $(0, 0, \frac{π}{k}) and (0, 0, \frac{3 π}{k})$ , repectively ,have the same velocity of $0.5 c ˆ i$ ,(where c is the velocity of light ).The ratio of the force actig on charge $q_{1}$ to $q_{2}$ is :

$2 : 1$

$2 \sqrt{2} : 1$

$1 : \sqrt{2}$

$\sqrt{2} : 1$

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to find the ratio of the forces acting on two charges $q_{1}$ and $q_{2}$ in a magnetic field generated by an electromagnetic wave. The magnetic field vector is given as:
$B = \frac{B_{0}}{\sqrt{2}} (^i +^j) cos (k z - ω t)$
Step 1: Evaluate the magnetic field at $t = 0$
At $t = 0$ , the magnetic field simplifies to:
$B = \frac{B_{0}}{\sqrt{2}} (^i +^j) cos (k z)$
Step 2: Calculate the magnetic field at the positions of the charges
For charge $q_{1}$ located at $(0, 0, \frac{π}{k})$ :
$B_{1} = \frac{B_{0}}{\sqrt{2}} (^i +^j) cos (k \cdot \frac{π}{k}) = \frac{B_{0}}{\sqrt{2}} (^i +^j) cos (π) = - \frac{B_{0}}{\sqrt{2}} (^i +^j)$
For charge $q_{2}$ located at $(0, 0, \frac{3 π}{k})$ :
$B_{2} = \frac{B_{0}}{\sqrt{2}} (^i +^j) cos (k \cdot \frac{3 π}{k}) = \frac{B_{0}}{\sqrt{2}} (^i +^j) cos (3 π) = - \frac{B_{0}}{\sqrt{2}} (^i +^j)$
Step 3: Calculate the forces on the charges
The force on a charge in a magnetic field is given by:
$F = q v \times B$
Both charges have the same velocity:
$v = 0.5 c^i$
For charge $q_{1} = 4 π$ :
$F_{1} = 4 π (0.5 c^i) \times (- \frac{B_{0}}{\sqrt{2}} (^i +^j))$
Calculating the cross product:
$F_{1} = 4 π (0.5 c) (- \frac{B_{0}}{\sqrt{2}}) (^i \times^i +^i \times^j) = 4 π (0.5 c) (- \frac{B_{0}}{\sqrt{2}}) (0 +^k) = - \frac{4 π B_{0} c}{2 \sqrt{2}}^k$
For charge $q_{2} = 2 π$ :
$F_{2} = 2 π (0.5 c^i) \times (- \frac{B_{0}}{\sqrt{2}} (^i +^j))$
Calculating the cross product:
$F_{2} = 2 π (0.5 c) (- \frac{B_{0}}{\sqrt{2}}) (^i \times^i +^i \times^j) = 2 π (0.5 c) (- \frac{B_{0}}{\sqrt{2}}) (0 +^k) = - \frac{2 π B_{0} c}{2 \sqrt{2}}^k$
Step 4: Find the ratio of the forces
Now, we can find the ratio of the magnitudes of the forces:
$\frac{| F_{1} |}{| F_{2} |} = \frac{\frac{4 π B_{0} c}{2 \sqrt{2}}}{\frac{2 π B_{0} c}{2 \sqrt{2}}} = \frac{4 π}{2 π} = 2$
Final Answer
The ratio of the force acting on charge $q_{1}$ to that on charge $q_{2}$ is:
$2$

Updated on:8/8/2024

The magnetic field of a plane electromagnetic wave is given by: $\to B = B_{0} ˆ i - [cos (k z - ω t)] + B_{1} ˆ j cos (k z + ω t)$ where $B_{0} = 3 \times 10^{- 5} T$ and $B_{1} = 2 \times 10^{- 6} T$ . The rms value of the force experienced by a stationary charge $Q = 10^{- 4} C$ at $z = 0$ is close to:
A0.1 N
B $3 \times 10^{- 2} N$
C0.6 N
D0.9 N
A charge particle $q_{1}$ , is at position (2, -1, 3). The electrostatic force on another charged particle $q_{2}$ at (0, 0, 0) is :
A $\frac{q_{1} q_{2}}{56 π \in_{0}} (2 ˆ i - ˆ j + 3 ˆ k)$
B $\frac{q_{1} q_{2}}{56 \sqrt{14} π \in_{0}} (2 ˆ i - ˆ j + 3 ˆ k)$
C $\frac{q_{1} q_{2}}{56 π \in_{0}} (ˆ j - 2 ˆ i - 3 ˆ k)$
D $\frac{q_{1} q_{2}}{56 \sqrt{14} π \in_{0}} (ˆ j - 2 ˆ i - 3 ˆ k)$
A system has two charges $q_{A} = + 2.5 \times 10^{- 7} C and q_{B} = + 2.5 \times 10^{- 7} C$ located at point A: (0,0,-15 cm)and B: (0,0,+15 cm), respectively. What are the total charge and eletric dipole moment of the system?

A $0$ , $0$
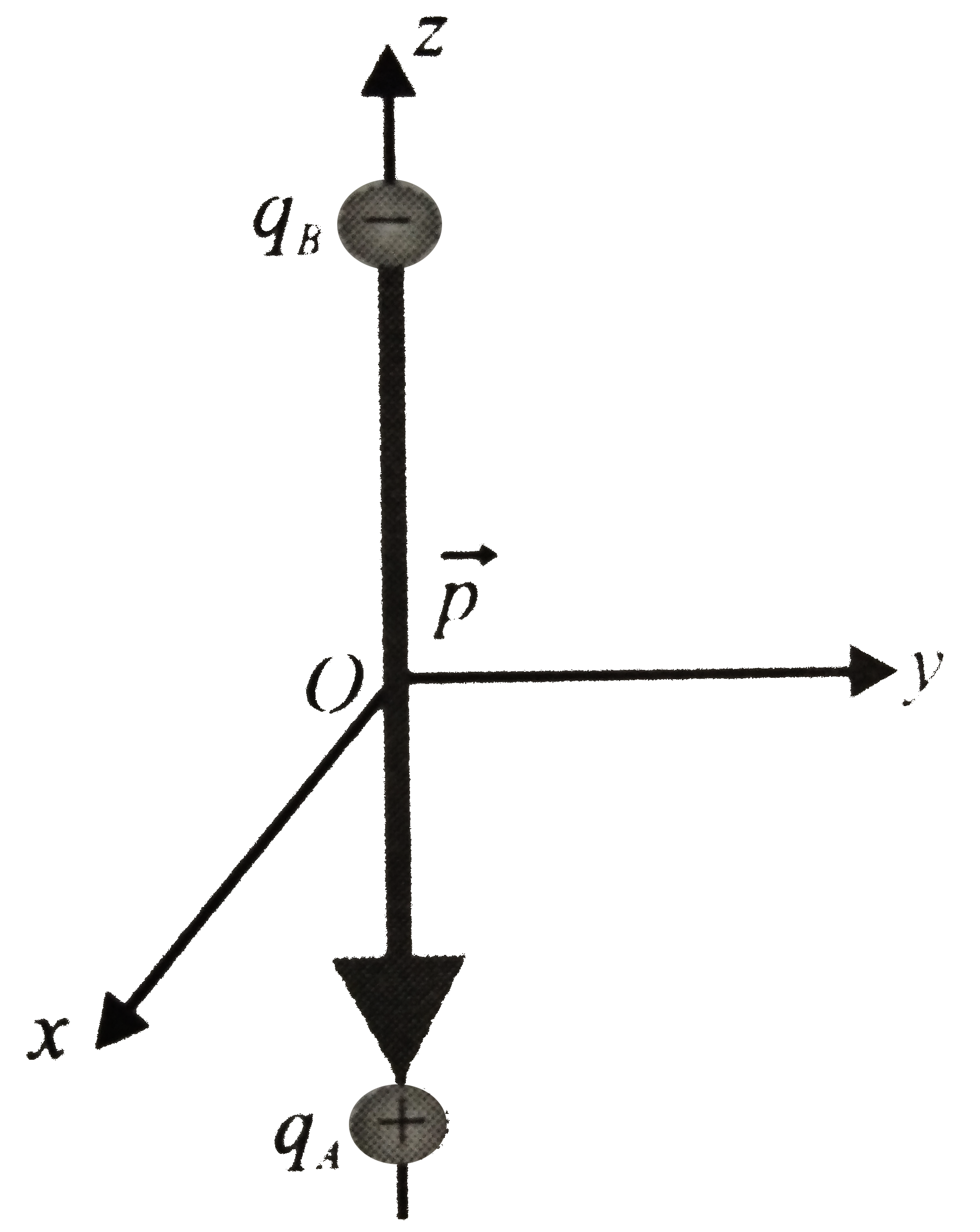B $7.5 \times 10^{- 8} C$ , $7.5 \times 10^{- 8} C m$
C $7.5 \times 10^{- 8} C$ , $0$
D $0$ , $7.5 \times 10^{- 8} C m$