Three Charges 2q, -q and -q lie at vertices of a triangle. The value of E and V at centroid of triangle will be-
E#0andV#0
E=0andV=0
E#0andV=0
E=0andV#0
To solve the problem of finding the electric field (E) and electric potential (V) at the centroid of a triangle formed by three charges (2q, -q, and -q), we will follow these steps:
Step 1: Understanding the Configuration
We have three charges placed at the vertices of a triangle:
- Charge 1: 2q at vertex A
- Charge 2: −q at vertex B
- Charge 3: −q at vertex C
The centroid of the triangle is the point where the medians intersect, and it is equidistant from all three vertices.
Step 2: Calculate the Electric Potential (V)
The electric potential V at a point due to a point charge is given by the formula:
V=kQr
where k=14πϵ0, Q is the charge, and r is the distance from the charge to the point of interest.
At the centroid, the distances from each charge to the centroid are equal. Let this distance be r.
The total electric potential V at the centroid due to the three charges is:
V=V2q+V−q+V−q
Substituting the values:
V=k2qr+k−qr+k−qr
V=k(2qr−qr−qr)
V=k(2q−q−qr)=k(0r)=0
Step 3: Calculate the Electric Field (E)
The electric field E due to a point charge is a vector quantity given by:
E=kQr2
We need to consider the direction of the electric fields due to each charge at the centroid.
1. Electric Field due to 2q: This field points away from the charge 2q towards the centroid.
2. Electric Field due to −q: This field points towards the charge −q at both vertices B and C.
Since the electric field is a vector, we need to consider the components of these fields. The symmetry of the triangle will lead to some cancellation of the components of the electric fields due to the two −q charges.
However, the net electric field will not be zero because the positive charge 2q will contribute a net electric field that does not have an equal opposing field from the two negative charges.
Conclusion
Thus, at the centroid of the triangle:
- The electric potential V=0
- The electric field E≠0 (it will have a specific non-zero value depending on the configuration, but we can conclude that it cannot be zero).
Final Answer
- Electric Potential V=0
- Electric Field E≠0
We have three charges placed at the vertices of a triangle:
- Charge 1: 2q at vertex A
- Charge 2: −q at vertex B
- Charge 3: −q at vertex C
The electric potential V at a point due to a point charge is given by the formula:
V=kQr
where k=14πϵ0, Q is the charge, and r is the distance from the charge to the point of interest.
V=V2q+V−q+V−q
Substituting the values:
V=k2qr+k−qr+k−qr
V=k(2qr−qr−qr)
V=k(2q−q−qr)=k(0r)=0
The electric field E due to a point charge is a vector quantity given by:
E=kQr2
We need to consider the direction of the electric fields due to each charge at the centroid.
2. Electric Field due to −q: This field points towards the charge −q at both vertices B and C.
Thus, at the centroid of the triangle:
- The electric potential V=0
- The electric field E≠0 (it will have a specific non-zero value depending on the configuration, but we can conclude that it cannot be zero).
- Electric Potential V=0
- Electric Field E≠0
Topper's Solved these Questions
- SAMPLE PAPER 2022BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - SECTION C
6 Videos
- SAMPLE PAPER 2022BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - SECTION C
6 Videos
- Additional Practice QuestionsBOOK - CBSE MODEL PAPERCHAPTER - Additional Practice QuestionsEXERCISE - Question
1 Videos
- SAMPLE PAPER 2022 TERM IIBOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022 TERM IIEXERCISE - SECTION B
16 Videos
Similar Questions
Three charges 2q,-q,-q are located at the vertices of an equilateral triangle.At the centre of the triangle (A) The field is zero but potential is non-zero (B) The field is non-zero but potential is zero (C) Both field and potential are zero (D) Both field and potential are non-zero
View SolutionThree charges Q, +q and +q are placed at the vertices of a right-angle isosceles triangle as shown in Fig. The net electrostatic energy of the configuration is zero if Q is equal to :-

View Solution
Knowledge Check
Three Charges 29,- and - lie at vertices of a triangle. The value of E and V at centroid of triangle will be:
AE≠0andV≠0BE=0andV=0CE≠0andV=0DE=0andV≠0Three charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
Athe field is zero but potential is nonzero.Bthe field is nonzero but potential is zero.Cboth field and potential are zero.Dboth field and potential are nonzero.Three charges Q, +q and +q are placed at the vertices of a right angle triangle (isoscles triangle) as shown. The net electrostatic energy of the configuration is zero, if Q is equal to :
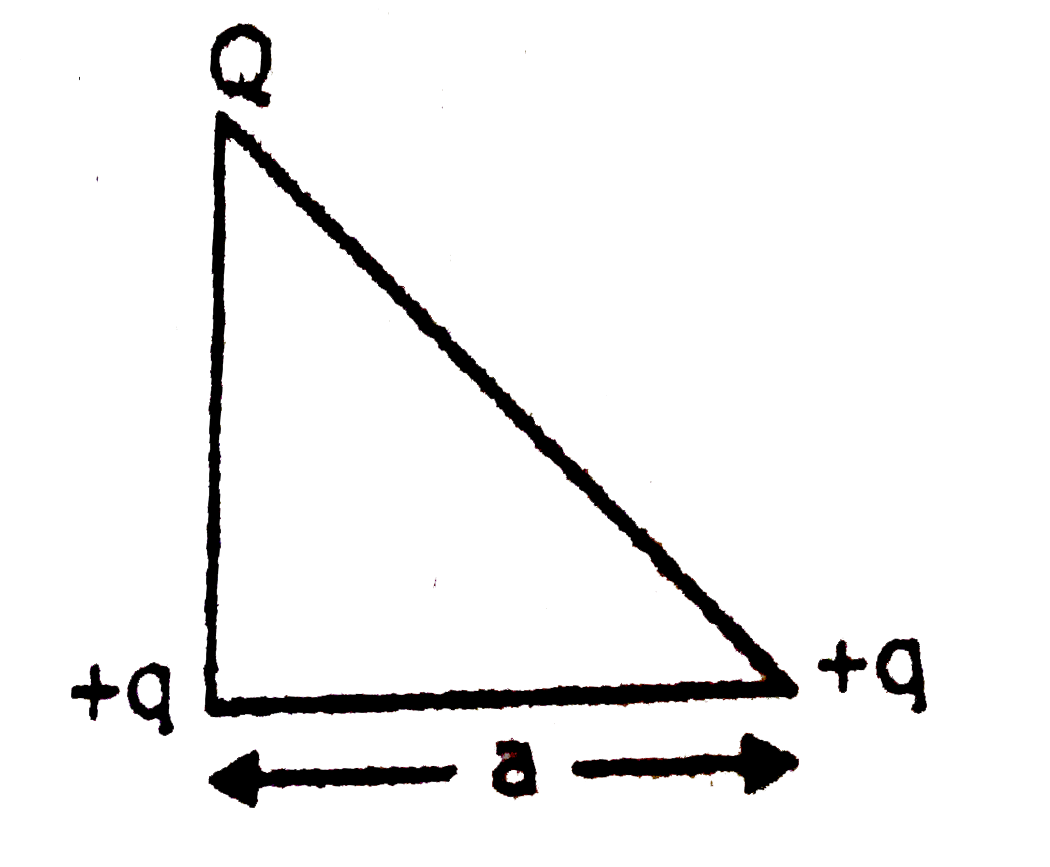 A−q1+√2B−2q2+√2C−2qD+q
A−q1+√2B−2q2+√2C−2qD+q
Three charges Q+q and + q are placed at the vertices of a right -angle isosceles triangle as shown below. The net eletrostatic energy of the configuration is zero if the value of Q is :
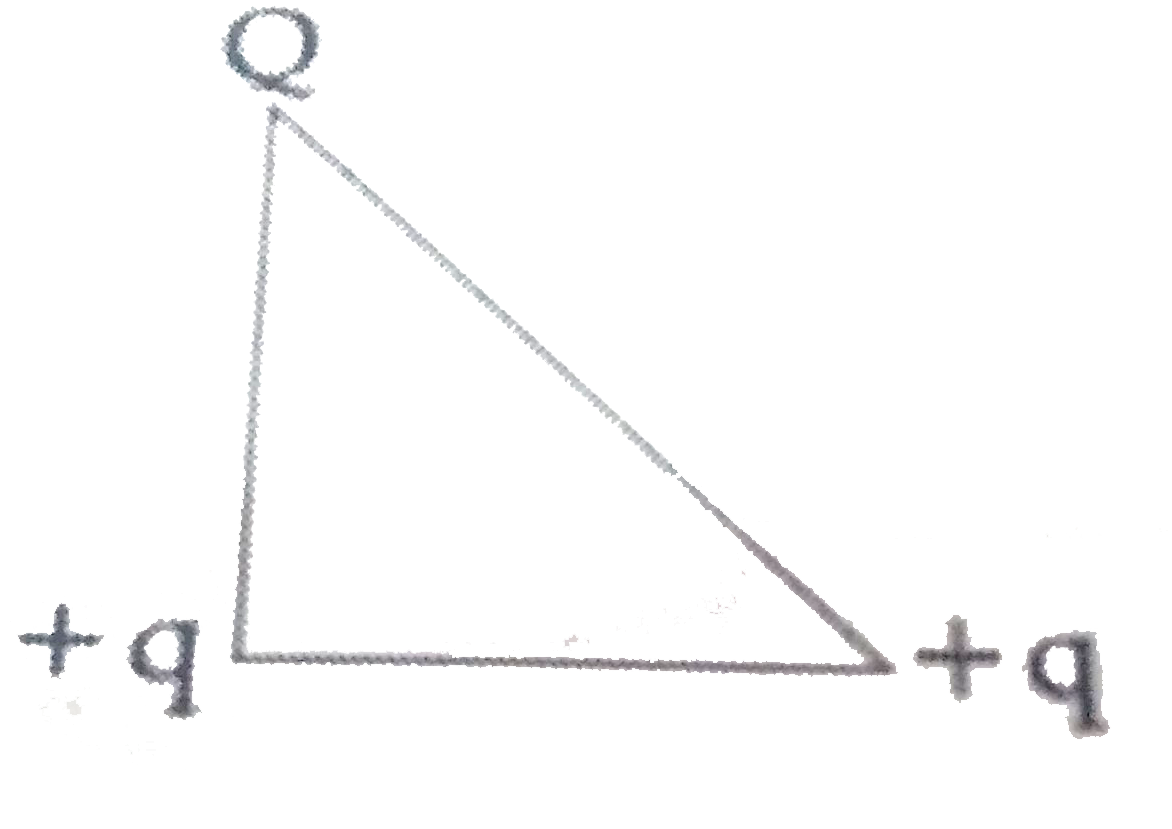
View SolutionConsider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
View SolutionThree charge +q,−q, and +2q are placed at the vertices of a right angled triangle (isosceles triangle)as shown. The net electrostatic energy of the configuration is:

View SolutionThree charges +q, +q and -2q are placed at the vertices of an equilareral triagle. What is the dipole moment of the system?
View SolutionThree charges Q, +q and +q are placed at the vertices of a right-angled isosceles triangle as shown. The net electrostatic energy of the configuration is zero if Q is equal to
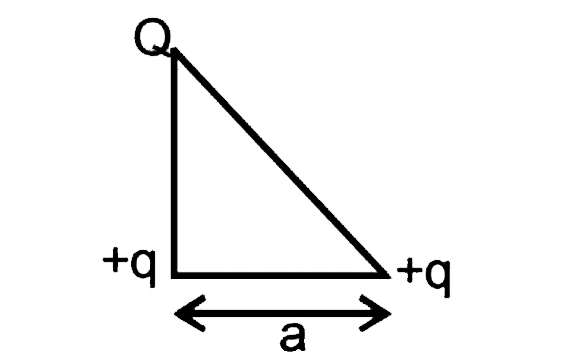
View Solution
