Two parallel plate capacitors X and Y, have the same area of plates and same separation between plates. X has air and Y with dielectric of constant 2 , between its plates. They are connected in series to a battery of 12 V. The ratio of electrostatic energy stored in X and Y is-
4:1
1:4
2:1
1:2
To solve the problem, we need to find the ratio of the electrostatic energy stored in two parallel plate capacitors, X and Y, which are connected in series to a 12 V battery. Capacitor X has air between its plates, while capacitor Y has a dielectric material with a dielectric constant of 2.
1. Understanding the Capacitors:
- Capacitor X (with air): The capacitance CX is given by:
CX=ϵ0Ad
- Capacitor Y (with dielectric constant K=2): The capacitance CY is given by:
CY=K⋅CX=2⋅CX
2. Capacitance Values:
- Let CX=C. Then,
CY=2C
3. Charge on Capacitors:
- When capacitors are connected in series, the charge Q on each capacitor is the same. Therefore,
QX=QY=Q
4. Energy Stored in Capacitors:
- The energy stored in a capacitor is given by the formula:
U=12Q2C
- For capacitor X:
UX=12Q2CX=12Q2C
- For capacitor Y:
UY=12Q2CY=12Q22C=14Q2C
5. Finding the Ratio of Energies:
- Now, we can find the ratio of the energies stored in capacitors X and Y:
UXUY=12Q2C14Q2C=1214=12⋅41=2
6. Final Result:
- Therefore, the ratio of the electrostatic energy stored in capacitors X and Y is:
UXUY=2:1
- Capacitor X (with air): The capacitance CX is given by:
CX=ϵ0Ad
- Capacitor Y (with dielectric constant K=2): The capacitance CY is given by:
CY=K⋅CX=2⋅CX
- Let CX=C. Then,
CY=2C
- When capacitors are connected in series, the charge Q on each capacitor is the same. Therefore,
QX=QY=Q
- The energy stored in a capacitor is given by the formula:
U=12Q2C
- For capacitor X:
UX=12Q2CX=12Q2C
- For capacitor Y:
UY=12Q2CY=12Q22C=14Q2C
- Now, we can find the ratio of the energies stored in capacitors X and Y:
UXUY=12Q2C14Q2C=1214=12⋅41=2
- Therefore, the ratio of the electrostatic energy stored in capacitors X and Y is:
UXUY=2:1
Topper's Solved these Questions
- SAMPLE PAPER 2022BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - SECTION C
6 Videos
- SAMPLE PAPER 2022BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022EXERCISE - SECTION C
6 Videos
- Additional Practice QuestionsBOOK - CBSE MODEL PAPERCHAPTER - Additional Practice QuestionsEXERCISE - Question
1 Videos
- SAMPLE PAPER 2022 TERM IIBOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022 TERM IIEXERCISE - SECTION B
16 Videos
Similar Questions
Two parallel plate capacitors X and Y have the same area of plates and same seperation and air between the plates while Y contains a dielectric medium of ∈r=4

Estimate the ratio of electrostatic energy stored in X and Y.
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same seperation and air between the plates while Y contains a dielectric medium of ∈r=4
Calculate the potential difference between the plates of X and Y.
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same separation between them , X has air between the plates while Y contains a dielectric medium of εr=4.
Estimate the ratio of electrostatic energy stored in X and Y .
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same separation between them , X has air between the plates while Y contains a dielectric medium of εr=4.
Calculate the potential difference between the plates of X and Y.
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same seperation and air between the plates while Y contains a dielectric medium of ∈r=4
Calculate capacitance of capacitor if equivalent of the combind system.
View SolutionTwo parallel palate capacitors X and Y have the same area of plates and same separation between then. X has air between the plates and Y contains a dielectric medium of ∈r=4,
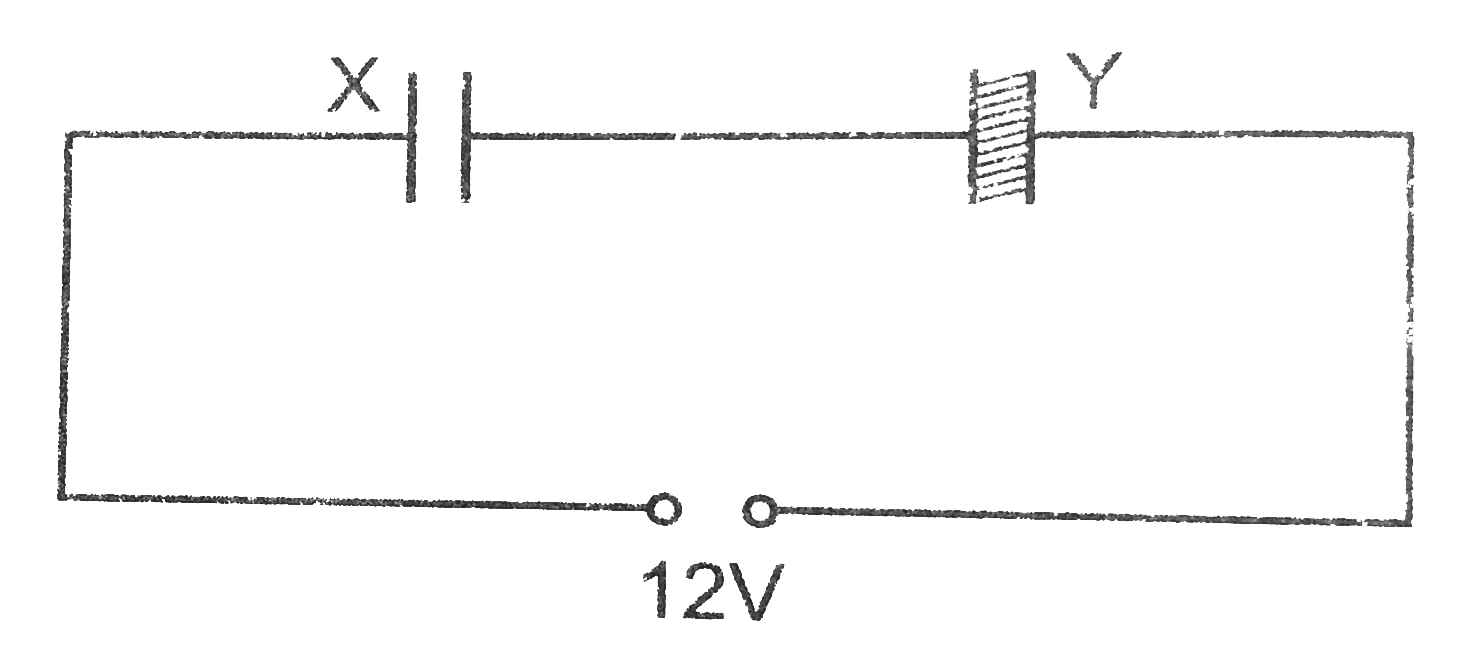
Calculate (i) capacitance of X and Y if equivalent capacitance fo combination is 4μF. (ii) pot diff between the plates of X and Y. (iii) What is the ratio of electrostatic energy stored in X and Y ?
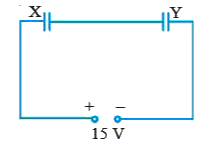
View SolutionTwo parallel plate capacitors X and Y have the same area of the plates and same separation between them, are connected in series to a battery of 15 V. X has air between the plates while Y contains a dielectric of constant k = 2.
Calculate the potential difference between the plates of X and Y.
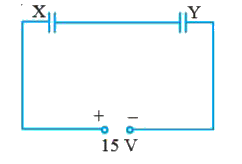
View SolutionTwo parallel plate capacitors X and Y have the same area of the plates and same separation between them, are connected in series to a battery of 15 V. X has air between the plates while Y contains a dielectric of constant k = 2.
Calculate the capacitance of each capacitor if equivalent capacitance of the combination is 2 μF
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same separation between them.
X has air between the plates while Y contains a dielectric medium of er=4
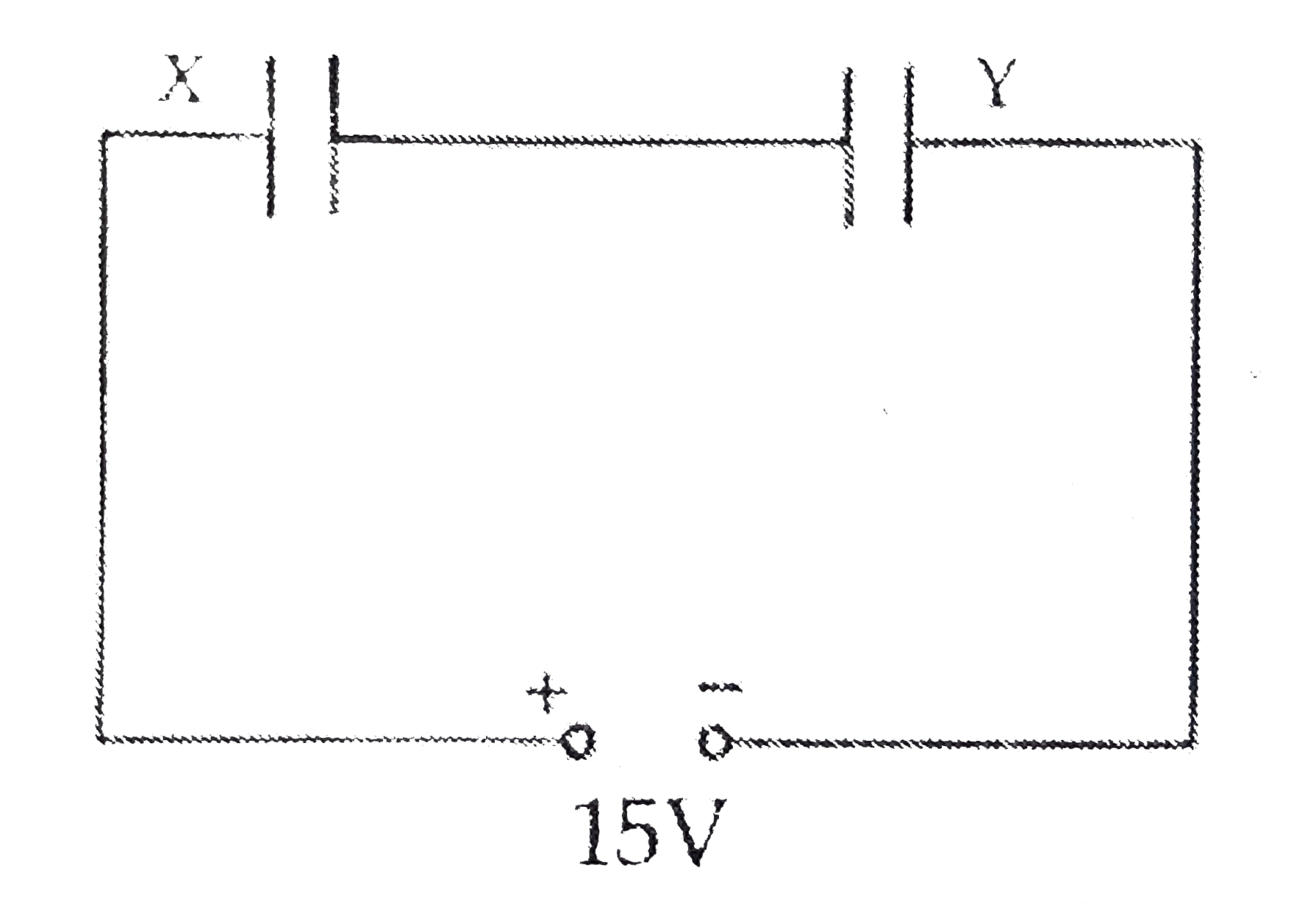
(i) Calculate capacitance of aech capacitor if equivalent capacitance of the combination is 4μF
(ii) Calculate the potential difference between the plates of X and Y
(iii) Estimate the ratio of electrostatic energy stored in X and Y .
View SolutionTwo parallel plate capacitors X and Y have the same area of plates and same separation between them , X has air between the plates while Y contains a dielectric medium of εr=4.
Calculate capacitance of each capacitor if equivalent capacitance of the combination is 4μF.
View Solution
