यदि (1+x)n=C0+C1x+C2x2+.......+Cnxn और 50∑r=0C2r(r+1)=m!(n!)2 है, तो (m +n) का मान बराबर है: (जहां Cr,nCr को निरूपित करता है,)
149
152
155
146
The correct Answer is:B
Step by step video, text & image solution for यदि (1+x)^(n)=C_(0)+C_(1)x+C_(2)x^(2)+.......+C_(n)x^(n) और sum_(r=0)^(50)(C_(r)^(2))/((r+1))=(m!)/((n!)^(2) है, तो (m +n) का मान बराबर है: (जहां C_(r),""^(n)C_(r) को निरूपित करता है,) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
एक यादृच्छिक चर X का प्रायिकता बंटन निम्न रूप में दिया गया है:
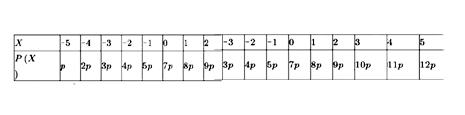
तब, p का मान है04:49View Solutionसमीकरण tan2x−sec10x+1=0 के अंतराल (0, 10) में हलों की संख्या है -
05:03View SolutionIf (1+x)^(n)=sum_(r=0)^(n)C_(r)x^(r) then prove that C_(0)+2C_(1)+3C_(2)+.....+(n+1)C_(n)=2^(n-1)(n+2)
03:14View SolutionIf (1+x)n=n∑r=0Crxr , then prove that C0+C12+.........+Cnn+1=2n+1−1n+1
02:39View SolutionIf m,n,r,∈N then .mC0.nCr+.mC1.nCr−1+……..+.mCr.nC0
= coefficient of xr in (1+x)m(1+x)n
= coefficient of xf in (1+x)m+n
The value of r for which S=.20Cr..10C0+.20Cr−1.10C1+.........20C0.10Cr is maximum can not be05:01View SolutionLet (1+x)n=n∑r=0Crxr and ,
C1C0+2C2C1+C3C2+…+nCnCn−1=1kn(n+1),
then the value of k, is06:14View Solutionthe roots of the equations ∣∣ ∣ ∣∣.xCr.n−1Cr.n−1Cr−1.x+1Cr.nCr.nCr−1.x+2Cr.n+1Cr.n+1Cr−1∣∣ ∣ ∣∣=0
02:58View Solutionयदि (1+x)n=C0+C1x+C2x2+.....+Cnxn. साबित कीजिए कि
C0.Cr+C1.Cr+1+…+Cn−r.Cn=(2n)!(n+r)!(n−1)!05:58View SolutionIf (1+x)n=n∑r=0Crxr,(1+C1C0)(1+C2C1)...(1+CnCn−1) is equal to
04:43View SolutionIf (1+x)n=C0+C1x+C2x2+…and+Cnxn
Σ50r=0C2r(r+1)=m!(n!)2, then the value of (m+n) is equal to (where Cr represents .nCr )View Solutionयदि (1+x)n=n∑r=0Crxr,
(1+C1C0)(1+C2C1)...(1+CnCn−1) का मान है04:25View Solutionयदि (1+x)n=n∑r=0Crxr तो (1+C1C0)(1+C2C1)...(1+CnCn−1)=
05:53View Solutionthe roots of the equations ∣∣ ∣ ∣∣.xCr.n−1Cr.nCr.x+1Cr.nCr.n+1Cr.x+2Cr.n+1Cr.n+2Cr∣∣ ∣ ∣∣=0
02:04View SolutionUse the identity (1+x)m(1+x)n=(1+x)m+n to prove Vandermonde's theorem,
mCr+mCr−1.nC1+mCr−2⋅nC2+….+nCr=(m+n)Cr04:37View SolutionIf (1+x)n=n∑r=0Crxr,(1+C0C1)(1+C2C1)...(1+CnCn−1) is equal to
02:23View SolutionIf m,n,r,∈N then .mC0.nCr+.mC1.nCr−1+……..+.mCr.nC0
= coefficient of xr in (1+x)m(1+x)n
= coefficient of xf in (1+x)m+n
The value of r for which S=.20Cr..10C0+.20Cr−1.10C1+.........20C0.10Cr is maximum can not be06:49View Solution

