दो सीधी सड़कें OA और OB,O पर प्रतिच्छेदन करती है। एक मीनार उनके द्वारा बने कोण के अंदर स्थित है और बिंदु A एवं B जहां सड़कें इससे निकटस्थ है पर 45∘ और 30∘ के कोण अंतरित करती है । यदि OA=100 मीटर और OB=50 मीटर है तब मीनार की ऊंचाई है
25√2 मीटर
50 मीटर
25√6 मीटर
25√3 मीटर
The correct Answer is:C
Step by step video, text & image solution for दो सीधी सड़कें OA और OB,O पर प्रतिच्छेदन करती है। एक मीनार उनके द्वारा बने कोण के अंदर स्थित है और बिंदु A एवं B जहां सड़कें इससे निकटस्थ है पर 45^(@) और 30^(@) के कोण अंतरित करती है । यदि OA=100 मीटर और OB=50 मीटर है तब मीनार की ऊंचाई है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
संख्या (23)14 के अंतिम दो अंक है
03:52View Solutionबहुपद (x−1)(x−2)(x−3)......में ...(x−n)xn−2 का गुणांक है:
04:51View Solutionएक सदिश ¯¯¯¯¯¯OA,OX से 60∘ का कोण बनाता है और OY से 45∘ का कोण बनाता है तथा ∣∣¯¯¯¯¯¯OA∣∣=10 इकाई है। बिंदु A का स्थिति सदिश ज्ञात कीजिए।
05:05View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
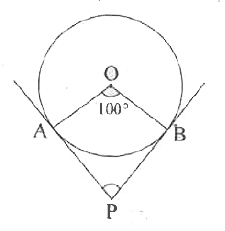 02:36View Solution
02:36View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
02:14View Solutionबिन्दु (1,1) पर वक्रों y=x2 और x=y2 के मध्य कोण है
03:32View SolutionA tower stands on the top of a building which is 40 metres high. The angle of depressiotf of a point situated on the ground-from the top and bottom of the tower are found to Be 60∘ and 45∘ respectively.What is the height (in metres) of tower?
एक भवन जिसकी ऊँचाई 40 मीटर है, के शिखर पर एक मीनार खड़ी है। मीनार के शिखर तथा पांद बिन्दु से भूमि पर स्थित एक बिन्दु का अर्वनमन कोण क्रमशः 60∘ तथा 45∘ है। मीनार की ऊँचाई (मीटर में) क्या है ?01:55View SolutionHeight of a tower is 120 metres. The angle of elevation of the top of tower from a point B is 75^@ .Point B is on the ground level. What is the distance (in metres)of point B from the base of tower? एक भीनार की ऊँचाई 120 मीटर है। बिंदु B से मीनार की चोटी का उन्नयन कोण 75^@ है। बिंदु B जमीन की सतह पर है। मीनार के आधार से बिंदु B की दूरी (मीटर में) क्या है?
03:04View Solutionलेखक और उसकी करती के युग्म गलत है ?
03:43View Solutionअंकित पूर्व दिशा की ओर चलना शुरू करता है | 30 मीटर चलने के बाद वह बाएं मुड़ जाता है और 40 मीटर चलता है फिर वह बाएं मुड़ जाता है और 30 मीटर दूर चलता है | अब वह पुनः बाएं मुड़ता है और 50 मीटर चलता है | तब वह अपनी प्रारम्भिक स्थिति से कितनी दूर है ?
05:24View Solutionएक व्यक्ति पश्चिम दिशा की ओर मूँह करके खड़ा है | वह दक्षिणावर्त दिशा में 45∘ के कोण पर घूमता है फिर वह पुनः उसी दिशा में 180∘ के कोण पर घूमता है और फिर वह वामावर्त दिशा में 270∘ के कोण पर घूमता है | अब वह किस दिशा की ओर खड़ा है ?
02:56View SolutionA and B are two points on a circle with centre O. AT is a tangent, such that angle BAT = 45^@ .N is a point on OA, such that BN= 10 cm. The length of the median OM of the triangle NOB is: A और B केंद्र O वाले एक वृत्त पर स्थित दो बिंदु हैं | AT एक स्पर्श रेखा है जो इस प्रकार है कि angle BAT = 45^@ है| N, OA पर स्थित एक बिंदु है जो इस प्रकार है कि BN =10 सेमी है | triangle NOB की मध्यिका OM की लंबाई ज्ञात करें |
02:27View SolutionIn a circle with centre O, AD is a diameter and AC is a chord. Point B on AC such that OB = 7cm and angle OBA = 60^@ . If angle DOC = 60^@ , then what is the length of BC? केंद्र वाले एक वृत्त में, AD एक व्यास है और AC एक जीवा है। AC पर एक बिंदु B इस प्रकार है की OB = 7 सेमी और angle OBA = 60^@ | यदि angle DOC = 60^@ है, तो BC की लंबाई क्या है?
01:39View SolutionThe angle of elevation of top of a tower from a point P, on the ground is theta such that tan theta =12/5 . If distance of the point P,from the base of the tower is 75m, what is the height of the tower? भूमि पर स्थित एक बिंदु P से किसी मीनार के शीर्ष का उन्नयन कोण theta इस प्रकार है कि tan theta =12/5 है| यदि मीनार के तल से बिंदु P की दूरी 75 मीटर है, तो मीनार की ऊंचाई क्या है ?
02:33View SolutionFrom a point P on a level ground, the angle of elevation of the top of a tower is 30^@ . If the tower is 270 m high, the distance of point P from the foot of the tower is: भूमि पर स्थित किसी बिंदु P से एक मीनार के शीर्ष का उन्नयन कोण 30^@ है | यदि यह मीनार 270 मीटर ऊँची है, तो मीनार के तल से बिंदु P की दूरी ज्ञात करें |
05:27View SolutionFrom the top of a tower, the angles of depression of two objects on the ground on the same side of it, are observed to be 60^@ and 30^@ respectively and the distance between the objects is 400 sqrt3 m. The height (in m) of the tower is : किसी मीनार के शीर्ष से, भूमि पर इसके एक ही तरफ स्थित दो वस्तुओं का अवनमन कोण क्रमशः 60^@ और 30^@ पाया जाता है तथा वस्तुओं के बीच की दूरी 400 sqrt3 मीटर है | इस मीनार की ऊंचाई ( मीटर में ) है
View Solution

