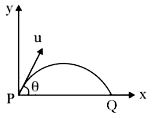
जैसा कि चित्र में दिखाया गया है, द्रव्यमान m, प्रारंभिक चाल हैं और प्रक्षेप कोण θ का एक कण प्रक्षेपित किया जाता है। प्रक्षेपण बिंदु के सापेक्ष प्रारंभिक और अंतिम स्थितियों, P और Q के बीच प्रक्षेप्य पर औसत बलाघूर्ण है:
μ2sin(2θ)2
μ2sin(θ)
μ2cosθ
μ2cosθ2
The correct Answer is:A
→ταv×Δt=Δ→L………(1)
यहाँ, Δt= उड्डयन काल = 2usin(θ)g
∣∣→ΔL∣∣=∣∣→Lf−→Li∣∣ प्रक्षेप के बिंदु के सापेक्ष
=(μsinθ) परास -0
=(μsinθ)(μ2sin2θ)g
∴|→τaV|=ΔLΔt=μ2sinθsin2θg.g2usinθ
=mμ2sin2θ2
Topper's Solved these Questions
Similar Questions
एक नाव 24 km प्रतिप्रवाह और 36 km अनुप्रवाह को 6 घंटे में तय करती है, जबकि यह 36 km प्रतिप्रवाह और 24 km अनुप्रवाह को 612 घंटे में तय करती है। धारा का वेग (kmph में) है:
View Solutionnवी बोर कक्षा में हाइड्रोजन परमाणु इलेक्ट्रॉन के लिए, कक्षा की त्रिज्या और इसकी डी-ब्रोग्ली तरंगदैधर्य का अनुपात है:
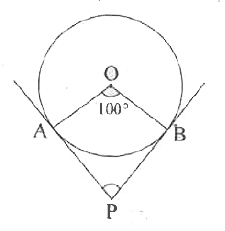
View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
View Solution5 बार और 300K पर एक आदर्श एक्परमाणविक गैस के दो मोल के 1 बार के ब्रह्म डाब तक अनुत्क्रमणीय रूप से प्रसारित किया जाता है गैस दवरा किया गया कार्य xR (बार लीटर में ) है x का मान है
View Solutionसांद्र H2SO4 के साथ गर्म करने पर एल्कोहॉल के एल्फीन में निर्जलीकरण के दौरान प्रारंभिक पद _______ है और इसके बाद ______ क्रियाविधि होती है।
View Solutionरुद्धोष्म और समतापीय स्थितियों के तहत एक आदर्श गैस का उत्क्रमणीय प्रसार चित्र में दिखाया गया है | निम्नलिखित में से कौन सा कथन अशुद्ध है
View Solution298K पर, शुद्ध द्रवों A और B के वाष्प दाब क्रमशः 400 और 600 mm Hg है। दो द्रवों को मिलाने पर, उनके प्रारंभिक आयतन का योग अंतिम मिश्रण के आयतन के बराबर होता हैं मिश्रण में द्रव B का मोल प्रभाज 0.5 हे। अंतिम विलयन का वाष्प दाब, वाष्प प्रावस्था में घटकों A और B के मोल प्रभाज क्रमशः है:
View Solutionएक विलयन को भारानुसार 30% है 200g और भारानुसार 20% के 300g विलयन को मिलाकर प्राप्त किया जाता ह । अंतिम विलयन में विलेय का प्रतिशत क्या है?
View Solutionजब logk और 1/T के बीच एक आलेख आलेखित किया जाता है, तो हमें एक आलेख प्राप्त होता है, जैसा कि नीचे दर्शाया गया है आलेख में ढाल का मान क्या है?
View Solutionकैल्सियम क्लोराइड और सोडियम क्लोराइड के मिश्रण का 10.0 ग्राम प्रतिदर्श Na2CO3 के साथ कैल्सियम कार्बोनेट के रूप में कैल्सियम को अवक्षेपित करने के लिए उपचारित किया जाता है ।यह CaCO3 सभी केल्सिूयम को CaO में परिवर्तित करने के लिए गरम किया जाता है और CaO का अंतिम द्रव्यमान 1.62 ग्राम है। प्रारंभिक मिश्रण में CaCl2 के द्रव्यमान क्या % था?
View Solutionप्रथम कोटि अभिक्रिया के लिए निम्नलिखित में से कौन सा सही है/हैं? (a अभिकारक की प्रारंभिक सांद्रता है, x अभिकृत अभिकारक की सांद्रता है और t समय है)
View Solutionजलीय विलयन में FeCl3,K4[Fe(CN)6] के साथ अभिक्रिया करने पर नीला रंग देता है। ये एक अर्धपारगम्य झिल्ली AB द्वारा अलग किए जाते हैं जैसा कि चित्र में दिखाया गया है। परासरण के कारण

View Solutionप्रारंभ में STP पर एक आदर्श गैस (C_(V)=20JK^(-1)mol^(-1)) का एक मोल प्रारंभिक ताप में दोगुना होने तक नियत आयतन पर गर्म किया जाता है | प्रक्रम के लिए W और q होगा-
View Solutionएक यौगिक AB में, A और B के बीच विद्युत् ऋणता का अंतर 1.9 है। A और B की परमाणु त्रिज्या 4Å और 2Å हैं। A और B परमाणुओं के बीच की दूरी अर्थात dA−B है
View Solution298 K पर शुद्ध द्रवों, A और B के वाष्प दाब क्रमश: 400 और 600 mm Hg हैं। इन दो द्रों को मिश्रित करने पर, उनके प्रारंभिक आयतनों का योगफल अंतिम मिश्रण के आयतन के बराबर होता है। मिश्रण में द्रव B का मोल प्रभाज 0.5 है। अंतिम विलयन का वाष्प दाब और वाष्प प्रावस्था में A और B घटों के मोल प्रभाज क्रमशः हैं
View Solutionएक गैस को इस तरह गर्म किया जाता है कि उसका दाब और आयतन दोनों दोगुने हो जाते हैं। तब ताप में कमी करके वायु के कुछ अणुओं को पात्र में मिलाया जाता है ताकि दोगुने किये गए आयतन और दाब को बनाये रखा जा सके। माना कि प्रारंभिक मोलों की संख्या के 1वें भाग को इस उद्देश्य के लिए मिलाया गया है। तब प्रारंभिक परमताप के सापेक्ष परिणामी ताप का प्रभाज क्या होगा?
View Solution
