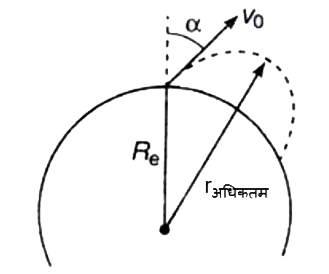
पृथ्वी के पृष्ठ से द्रव्यमान m का एक प्रक्षेप्य ऊर्ध्वाधर से कोण a = 60° पर दागा जाता है। प्रारंभिक चाल $v_{0}, \sqrt{\frac{G M_{e}}{R_{e}}}$ के बराबर है। पृथ्वी की पृष्ठ से अधिकतम ऊंचाई जहाँ तक प्रक्षेप्य ऊपर उठ सकता है, $\frac{R_{e}}{x}$ का मान ज्ञात कीजिए?
G = सार्वत्रिक गुरुत्वाकर्षण स्थिरांक
$M_{e}$ = पृथ्वी का द्रव्यमान
$R_{e}$ = पृथ्वी का त्रिज्या

Text Solution

Verified by Experts

The correct Answer is:B

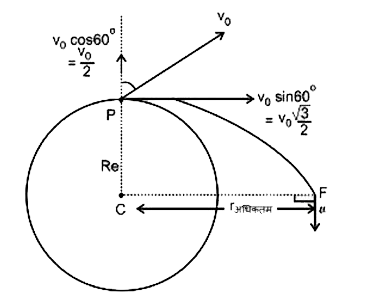
C के परितः P और F पर कोणीय संवेग के संरक्षण द्वारा,
$m v_{0} \frac{\sqrt{3}}{2} R (e) = m v r$
$\Rightarrow v = \frac{\sqrt{3} R_{e} v_{0}}{2 r_{अधिकतम}}$ ................(i)
P और F के बीच यांत्रिक ऊर्जा के संरक्षण द्वारा,
$\frac{1}{2} m v_{0}^{2} - \frac{G M_{e} m}{R_{e}} = \frac{1}{2} m v^{2} - \frac{G M_{e} m}{r_{अधिकतम}}$ .............(ii)
समीकरण (i) को समीकरण (ii) में रखिए,
$\frac{1}{2} m v_{0}^{2} - \frac{G M_{e} m}{R_{e}} = \frac{1}{2} m \frac{3 R^{2} v_{0}^{2}}{4 r_{अधिकतम}^{2}} - \frac{G M_{e} m}{r_{अधिकतम}}$
$v_{0} = \sqrt{\frac{G M_{e}}{R}}$
$\Rightarrow \frac{1}{2 R_{e}} - \frac{1}{R_{e}} = \frac{3 R}{8 r_{अधिकतम}^{2}} - \frac{1}{r_{अधिकतम}}$
$\Rightarrow - \frac{1}{2 R_{e}} = \frac{3 R_{e} - 8 r_{अधिकतम}}{8 r_{अधिकतम}^{2}}$
$\Rightarrow 4 r_{अधिकतम}^{2} - 8 R_{e} r_{अधिकतम} + 3 R_{e}^{2} = 0$
द्विघात समीकरण को $r_{अधिकतम}$ में हल करने पर, हमें प्राप्त होता है,
$r_{अधिकतम} = \frac{8 R_{e} \pm \sqrt{16} R_{e}}{8} = \frac{8 R_{e} \pm 4 R_{e}}{8}$
$\Rightarrow r_{अधिकतम} = \frac{8 R_{e} + 4 R_{e}}{8} = \frac{12 R_{e}}{8} = \frac{3 R_{e}}{2}$
$∴ h_{अधिकतम} = r_{अधिकतम} - R_{e} = \frac{3 R_{e}}{2} - R_{e} = \frac{R_{e}}{2}$
$∴ X = 2$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

NTA MOCK TESTS-JEE MAIN TEST-59-भौतिक विज्ञान

Home
Ask Doubt
Profile