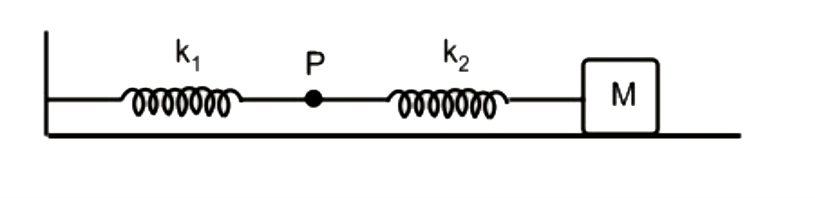
चित्र में दिखाया गया द्रव्यमान M आयाम A के साथ सरल आवर्त गति में दोलन करता है। बिंदु P का आयाम है

A

$\frac{k_{1} A}{k_{2}}$

B

$\frac{k_{2} A}{k_{2} - k_{1}}$

C

$\frac{k_{2} A}{k_{1} + k_{2}}$

D

$\frac{k_{2} A}{k_{1}}$

Text Solution

Verified by Experts

The correct Answer is:C

मान लीजि दाईं ओर यदि M पर कोई बल F अनुप्रयुक्त किया जाता है तो माना कि M द्वारा तय की गई दूरी A है। यदि निकाय को छोड़ा जाता है तो यह आयाम A की सरल आवर्त गति करता है। यदि $A_{1}$ और $A_{2}$ स्‍प्रिंग $k_{1}$ और $k_{2}$ में विस्तार है तब $A = (A_{1} + A_{2})$ और
$F = k_{1} A_{1} = k_{2} A_{2}$
$\Rightarrow A_{1} = \frac{F}{k_{1}}$ और $A_{2} = \frac{F}{k_{2}}$
$∴ A = A_{1} + A_{2} = F (\frac{1}{k_{1}} + \frac{1}{k_{2}})$
$= \frac{F (k_{1} + k_{2})}{k_{1} k_{2}}$
बिंदु P का आयाम = स्‍प्रिंग $k_{1}$ के दोलन का आयाम जो है
$A_{1} = \frac{F}{k_{1}} = \frac{k_{2} A}{(k_{1} + k_{2})}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

NTA MOCK TESTS-JEE MAIN TEST 76-भौतिक विज्ञान

Home
Ask Doubt
Profile