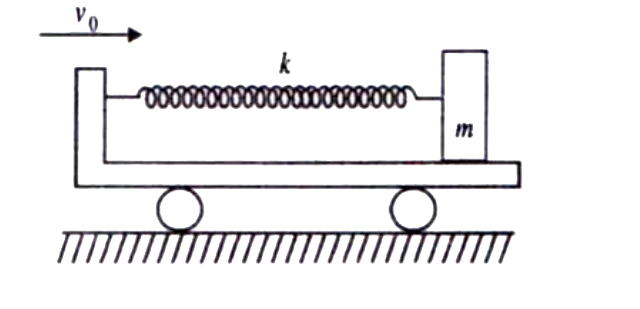
द्रव्यमान m का एक गुटका एक हल्की स्प्रिंग द्वारा जिसकी दृढ़ता k है है एक चिकनी वेज (तख्ते) के साथ दृढ़ता से जुड़ा हुआ है। यदि वेज को नियत वेग से गति कराई जाती है तो स्प्रिंग के अधिकतम संपीडन तक बाह्य कारक द्वारा किया गया कार्य ज्ञात कीजिए।
The correct Answer is:A
आइए हम वेज+सिप्रंग +गुटका को एक निकाय के रूप में लें। कार्य करने के लिए जिम्मेदार बल स्प्रिंग बल और बाह्य बल है।
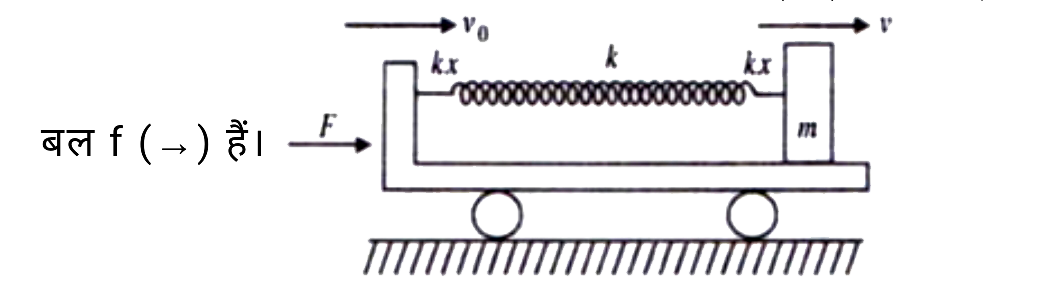
धरातल के सापेक्ष गुटके+सिप्रंग +तख्ते के लिए कार्य ऊर्जा प्रमेय
कार्य ऊर्जा प्रमें को लागू करने के लिए हमारे पास है
जहां सिप्रंग द्वारा वेज और गुटके पर किया गया कुल कार्य है और गुटके की गतिज ऊर्जा में परिवर्तन है (क्योंकि तख्ता अपनी गतिज ऊर्जा में परिवर्तन नही करता है)
तब
क्योंकि गुटका शुरू में स्थिर था और यह सिप्रंग के अधिकतम संपीडन के समय तख्ते के बराबर वेग प्राप्त करेगा। धरातल के सापेक्ष गुटके की गतिज ऊर्जा में परिवर्तन
उपरोक्त समीकरण में को प्रतिस्थापित करने पर हमारे पास है
.....i
तख्ते के सापेक्ष गुटके+स्प्रिंग +तख्ते के लिए कार्य ऊर्जा प्रमेय
तख्ता नियत वेग से गति करता है गुटके पर कोई छद्म बल काम नही करता है।
, तब सिप्रंग द्वारा निकाय (गुटका+तख्ता) पर किया गया कुल कार्य निम्न द्वारा दिया जा सकता है:
क्योंकि स्प्रिंग के अधिकतम संपीडन के समय गुटके और प्रेक्षक (तख्ता) के बीच आपेक्षित वेग से शून्य तक कम हो जाता है तब गुटके की गतिज ऊर्जा में परिवर्तन है।
उपरोक्त समीकरण में और का मान रखने पर
......ii
(i) और (ii) से
Topper's Solved these Questions
Similar Questions
एक प्रोटॉन से बने एक परमाणु और इलेक्ट्रॉन के समान आवेश लेकिन दोगुने द्रव्यमान के काल्पनिक कण की कल्पना कीजिए। बोर परमाणु मॉडल को लागू कीजिए और प्रथम उत्तेजित स्तर पर इस काल्पनिक कण के सभी संभव संक्रमण पर विचार कीजिए। उत्सर्जित होने वाले सबसे लंबे तरंगदैर्ध्य वाले फोटॉन की तरंगदैर्ध्य x (हाइड्रोजन परमाणु के लिए रिडबर्ग स्थिरांक R के पदों में दिया गया है) बराबर है:
View Solutionयदि हाइड्रोजन परमाणु की लाइमैन श्रेणी की श्रेणी सीमा तरंगदैर्ध्य 912 Å है, तब हाइड्रोजन परमाणु की बामर श्रेणी की श्रेणी सीमा तरंगदैर्ध्य है:
View Solutionएक सरल रेखा बिन्दु (-1,5) से होकर जाती है और रेखा द्वारा अक्षो के बीच काटे हुए भाग को यह बिन्दु 3:2 के अनुपात में विभाजित करता है। रेखा का समीकरण ज्ञात कीजिए|
View Solutionएक अनभिनत पासे को 5 बार उछाला जाता है एक समसंख्या प्राप्त करना एक सफलता है तो प्रायिकता ज्ञात कीजिए - अधिक से अधिक 4 सफलताओ के लिए
View Solutionएक अनभिनत पास को 6 बार उछाला जाता है। यदि एक समसंख्या प्राप्त करना एक सफलता है , तो
अधिक - से - अधिक 5 सफलताओ की प्रायिकता ज्ञात कीजिए।
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionकार्य || एक नियत बल द्वारा किया गया कार्य।
View Solutionएक्जाम स्पेशल |एक नियत बल द्वारा किया गया कार्य
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View Solutionएक रेखा की दिक्-कोसाइन ज्ञात कीजिए तो निर्देशांक्षो के साथ समान कोण बनाती है |
View Solutionएक 5 kg द्रव्यमान वाली वस्तु पर 2s के लिये एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3m/s से बढा 7m/s कर देता है। लगाये गये बल की मात्रा ज्ञात करें
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solutionजब एक समदाबीय प्रक्रम में, गैस X को 5000 कैलोरी ऊष्मा प्रदान की जाती है, तो इसके द्वारा किया गया कार्य 142.8 कैलोरी होता है | गैस X होगी :
View Solution5 बार और 300 K पर एक आदर्श एकलपरमाण्विक गैस के दो मोल को 0.5 बार के बाह्य दाब के विरुद्ध 1 बार और 240 K के अंतिम दाब तक अनुत्क्रमणीय रूप से प्रसारित किया जाता है। गैस द्वारा किया गया कार्य –xR है। x का मान है: (यहाँ R गैस स्थिरांक है)
View Solution5 बार और 300K पर एक आदर्श एक्परमाणविक गैस के दो मोल के 1 बार के ब्रह्म डाब तक अनुत्क्रमणीय रूप से प्रसारित किया जाता है गैस दवरा किया गया कार्य xR (बार लीटर में ) है x का मान है
View SolutionNaCl के संकुलन प्रभाज के लिए निम्नलिखित में से कौन सा व्यंजक सही है, यदि एक फलक और एक विकर्ण से a- आयन को हटा दिया जाता है?
View Solution
