बिंदु B की ऊंचाई है
(3√3m)tan30∘=(3√3m)(1√3)
=3m
B पर गुटके की ऊर्जा है
KE+PE=12M(√45ms−1)2
+Mg(3m)
C पर गुटके के ऊर्जा है
KE=12MV2
ऊर्जा संरक्षण के सिद्धांत देता है
12MV2=12M(√45ms−1)2
+M(10ms−2)(3m)
यह देता है V=√105ms−1
इसलिए विकल्प (√105ms−1) सही है।3Ω प्रतिरोध के धातु के एक तार को उसकी पिछली लंबाई के दोगुनी लंबाई का एक समान तार बनाने के लिए खींचा जाता है। इस नए तार के दोनों सिरों को एक वृत्त बनाने के लिए मोड़ा जाता है। यदि इस वृत्त पर दो बिंदु इसके केंद्र पर 60∘ का कोण बनाते हैं तब इन दो बिंदुओं के बीच का तुल्य प्रतिरोध होगा:
A
53Ω
B
125Ω
C
72Ω
D
52Ω
Text Solution
The correct Answer is:A
हम जानते हैं R=8lA=8l2Al=8l2आयतन
यदि आयतन स्थिर है तब R∝l2
∴ नया प्रतिरोध =4R
R2=4R360×300
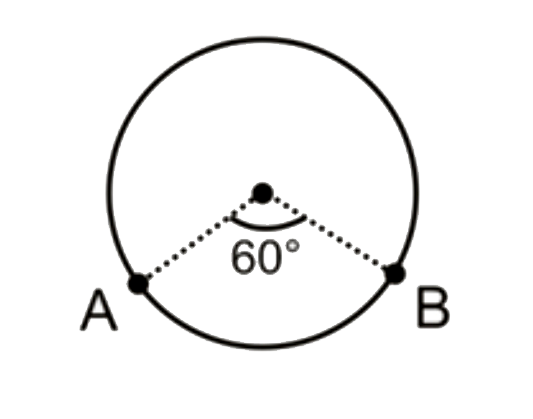
R1=4r360×60
R1=4R360×300=10R3
R2=4R360×60=2R3
∴तुल्य प्रतिरोध R_("तुल्य")=(R_(1)R_(2))/(R_(1)+R_(2))
=10R3×2R310R3+2R3=5R9
=53Ω
|
