आरेख में दिखाए गए बोर्ड और फर्श के बीच घर्षण गुणांक μ है। अधिकतम बल ज्ञात कीजिए जो आदमी, रस्सी पर लगा सकता है, ताकि बोर्ड फर्श पर न फिसले।

μ(m+M)g(2+μ)
μ(m+M)g(1+μ)
μ(m+M)g(2−μ)
μ(m+M)g(1−μ)
The correct Answer is:B
निकाय पर कार्य करने वाले बलों को आरेख में दिखाया गया है
बिंदु P के ऊर्ध्वाधर साम्यावस्था के लिए
T=F …(i)
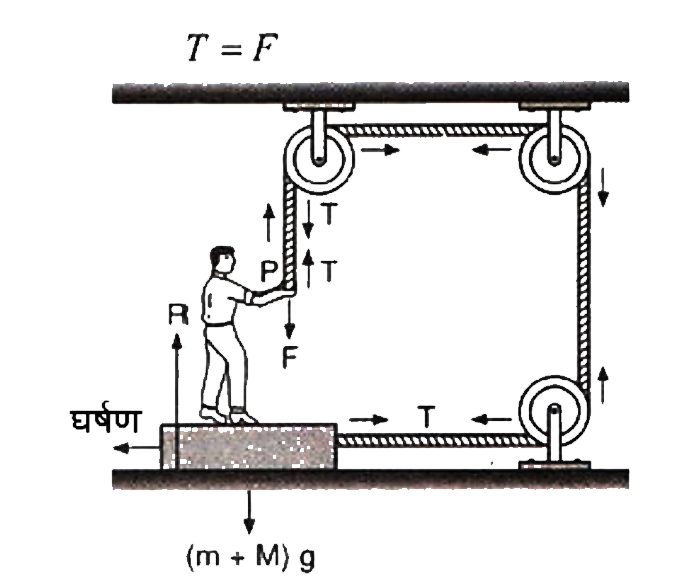
और निकाय की ऊर्ध्वाधर साम्यावस्था के लिए
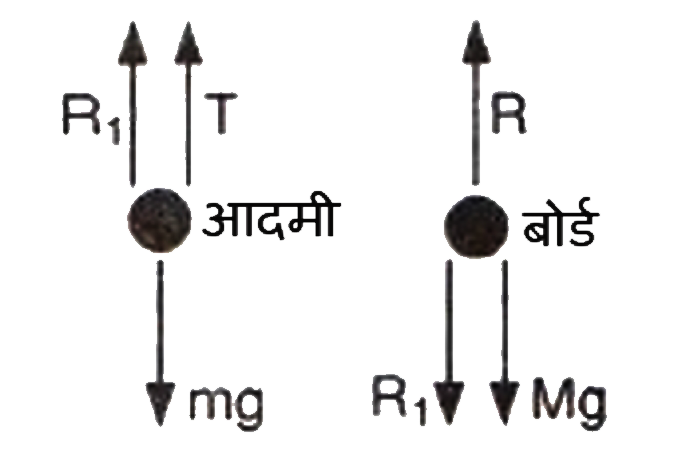
R + T = (m + M)g, अर्थात,
R=(m+M)g−T ....(ii)
अब निकाय क्षैतिज रूप से तब तक नहीं गति करेगा, जब तक
T<fL
अर्थात T<μ[(m+M)g−T]
(fL=μR)
जो सरलीकरण करने पर, देता है
T<μ(m+M)g(1+μ)
इसलिए समीकरण (i) के प्रकाश में, हम प्राप्त करते है
Fmax=μ(m+M)g(1+μ)
Topper's Solved these Questions
Similar Questions
निम्नलिखित में से किस संक्रमण के दौरान अधिकतम ऊर्जा मुक्त होती है?
View Solutionएक स्प्रिंग-द्रव्यमान निकाय का आवर्त काल T है। यदि इस स्प्रिंग को दो भागों में काट दिया जाता है जिसकी लम्बाईयाँ 1:3 के अनुपात में है, और समान द्रव्यमान को लंबे भाग से जोड़ा जाता है, तो नया आवर्त काल होगा:
View Solutionचित्र में प्रदर्शित ब्लॉकों के बीच घर्षण गुणांक μ है, किन्तु फर्श घर्षणरहित है|
View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
View Solutionउन सरल रेखाओ के समीकरण ज्ञात कीजिए जो :
x=3 तथा x=−3 से समान दूरी पर है
View Solutionउन सरल रेखाओ के समीकरण ज्ञात कीजिए जो :
y=−5 तथा y=1 से समान दूरी पर है
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solutionएक छोटी फर्म सोने के अंगूठियां और चेनों का निर्माण करती है| प्रतिदिन अंगूठियों और चेनों के निर्माण की कुल संख्या अधिकतम 24 है| एक अंगूठी बनाने में एक घंटा तथा के चेन के बनाने में 30 मिनट लगते है| प्रतिदिन उपलब्ध घंटों की अधिकतम संख्या 16 है|यदि अंगूठी पर लाभ रु 300 तथा एक चेन पर लाभ रु 190 हो, तो ज्ञात कीजिए| की प्रतिदिन कितनी अंगूठियों और चेनों का निर्माण किया जाय ताकि अधिकतम लाभ कमाया जा सकें|
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionचित्र में दिखाए गए छायांकित क्षेत्र के लिए असामिका है-
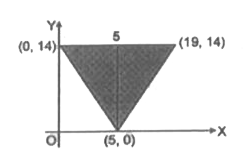
View Solutionबिंदुओं (3,1) और (0,y) के बीच की दूरी 5 है। y ज्ञात कीजिए।
View Solutionएक बिन्दु पर क्रियाशील दो बल P और Q का अधिकतम परिणामी बल ........ होता है।
View Solutionयू.पी. बोर्ड स्पेशल (आर्यभट्ट Revision Series)|समीकरणों के हल पर आधारित बोर्ड परीक्षा में आये हुए प्रश्नों पर चर्चा
View Solutionबोर्ड स्पेशल |द्विघात समीकरण का Revision #!#बोर्ड में पूछे गए सवालों पर चर्चा
View Solutionबोर्ड के लिए महत्वपूर्ण प्रश्नों पर चर्चा
View Solutionपाइथागोरस प्रमेय पर बोर्ड परीक्षा में पूछे गए प्रश्न
View Solution
