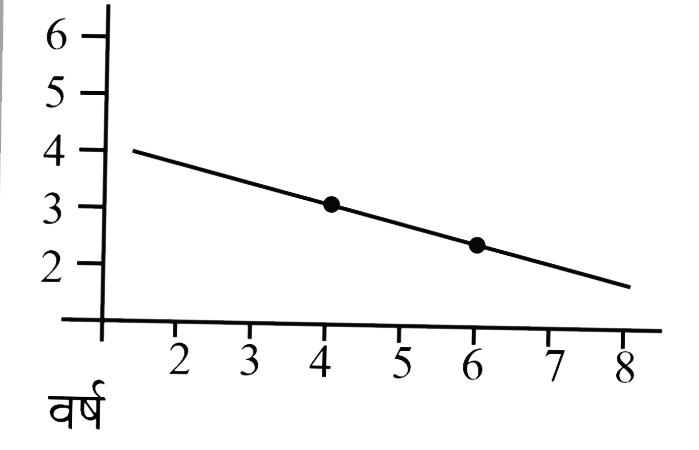
एक रेडियोधर्मी तत्व की अर्द्ध आयु ज्ञात करने के लिए, एक छात्र ln∣∣∣dN(t)dt∣∣∣ बनाम t का आलेख खींचता है। यहाँ dN(t)dt , समय t पर रेडियोधर्मी क्षय की दर है। यदि 4. 16 वर्ष बाद इस तत्व के रेडियोधर्मी नाभिकों की संख्या p के गुणक से घटती है, तब p का मान है: ( e−2.08=0.125)
The correct Answer is:8
∣∣∣dNdt∣∣∣ रेडियोधर्मी पदार्थ की सक्रियता
=λN=λN0e−λt(∴N=N0e−λt)
दोनों ओर लघुगुणक लेने पर,
ln∣∣∣dNdt∣∣∣=ln(λN0)−λt
अतः In∣∣∣dNdt∣∣∣ बनाम t आलेख प्रवणता −λ की एक सरल रेखा है।
आलेख से, हम देख सकते हैं कि,
λ=12=0.5 वर्ष−1
अब समीकरण लागू करने पर,
N=N0eλt=N0e−0.5×4.16
=N0e−2.08=N0e−2×(0.693)=0.125N0
=N08
अर्थात नाभिक 8 के गुणक से घटते हैं।
अतः उत्तर 8 है।
Topper's Solved these Questions
Similar Questions
निम्नलिखित में से किस संक्रमण के दौरान अधिकतम ऊर्जा मुक्त होती है?
View Solutionएक स्प्रिंग-द्रव्यमान निकाय का आवर्त काल T है। यदि इस स्प्रिंग को दो भागों में काट दिया जाता है जिसकी लम्बाईयाँ 1:3 के अनुपात में है, और समान द्रव्यमान को लंबे भाग से जोड़ा जाता है, तो नया आवर्त काल होगा:
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionयदि पिता एवं पुत्र की आयु का योग (वर्षो में) 65 है तथा उनकी आयु के अन्तर का दुगुना 50 वर्ष है तब पिता की आयु होगी -
View Solutionएक रेडियो सक्रिय पदार्थ का 16g, 1घंटे के बाद 0.5 g तक कम हो जाता है। रेडियोधर्मी पदार्थ की अर्थ आयु मिनट में है:
View Solutionनाभिक से दूरी पर, अनंतसूक्ष्म मोटाई dr के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4rr2 dr है। r पर P की निर्भरता का गुणात्मक रेखाचित्र है-
View Solutionएक एंजाइम उत्प्रेरित अभिक्रिया के लिए, ताप (T) के सापेक्ष अभिक्रिया की दर (r) को आलेखित किया गया है। निम्नलिखित में से कौन सा सही निरूपण है?
View Solutionएक रेडियोधर्मी समस्थानिक की अर्द्ध आयु तीन घंटे है। यदि समस्थानिक का प्रारंभिक द्रव्यमान 256 g था, तो 18 घंटे के बाद इसका शेष अक्षयित द्रव्यमान (ग्राम में) होगा:
View Solutionजब गैस को जल के माध्यम से 298K पर बुदबुदाया जाता है, तब गैस का एक तनु विलयन प्राप्त होता है। गैस के लिए हेनरी स्थिरांक 100 Kbar है। यदि गैस 1 बार का दाब डालती है, तो 1 लीटर जल में विलीन गैस के मोलो की संख्या x×10−5 है। यहाँ x का मान ज्ञात कीजिए?
View Solutionप्रथम कोटि अभिक्रिया के लिए निम्नलिखित में से कौन सा सही है/हैं? (a अभिकारक की प्रारंभिक सांद्रता है, x अभिकृत अभिकारक की सांद्रता है और t समय है)
View Solutionसिरोटोनिन एक प्रसिद्ध प्रशान्तक है। यदि इसमें एकाकी युग्म इलेक्ट्रॉनों की संख्या 'X' और T -बंधों की संख्या 'Y' है, तो x + Y का योगफल किसके बराबर है :
View Solutionउच्च तापमान पर एक साम्यावस्था क्रियाकारकां की ओर विस्थापित हो जाती है इस साम्यावस्था के लिए In K तथा 1//T के मध्य कौन सा आलेख सही है?
View Solutionप्रथम कोटि की अभिक्रिया के लिए, यदि 50% अभिक्रिया पूर्ण होने में लगने वाला समय '' सेकंड है, तब 99.9% अभिक्रिया पूर्ण होने के लिए आवश्यक समय n 't' है। n का मान ज्ञात कीजिए?
View Solutionसक्रियण ऊर्जा की गणना के लिए log k बनाम 1/T के बीच का आरेख किसके द्वारा दिखाया गया है?
View Solutionठोस पर, एक गैस के अधिशोषण के लिए, log (x/m) और log P का आलेख रेखिक है, जिसकी ढाल है: (n पूर्णांक संख्या है)
View Solution""_ZX^A के रेडियोधर्मी क्षय में, निम्नलिखित में से किसे अशुद्ध कथन के रूप में माना जा सकता है?
View Solution
