A mass of 10kg is suspended vertically by a rope of length 5 m from the roof. A force of 30 N is applied at the middle point of rope in horizontal direction .The angle made by upper half of the rope with vertical is θ=tan−1(x×10−1). The value of x is _______
(Given , g =10m/s2)
The correct Answer is:0.3
To solve the problem, we need to analyze the forces acting on the mass suspended by the rope and the effect of the horizontal force applied at the midpoint of the rope.
1. Identify the Forces:
- The mass m=10kg exerts a downward force due to gravity, which is mg=10×10=100N.
- A horizontal force F=30N is applied at the midpoint of the rope.
2. Set Up the Geometry:
- The rope has a total length of L=5m. The midpoint is at 2.5m.
- The angle θ is formed by the upper half of the rope with the vertical.
3. Equilibrium Conditions:
- For the horizontal direction, the tension component must balance the applied force:
Tsinθ=F
- For the vertical direction, the tension component must balance the weight of the mass:
Tcosθ=mg
4. Substituting Known Values:
- From the vertical equilibrium equation:
Tcosθ=100(1)
- From the horizontal equilibrium equation:
Tsinθ=30(2)
5. Dividing the Equations:
- Divide equation (2) by equation (1):
TsinθTcosθ=30100
- This simplifies to:
tanθ=30100=310
6. Finding θ:
- We know that θ=tan−1(310).
7. Relating to the Given Equation:
- The problem states that θ=tan−1(x10).
- Therefore, we can equate:
x10=310
8. Solving for x:
- Multiply both sides by 10:
x=3
Final Answer:
The value of x is 3.
- The mass m=10kg exerts a downward force due to gravity, which is mg=10×10=100N.
- A horizontal force F=30N is applied at the midpoint of the rope.
- The rope has a total length of L=5m. The midpoint is at 2.5m.
- The angle θ is formed by the upper half of the rope with the vertical.
- For the horizontal direction, the tension component must balance the applied force:
Tsinθ=F
- For the vertical direction, the tension component must balance the weight of the mass:
Tcosθ=mg
- From the vertical equilibrium equation:
Tcosθ=100(1)
- From the horizontal equilibrium equation:
Tsinθ=30(2)
- Divide equation (2) by equation (1):
TsinθTcosθ=30100
- This simplifies to:
tanθ=30100=310
- We know that θ=tan−1(310).
- The problem states that θ=tan−1(x10).
- Therefore, we can equate:
x10=310
- Multiply both sides by 10:
x=3
The value of x is 3.
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -A)
20 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
A mass of 10 kg is suspended vertically by a rope of length 2 m from a ceiling. A force of 60 N is applied at the middle point of the rope in the horizontal direction, as shown in Fig. Calculate the angle the rope makes with the vertical. Neglect the mass of the rope and take g=10ms−2.

View SolutionA mass of 6 kg is suspended by a rope of length 2 m from the ceilling A force of 50 N in the horizontal direction is applied at the mid - point P of the rope as shown . What is the angle the rope makes with the vertical in equilibrium ? (Take = 10ms−2) . Neglect mass of the rope .
View Solution
Knowledge Check
A mass of 10 kg is suspended by a rope of length 2.8m from a ceiling. A force of 98 N is applied at the midpoint of the rope as shown in figure. The angle which the rope makes with the vertical in equilibrium is
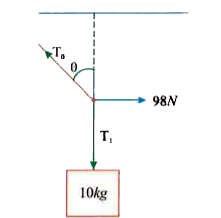 A30∘B60∘C45∘D90∘
A30∘B60∘C45∘D90∘A mass of 20 kg is suspended by a rope of length 4 m from the ceiling. A force of 60 N is applied at the midpoint of the rope in the horizontal direction. What is the angle made by the rope with the vertical in equilibrium? Assume that the mass of the rope is negligible and g=10m/s2
Aθ=tan−1(110)Bθ=tan−1(15)Cθ=tan−1(310)Dθ=tan−1(12)A mass of 10kg is suspended by a rope of length 2.8m from a ceiling. A force of 98N is applied at the midpoint of the rope as shown in figure. The angle which the rope makes with the vertical in equilibrium is
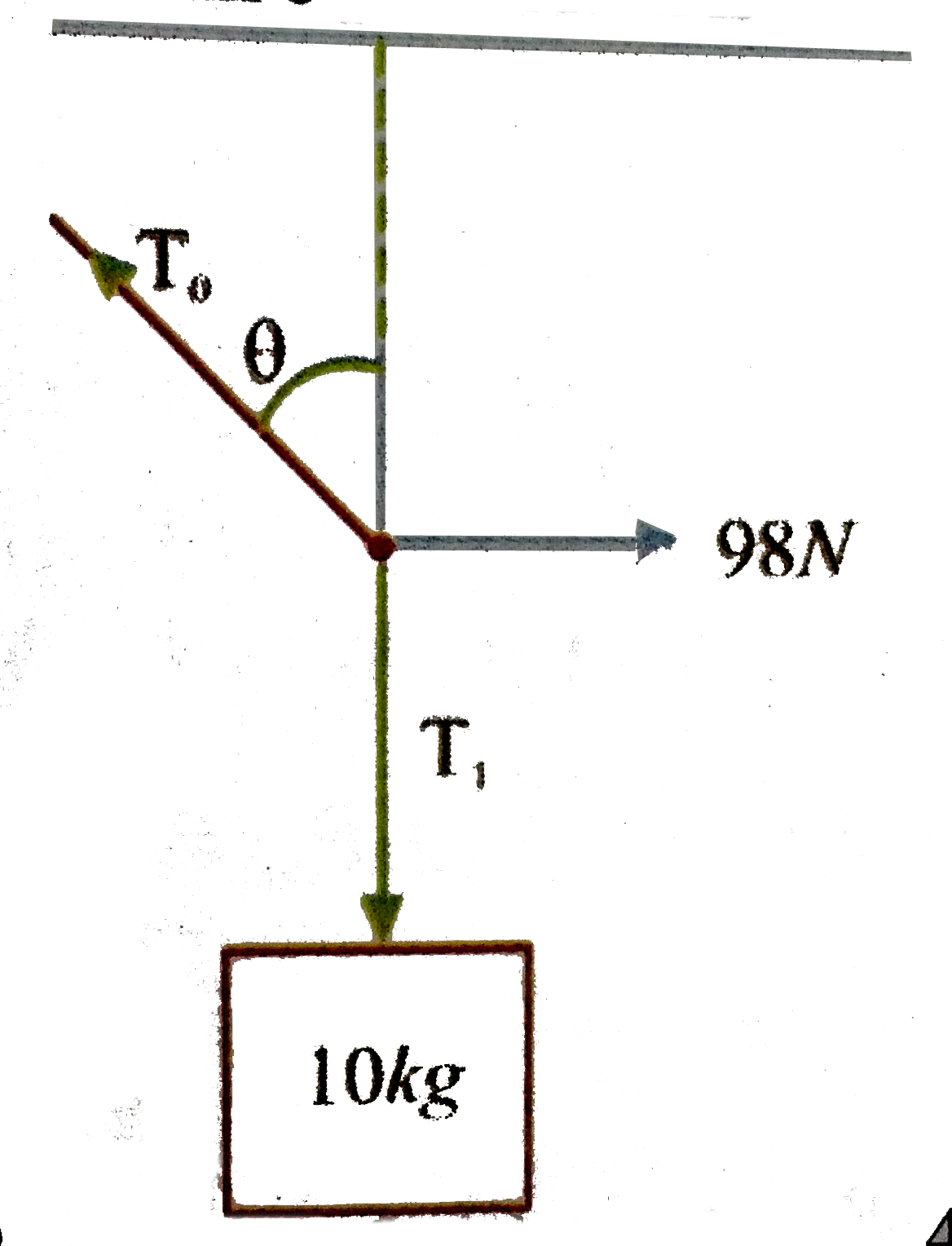 .A30∘B60∘C45∘D90∘
.A30∘B60∘C45∘D90∘
A mass of 20 kg is suspended by a rope of length 2 m from a ceiling. A force of 173.2 N in the horizontal direction is applied at the midpoint of the rope as shown in Fig. What is the angle the rope makes with the horizontal in equilibrium ? Take g = 10ms−2. Neglect mass of the rope.
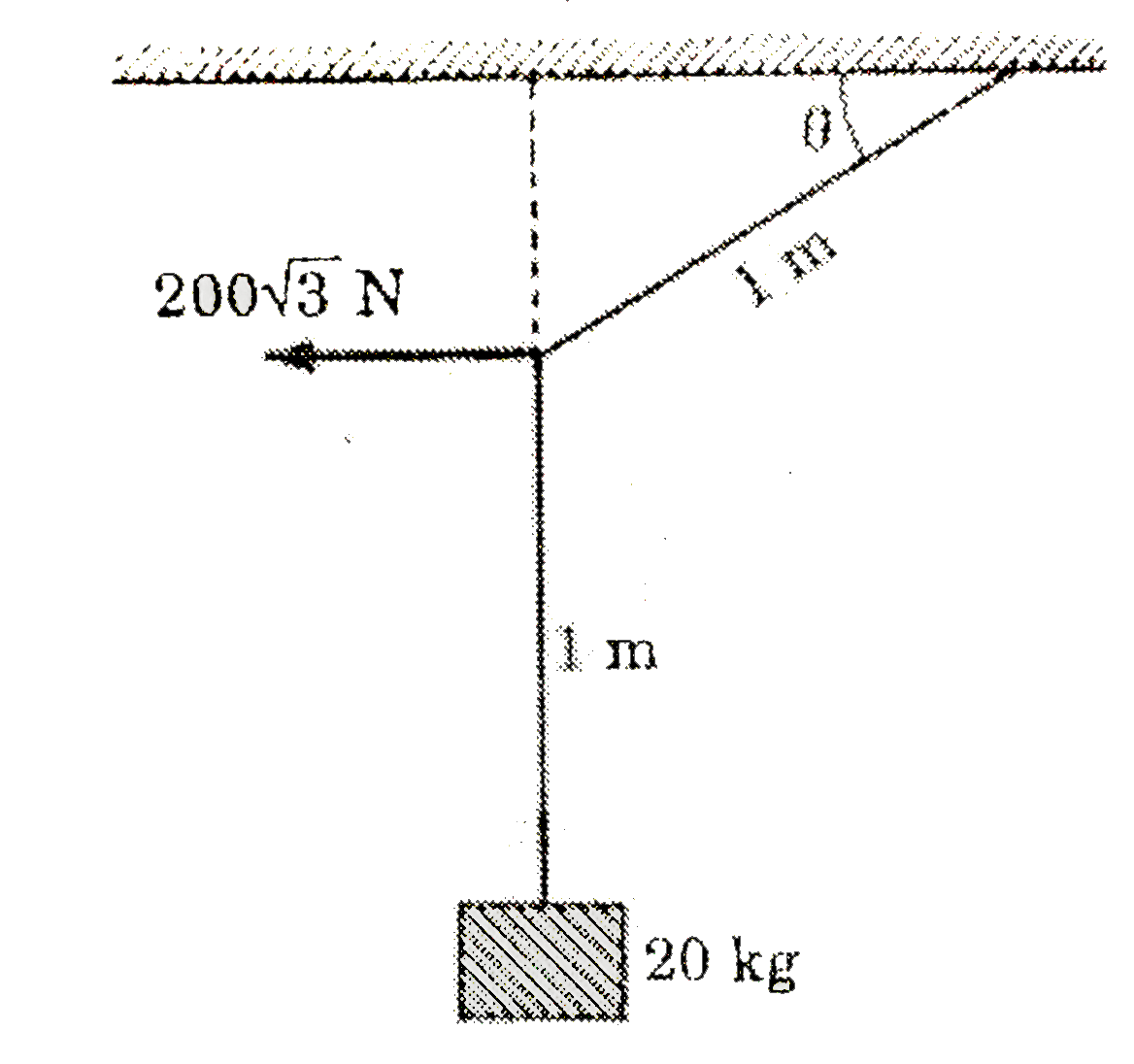
View SolutionA mass of 10 kg is suspended vertically by a rope from the roof. When a horizontal force is applied on the rope at some point, the rope deviated at an angle of 45∘ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (g=10ms−2)
View SolutionA mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
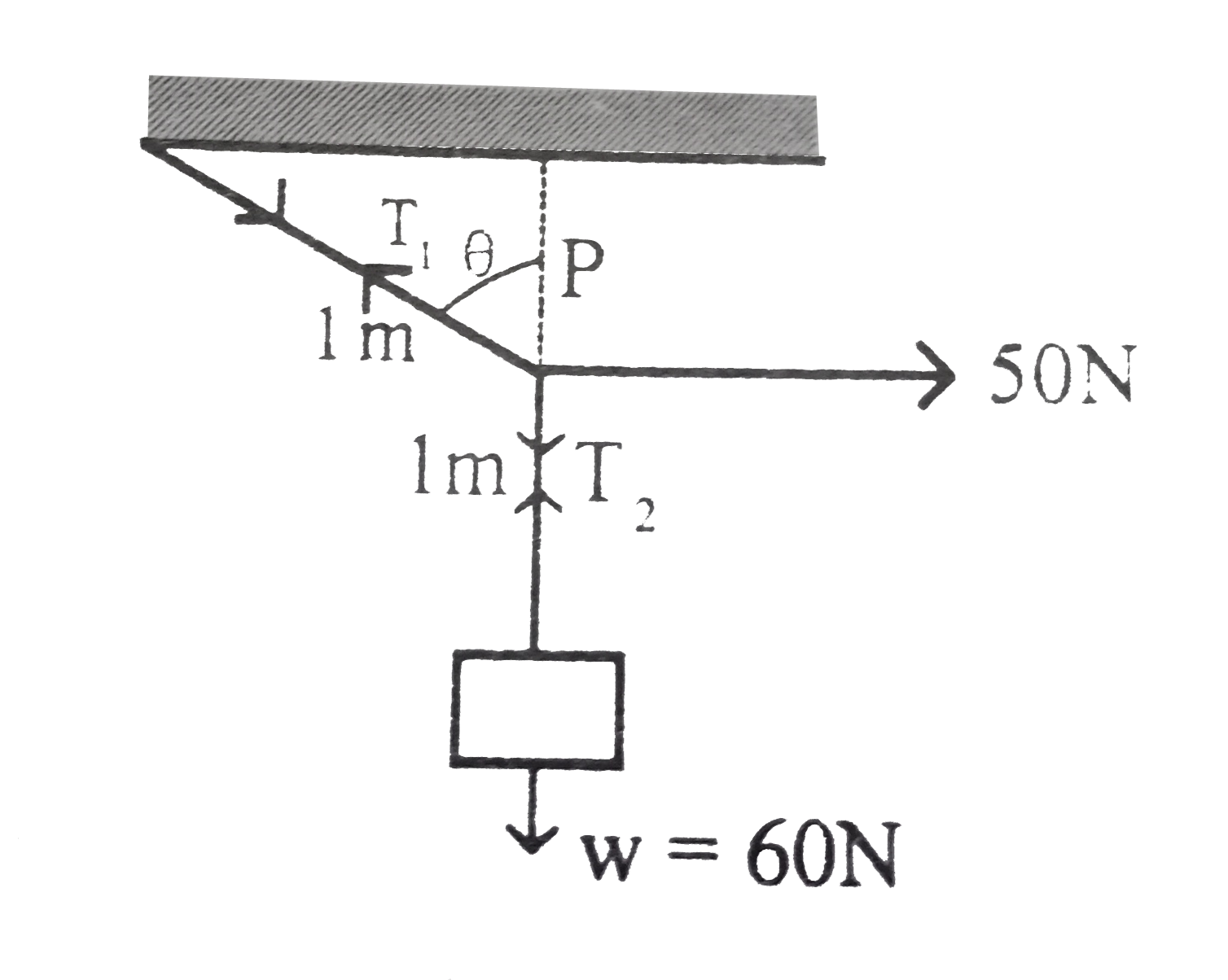
View SolutionA block of mass 5kg is suspended by a massless rope of length 2 m from the ceiling. A force of 50 N is applied in the horizontal direction at the midpoint P of the rope, as shown in the figure. The angle made by the rope with the vertical in equilibrium is (Take g=10ms−2m .
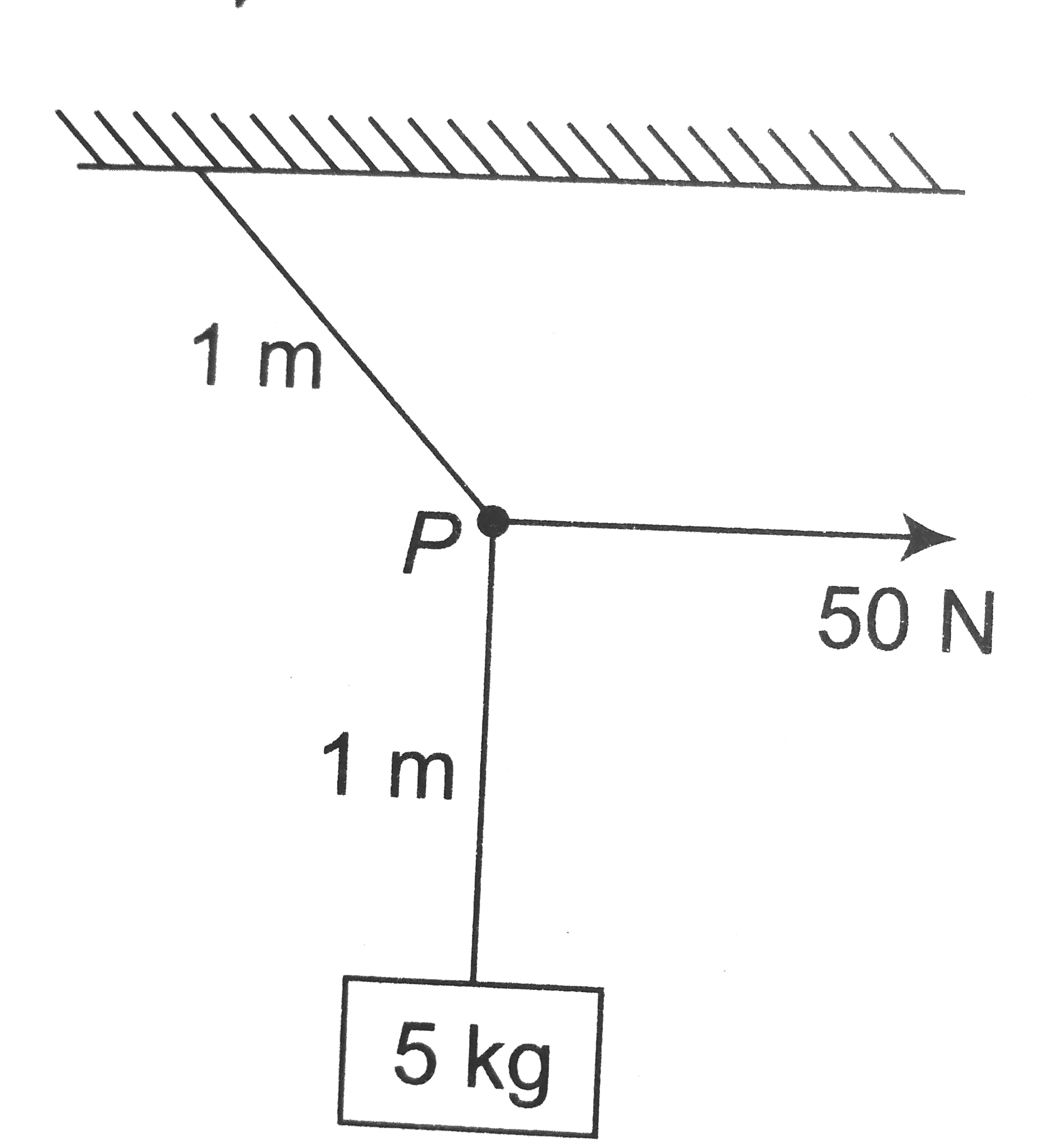
View SolutionA mass of 4kg is suspended by a rope of length 4m from a ceiling. A force of 20N in the horizontal direction is applied at the mid-point of the rope as shown in figure. What is the angle which the rope makes with the vertical in equilibrium? Neglect the mass of the rope. Take g=10ms−2 .
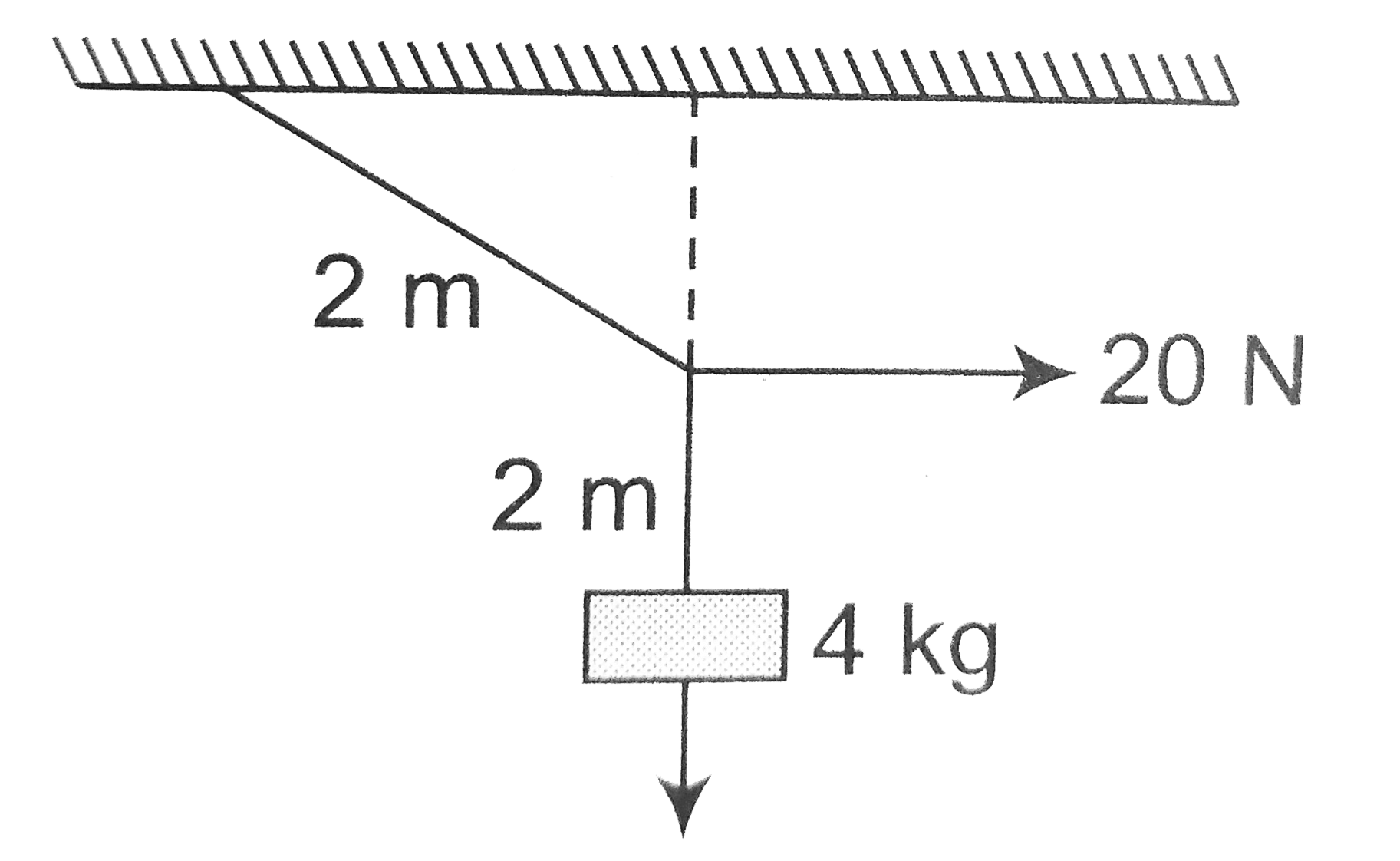
View Solution
