Water drops are falling from a nozzle of a shower onto the floor, from a height of 9.8 m. The drops fall at a regular interval of time. When the first drop strikes the floor, at that instant, the third drop begins to fall. Locate the position of second drop from the floor when the first drop strikes the floor.
m
m
m
m
To solve the problem, we need to determine the position of the second drop from the floor when the first drop strikes the floor. We will follow these steps:
Step 1: Calculate the time taken for the first drop to hit the ground.
The height from which the drops are falling is given as H=9.8m. We can use the second equation of motion to find the time taken for the first drop to reach the ground:
H=12gt2
Where:
- H=9.8m
- g=9.8m/s2 (acceleration due to gravity)
- t is the time taken to fall.
Substituting the values:
9.8=12×9.8×t2
This simplifies to:
9.8=4.9t2
Dividing both sides by 4.9:
t2=2⟹t=√2s
Step 2: Determine the time interval between the drops.
Since the drops fall at regular intervals, and when the first drop strikes the ground, the third drop begins to fall, we can infer that the second drop must have fallen for half the time it takes the first drop to reach the ground.
Thus, the time interval Δt between the drops is:
Δt=t2=√22s
Step 3: Calculate the position of the second drop when the first drop hits the ground.
The second drop has been falling for Δt seconds. We can use the second equation of motion again to find how far the second drop has fallen in this time:
h=12g(Δt)2
Substituting Δt=√22:
h=12×9.8×(√22)2
Calculating (√22)2=24=12:
h=12×9.8×12=9.84=2.45m
Step 4: Determine the position of the second drop from the floor.
The second drop has fallen 2.45m from the height of 9.8m:
Position from the floor=H−h=9.8−2.45=7.35m
Final Answer:
The position of the second drop from the floor when the first drop strikes the floor is 7.35m.
---
The height from which the drops are falling is given as H=9.8m. We can use the second equation of motion to find the time taken for the first drop to reach the ground:
- H=9.8m
- g=9.8m/s2 (acceleration due to gravity)
- t is the time taken to fall.
Since the drops fall at regular intervals, and when the first drop strikes the ground, the third drop begins to fall, we can infer that the second drop must have fallen for half the time it takes the first drop to reach the ground.
The second drop has been falling for Δt seconds. We can use the second equation of motion again to find how far the second drop has fallen in this time:
The second drop has fallen 2.45m from the height of 9.8m:
The position of the second drop from the floor when the first drop strikes the floor is 7.35m.
Topper's Solved these Questions
Similar Questions
Water drops from the nozzle of a shower into the stall floor 176.4 m below. The drops fall at regular interval of time, the first drop striking the floor at the instant the fourth drop begins to fall. Find the location of the individual drops when a drop strikes the floor. Take g=9.8m/s2
View SolutionWater drips from the nozzle of a shower onto the floor 200 cm below. The drops fall at regular ( equal) intervals of time, the first drop striking the floor at the instant the fourth drop begins to fall. When the first drop strikes the floor, how far below the nozzle are the (a) second and (b) third drops ?
View Solution
Knowledge Check
Drops of water fall from the roof of a building 9m. High at regular intervals of time, the first drop reaching the ground at the same instant fourth drop starts to fall. What are the distance of the second and third drops from the roof?
A6 m and 2 mB6 m and 3 mC4 m and 1 mD4 m and 2 mWater drops fall from a tap on to the floor 5.0 m below at regular intervals of time. The first drop strikes the floor when the fifth drops beings to fall. The height at which the third drop will be from ground at the instant when the first drop strikes the ground is (take=g=10m−2)
A1.25 mB2.15 mC2.75 mD3.75 mA body falling from a height of 10m rebounds from the hard floor . It
A0.89B0.56C0.23D0.18
water drops trickle out from a nozzle and fall on the height 4.0 m below at regular intervals. When first drop reaches the floor, the fifth drop begins to fall. Find the positive of the drops , when a drop just strikes the floor.
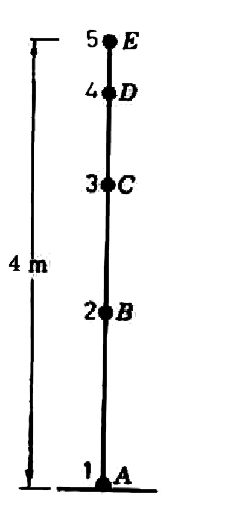
View SolutionDrops of water from the roof of a house 6 m high fall at regular intervals. The first drop reaches the ground at an instant of time when third drop leaves the roof. Find the height of the second drop at that instant
View SolutionWater drops are falling in regular intervals of time from top of a tower to height 9 m. If 4th drop begins to fall when 1st drop reaches the ground, find the positions of 2nd&3rd drops from the top of the tower.
View SolutionDrops of water fall at refular intervais from the roof of a building of height H = 5 m, the first drop strikes the ground at the same moment when the fifth drop detaches itself from the roof. Then ratio of distances first drop reaches the ground are :
View SolutionWater drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap, the instant the first drop touches the ground. How far above the ground is the second drop at that instant. (g=10ms−2)
View Solution
