A vertical cylinder of height 100cm contains air at a constant temperature. The top is closed by a friction less light piston. The atmospheric pressure is equal to 75 cm of mercury. Mercury is slowly poured over the piston. Find the maximum height of the mercury column that can be put on the piston.Solution in Tamil
Given, P1=A→mosphericpressure
=75×ρg,
V1=100×A
(P2)=Atmosphericpressure
+ Mercury pressure
=75ρg+hρg
(ifh=heightofmercury)
V2=(100−h)
((P1)(V1))=((P2)(V2))
⇒75ρg(100A)
=((75+h)ρg(100−h)A)
⇒(75×100)=((75+h)(100−h))
⇒7500=7500−75h+100h−(h2)
⇒(h2)−100h+75h=0
h2−25h=0
⇒(h2)=25h
h=25cm
Height of Mercury that can be poured
=25cm .
Topper's Solved these Questions
Similar Questions
Find the dimensions of
a. linear momentum
b. frequency and
c. pressure05:12View SolutionShould the internal energy of a system necessarily increase if heat is added to it?
03:16View SolutionA berometer correctlu reads the atmospheric pressure as 76cm of mercury. Water droplets are slowly introduced into the barometer tube by a dropper. The height of the mercury column first decreases and then become constant. If the saturation vapour pressure at the atmospheric tgemperature is 0.80cm of mercury, find the height if the mercury column when it reaches its minimum value.
View SolutionThe arms of a U shaped tube are vertical. The arm on right side is closed and other arm is closed by light movable piston. There is mercury in the tube and initially the level of the mercury in the arms is the same. Above the mercury, there is an air column of height h in each arm, and initial pressure is the same as atmospheric pressure in both arms. Now pistion is slowly pushed down by a distance of h/2 (see figure)
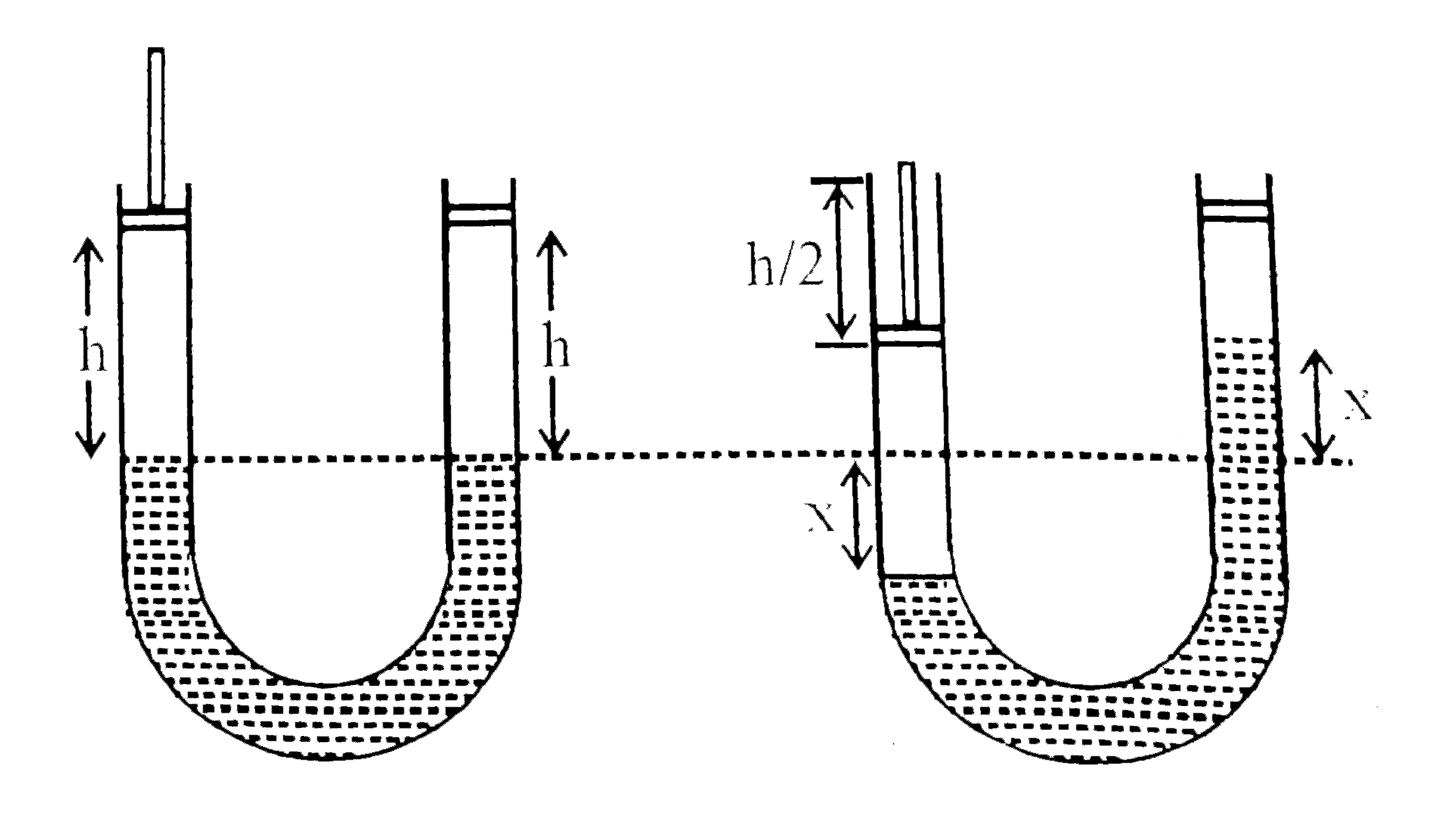
Let x is the displacement of mercury level in one of the stem and P1 is pressure in left column of air after compression, P2 is pressure in right column of air after compression and P0 is atmospheric pressure then03:39View SolutionThe height of a mercury barometer is 75 cm at sea level and 50 cm at the top of a hill. Ratio of density of mercury to that of air is 10. The height of the hill is
02:25View SolutionThe height of a mercury barometer is 75 cm at sea level and 50 cm at the top of a hill. Ration of density of mercury to that of air is 104. The height of the hill is
02:21View Solutionएक वायुमंडलीय दाब को पारे के स्तम्भ की ऊंचाई के सन्दर्भ में परिभाषित कीजिए ।
04:20View SolutionAt normal atmospheric pressure the height of the mercury column in barometer is
06:23View Solution76 सेमी पारे के स्तम्भ के दाब के बराबर जल के स्तम्भ की ऊँचाई ज्ञात कीजिए |
View SolutionA vertical cylinder of height 100 cm contains air at a constant temperature and its top is closed by a frictionless piston at atmospheric pressure (76 cm of Hg) asshown in figure-2.12. If mercury is slowly poured on the piston, due to its weight airis compressed. Find the maximum height of the mercury column which can be put on the piston.
05:01View SolutionBoth limbs of a 'U' tube are of equal length. One of the limbs is sealed and contains a column of 28 cm of air at atmospheric pressure. The air is separated from the atmosphere by mercury. What will be the height of air in the sealed limb, if the other limb is now filled to the top with mercury ? Atmospheric pressure is 76 cm of mercury.
05:02View SolutionA barometer correctly reads the atmospheric pressure as 76cm of mercury. Water droplets are slowly introduced into the barometer tube by a dropper. The height of the mercury column first decreases and then become constant. If the saturation vapour pressure at the atmospheric temperature is 0.80cm of mercury, find the height if the mercury column when it reaches its minimum value.
View SolutionA vertical hollow cylinder of height 1.52 m is fitted with a movable piston of negligible mass and thickness. The lower half portion of the cylinder contains an ideal gas and the upper half is filled with mercury. The cylinder is initially at 300 K. When the temperature is raised, half of the mercury comes out of the cylinder. Find this temperature, assuming the thermal ·expansion of mercury to be negligible.
View SolutionA vertical cylinder of height 100cm contains air at a constant temperature and its top is closed by a frictionless piston at atmospheric pressure (76 cm of Hg) as shown figure - a. If mercury is slowly poured on the piston, due to its weight air is compressed. Find the maximum height of the mercury column which can be put on the piston.
 View Solution
View SolutionA vertical cylinder of height 100cm contains air at a constant temperature and its top is closed by a frictionless pistion at atmospheric pressure (76cm of Hg) as shown figure (a). If mercury is slowly poured on the pistion, due to its weight air is compressed. Find the maximum height of the mercury column which can be put on the pistion.
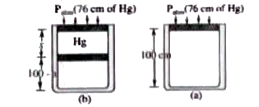 03:15View Solution
03:15View SolutionA vertical cylinder of height 100 cm contains air at a constant temperature and its top is closed by a frictionless pistion at atmospheric pressure (76 cm of Hg) as shown figure ( a). If mercury is slowly poured on the pistion, due to its weight air is compressed. Find the maximum height of the mercury column which can be put on the pistion.
 02:44View Solution
02:44View Solution

