Find the dimensions of
a. the specific heat capacity c,
b. the coeficient of linear expansion α and
c. the gas constant R
Some of the equations involving these quantities are
Q=mc(T2−T1),lt=l0[1+α(T2−T1)]andPV=nRT.Solution in Tamil
The correct Answer is:A, B, C
(a) Specific heat capacity
C=QmΔt=[ML2T−2][M][K]=[L2T−2K−1]
(b) Coefficient of linear expansion
α=L1−L0L0ΔT=[L][LK]=[K−1]
(c) Gas constant
R=PVnT=[ML−1T−2][L3](mol)[K])=[ML2T−2K−1(mol)−1])
Topper's Solved these Questions
Similar Questions
The dimensions ML−1T−2 may correspond to
06:48View SolutionA uniform slab of dimension 10cm×10cm×1cm is kept between two heat reservoir at temperatures 10∘C and 90∘C. The larger surface areas touch the reservoirs. The thermal conductivity of the material is 0.80Wm−1C−1 . Find the amount of heat flowing through the slab per minute.
09:04View SolutionCalculate the rms speed of nitrogen at STP (pressure =1 atm and temperature =00C. The density of nitrgoen in these conditions is 1.25kgm−3
02:56View Solutiont1=(sinθ)cosθ,t2=(sinθ)sinθ,t3=(cosθ)cosθ,t4=(cosθ)sinθ (A) t3>t1>t2 (B) t4>t2>t1 (C) t4>t1>t2 (D) t1>t3>t2
03:14View SolutionThe vertices of a triangle are [a t_1t_2,a(t_1 +t_2)], [a t_2t_3,a(t_2 +t_3)], [a t_3t_1,a(t_3 +t_1)] Then the orthocenter of the triangle is (a) (-a, a(t_1+t_2+t_3)-at_1t_2t_3) (b) (-a, a(t_1+t_2+t_3)+at_1t_2t_3) (c) (a, a(t_1+t_2+t_3)+at_1t_2t_3) (d) (a, a(t_1+t_2+t_3)-at_1t_2t_3)
08:14View SolutionFind the dimensions of
a. angular speed ω
angular acceleration α
torque τ and
d. moment of interia I.<br>.Someoftheequations∈volv∈gthesequantitiesareomega=(theta_2-theta_1)/(t_2-t_1), alpha = (omega_2-omega_1)/(t_2-t_1), tau= F.r and I=mr^2
The symbols have standard meanings.04:47View SolutionThe related equations are : Q=mc(T2−T1),l1=l0[1+α(T2−T1)] and PV−nRT,
where the symbols have their usual meanings. Find the dimension of
(A) specific heat capacity (C) (B) coefficient of linear expansion (α) and (C) the gas constant (R).06:32View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+at1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
02:06View SolutionIf the normals at points t1 and t2 meet on the parabola, then
(a) t1t2=1 (b) t2=−t1−2t1 (c) t1t2=2 (d) none of these03:09View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is: (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+a(t1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
03:28View SolutionFind the dimensions of
a. angular speed ω
angular acceleration α
torque τ and
d. moment of interia I.
. Some of the equations involving these quantities are ω=θ2−θ1t2−t1,α=ω2−ω1t2−t1,τ=F.randI=mr2
The symbols have standard meanings.02:51View SolutionA gas follows PV12=constant as shown. If V2=2V1 , find T2T1
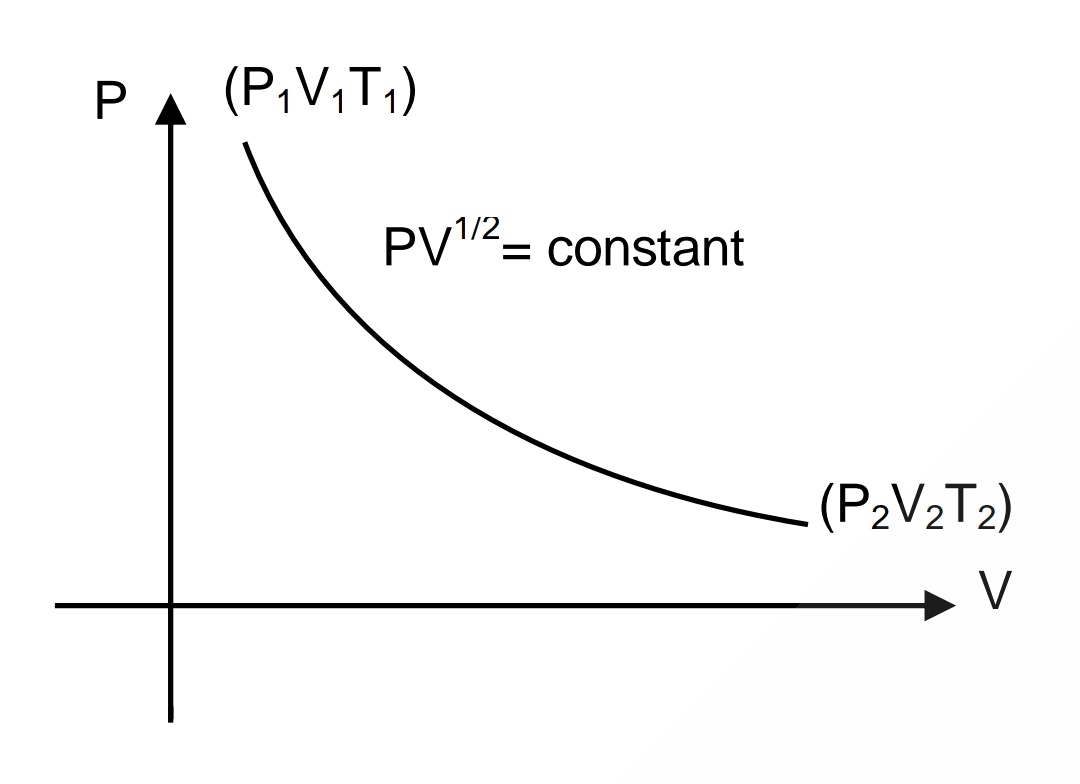 02:27View Solution
02:27View Solutionযদি (a+b)t1=(b+c)t2=(c+d)t3=(a+d)t হয় তবে প্রমাণ করো যে , 1t=1t1−1t2+1t3।
05:57View SolutionThe normal drawn at a point (at21,−2at1) of the parabola y2=4ax meets it again in the point (at22,2at2), then t2=t1+2t1 (b) t2=t1−2t1 t2=−t1+2t1 (d) t2=−t1−2t1
05:58View SolutionThe vertices of a triangle are [a t_1t_2,a(t_1 +t_2)] , [a t_2t_3,a(t_2 +t_3)] , [a t_3t_1,a(t_3 +t_1)] Then the orthocenter of the triangle is (a) (-a, a(t_1+t_2+t_3)-at_1t_2t_3) (b) (-a, a(t_1+t_2+t_3)+at_1t_2t_3) (c) (a, a(t_1+t_2+t_3)+at_1t_2t_3) (d) (a, a(t_1+t_2+t_3)-at_1t_2t_3)
04:16View SolutionThe related equations are : Q=mc(T2−T1),l1=l0[1+α(T2−T1)] and PV−nRT,
where the symbols have their usual meanings. Find the dimension of
(A) specific heat capacity (C) (B) coefficient of linear expansion (α) and (C) the gas constant (R).03:44View Solution

