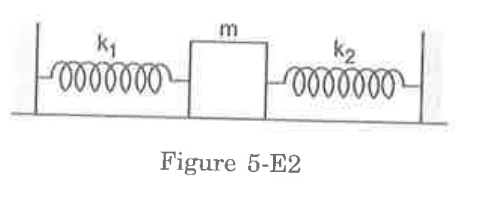
Both the springs shown in figure are untretched. If the block is displaced by a distance x and released, what will be the initial acceleration?
 Solution in Tamil
Solution in Tamil
Given, x=20cm=0.2m,
k=15Nm,m=0.3kg
Ae≤ration,a=Fm=−kxm=−15(0.2)0.3
= - 3/0.3 = - 10 m/s^2
(deceleration),
So, the acceleration is 10 m/s^2 opposite to the direction of motion.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -28videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer14videos
LAWS OF THERMODYNAMICS
- BOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises34videos
PHYSICS AND MATHEMATICS
Similar Questions
A refrence frame attached to the earth
04:11View SolutionShould the internal energy of a system necessarily increase if heat is added to it?
06:32View SolutionA vector →A makes an angle of 20∘and→B makes an angle of 110∘ with the X-axis. The magnitude of these vectors are 3 m and 4 m respectively.Find the resultant
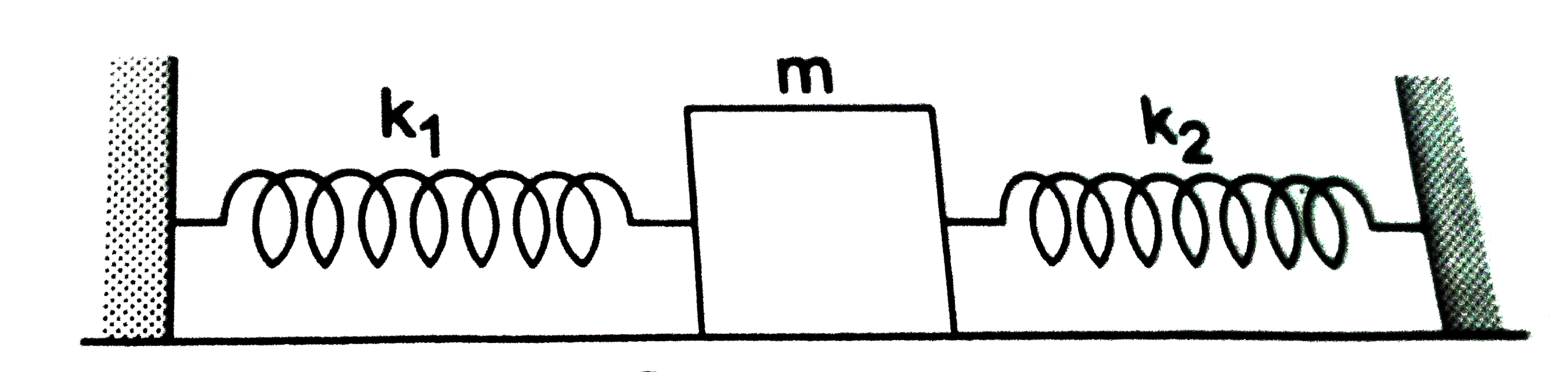
04:11View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 02:30View Solution
02:30View SolutionA block of mass m is attached to two unstretched springs of spring constant k , each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 07:13View Solution
07:13View SolutionA block of mass m is attached to the two springs in vertical plane as shown in the figure - 3.95. If initially both the springs are at their natural lengths then velocity of the block is maximum at displacement x given as
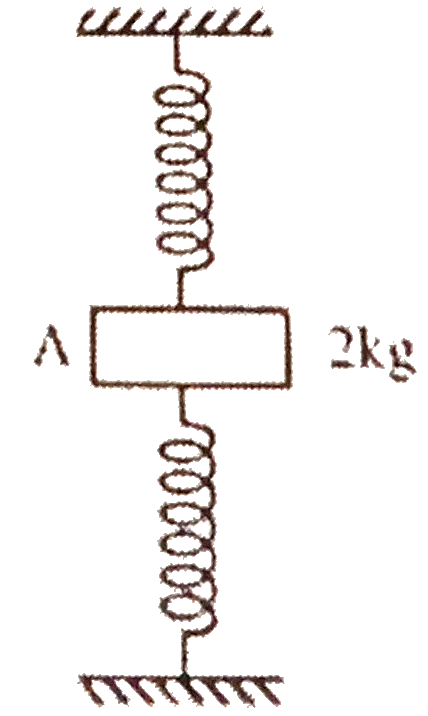
03:21View SolutionA block A of mass 2 kg is connected with two springs, as shown . The spring constant of lower spring is system is thrice the spring costant of upper spring. The system is released from rest with both the springs unstreched. The maximum displacement of bloack is 0.1m. Find the acceleration of the block is its lowest position-
 06:03View Solution
06:03View SolutionConsider the spring block system shown in the figure. Initially block m is in equilibrium. Then block m is displaced b y a small distance h. Find the maximum speed of the block. ltbgt
View Solutionचित्र में दिखाए गए दोनों स्प्रिंग अपनी स्वाभाविक लंबाई में हैं | यदि ब्लॉक को दाहिनी ओर x दूरी तक विस्थापित करके छोड़ दिया जाए, तो प्रारंभिक त्वरण कितना होगा ?
 View Solution
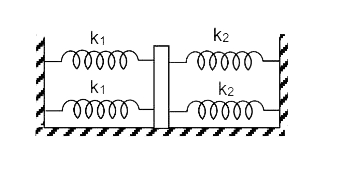
View SolutionA block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
 View Solution
View SolutionIn the system shown in figure, the block A is released from rest. Find
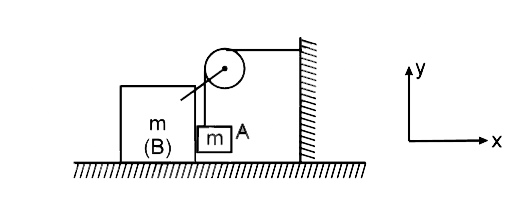
the acceleration of both blocks ‘A’ and ‘B’.02:03View SolutionA block of mass m is attached to two unstretched springs of spring constant k_(1) and k_(2) as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x//4 from its mean position. All the surfaces are smooth.
02:26View SolutionIn the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.
 03:26View Solution
03:26View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.
 03:28View Solution
03:28View SolutionA block of mass m is attached to two unstretched springs of springs constant k1 and k2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.
 03:14View Solution
03:14View Solution

