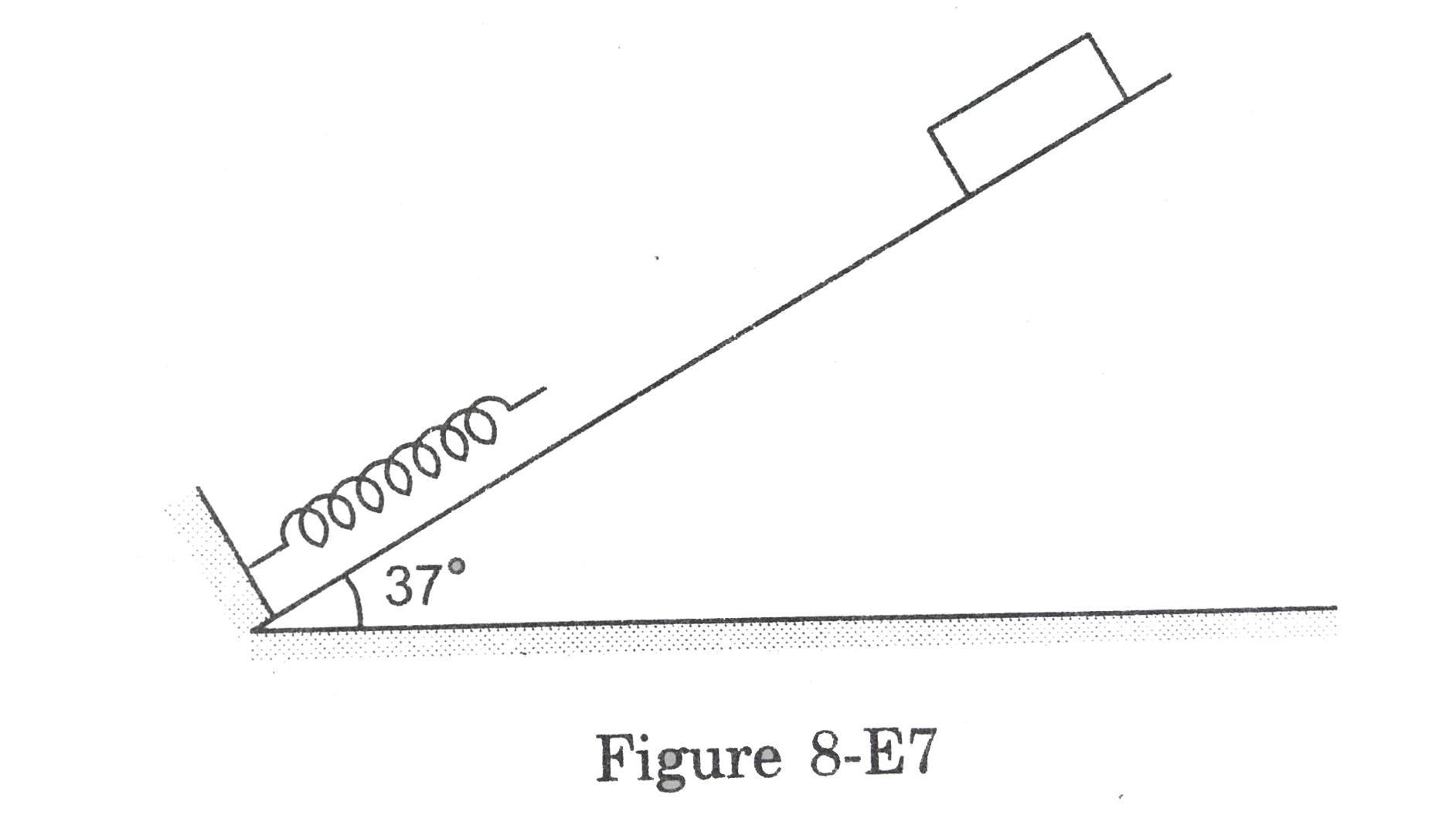
Figure shows a spring fixed at the bottom end of an incline of inclination 370. A small block of mass 2 kg starts slipping down the incline from a point 4.8 m away from the spring. The block compresses the spring by 20 cm, stops momentarily and then rebounds through a distance of 1 m up the incline. Find a. the frictioin coefficient between the plane and the block and b. the spring constant of the spring. Take g=10ms2.
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B
m=2kg,S1=4.8m,x=20cm=0.2m
S2=1m
sin370=0.60=35
θ=370
cos 37^0=0.80=4/5=10m/sec^2<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C08_E01_080_S01.pngwh=80%sty≤=background:white;><br>Apply∈gworke≠rgypr∈cip≤fordownwardmotionofthebody<br>0-0=mgsin37^0(x+4.8)-muRx5-1/2kx62<br>20xx(0.80)xx5-1/2k(0.2)^2=0<br>rarr 60-80mu-0.02k=0<br>→80mu+0.02k=60<br>Similarlyfortheupwardmotionofthebodytheequationis<br>0-0=(-mgsin37^0)-muRx1+1/(2k)(-2)^2<br>rarr 20xx(0.06)xx1-muxx20xx(0.80)xx1-1/2k(0.2)^2<br>rarr 12-16mu+0.02k=0<br>Adding equation i and equation ii we get
96μ=48
→μ=0.5
Now putting the value of μ in equation i,
k=1000Nm
Topper's Solved these Questions
Similar Questions
A heavy stone is thrown from a cliff of height h with a speed v. The stone will hit the ground with maximum speed if it is thrown
View SolutionA wave pulse passing on a string with speed of 40cms−1 in the negative x direction has its maximum at x=0 at t=0. Where will this maximum be located at t=5s?
View Solutiona. A 2-kg situated on a smooth fixed incline is connected to a spring of negligible mass, with spring constant k=100Nm^-1 , via a frictionless pulley. The block is released from rest when the spring is unstretched. How far does the block moves down the incline before coming (momentarily) to rest? What is its acceleration at its lower point? b. The experiment is repeated on a rough incline. If the block is observed to move 0.20m down along the incline before it comes to instantaneous rest, calculate the coefficient of kinetic friction.
View Solution
A 5-kg block rests on a smooth inclined plane of inclination 37∘ as shown in the diagram if the extension of spring is 6cm, find (a) the spring constant (b). If the block is pulled dow the incline 4 cm from its equilibrium position and released, find the initial acceleration of the block.
View Solutionblock of mass m slips down an inclined plane as shown in the figure. When it reaches the bottom it presses the spring by a length (spring length ltlth and spring constant = K) - (A) (2mgh/K)1/2

View SolutionA block of mass 'M' is slipping down on a rough inclined of inclination α with horizontal with a constant velocity. The magnitude and direction of total reaction from the inclined plane on the block is :
View SolutionA 1 kg block sIides down an inclined plane of mass 3.2kg having inclination 45^(@) . If the inclined plane is fixed and the 1kg block slides without friction, find the acceleration of the centre of mass of the system of the block and inclined plane.
View SolutionFigure. shows a rough incline at an angle theta with coefficient of friction mu At the bottom a spring is attached with force constant k. A block of mass m is released from a position at a length l away from the spring. Write down the work energy equations to find the maximum compression in the spring and the distance by which the block rebound up the inclined plane. the distance by which the block rebound up the inclined plane
View Solution37∘ पर झुके हुए एक आनत तल के निचले किनारे पर एक स्प्रिंग फिक्स किया गया हैं । स्प्रिंग से 4.8 m दूरी से 2kg द्रव्यमान का एक छोटा गुटका आनत तल पर फिसलना प्रारंभ करता हैं । गुटका स्प्रिंग को 20 cm संपीडित करके क्षणभर के लिए रुकता हैं तथा पुनः स्प्रिंग व्दारा पीछे की ओर धकेल दिया जाता हैं । यह आनत तल पर ऊपर की ओर 1m तकक दूरी तय करता हैं । स्प्रिंग का स्प्रिंग नियतांक निकालें (g = 10 m/s2)

View SolutionIn the figure show below, calculate the coefficient of friction between the block and the inclined plane. Assume that the mass of the block s 1 kg. The block is released from rest and stops by covering the distance of 0.1 m on the plane.
View SolutionIn figure a spring with k = 168 N//m is in its relaxed length and is at the top of a frictionless incline of angle theta = 37^(@) . The lower end of the incline is at distance D = 1 m from the end of the spring. A small blcok of mass 2 kg is pushed against the spring until the spring is compressed by 0.2 m and released from rest. What is the speed of the block at the instant the spring returns to its relaxed length (which is when the block loses contact with the spring)?
View SolutionIn figure a spring with k = 168 N//m is in its relaxed length and is at the top of a frictionless incline of angle theta = 37^(@) . The lower end of the incline is at distance D = 1 m from the end of the spring. A small blcok of mass 2 kg is pushed against the spring until the spring is compressed by 0.2 m and released from rest. What is the speed of the block when it reaches the lower end of the incline?
View SolutionA block of mass m slips down an inclined plane as shown in the figure. When it reaches the bottom it presses the spring by a length (spring length ⟨h and spring constant = K)-
View SolutionA spring with constant k = 78 N/m is at the base of a frictionless, 30.0^(@) inclined plane. A 0.50 kg block is pressed against the spring, compressing it 0.20 m from its equilibrium position. The block is then released. If the block is not attached to the spring, how far up the incline will it travel before it stops ?
View Solutiona. A 2−kg situated on a smooth fixed incline is connected to a spring of negligible mass, with spring constant k=100Nm−1, via a frictionless pulley. The block is released from rest when the spring is unstretched. How far does the block moves down the incline before coming (momentarily) to rest? What is its acceleration at its lower point?
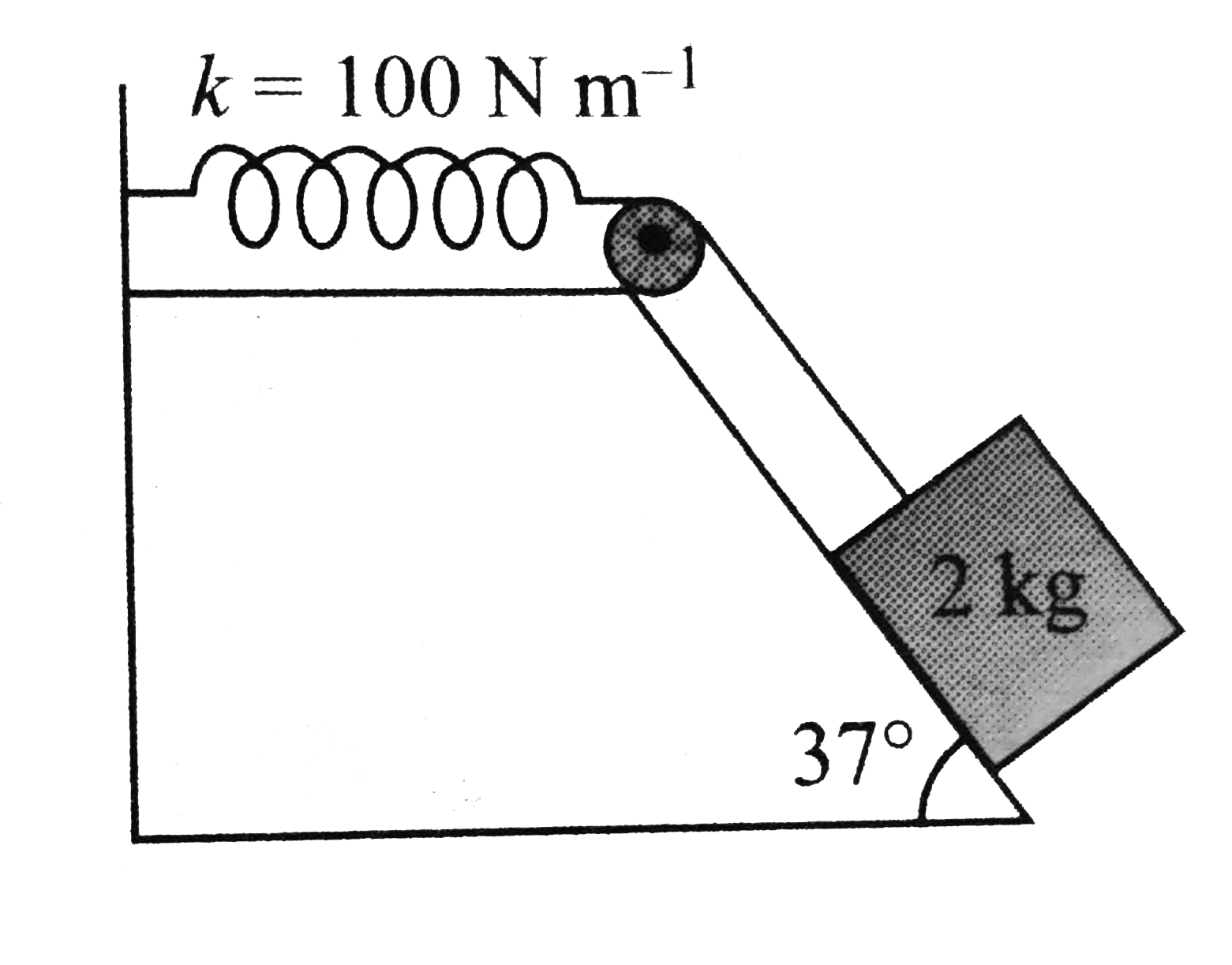
b. The experiment is repeated on a rough incline. If the block is observed to move 0.20m down along the incline before it comes to instantaneous rest, calculate the coefficient of kinetic friction.
View SolutionA block of mass 4 kg is released from the top of an inclined smooth surface as shown in figure If spring constant of spring is 100N/m and block comes to rest after compressing spring by 1 m, find the distance travelled by the block before it comes t o rest.

View Solution
