A heavy ring fo mass m is clamped on the periphery of a light circular disc.A small particle having equal mass is clamped at the centre of the disc. The system is rotated in such a way that the centre of mass moves in a circle of radius r with a uniform speed v. We conclude that an external force :Solution in Tamil
mv2r must be acting on the central particle
2mv2r must be acting on the central particle
2mv2r must be acting on the system
2mv2r must be acting on the ring
The correct Answer is:C
Step by step video & image solution for A heavy ring fo mass m is clamped on the periphery of a light circular disc.A small particle having equal mass is clamped at the centre of the disc. The system is rotated in such a way that the centre of mass moves in a circle of radius r with a uniform speed v. We conclude that an external force : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -211videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises64videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer25videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises18videos
CALORIMETRY
- BOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises30videos
CIRCULAR MOTION
Similar Questions
The centre of mass of a system of particles is at the origin. It follows that:
View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
03:31View SolutionCan the centre of mass of a body be at a point outside the body?
05:33View SolutionAn aluminium vessel of mass 0.5kg contains 0.2kg of water at 20∘C A block of iron of mass 0.2kgat100∘C is gently put into the water .Find the equilibrium temperature of the mixture, Specific heat capacities of aluminium , iron and water are 910Jkg−1K−1470Jkg−1K−1and4200Jkg−1K−1 respectively
04:41View SolutionFind the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
02:52View SolutionIf there are no external forces, the centre of mass of a double star moves like a free particle. If we go to the centre of mass frame, then we find that the two starts are moving in a circle about the centre of mass, which is at rest.
04:49View SolutionFrom a uniform circular dis of radius R , a circular dis of radius R//6 and having centre at a distance R//2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
03:16View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
05:30View SolutionA particle of mass m is placed at a distance R from centre of a uniformly dense thin ring of mass m rand radius R on a axis passing through its centre and perpendicular to its plane. Find the speed of the particle when it reaches at the centre fo the ring due to their mutual gravitation force.
38:54View SolutionA disc of mass M = 2m and radius R is pivoted at its centre. The disc is free to rotate in the vertical plane about its horizontal axis through its centre O. A particle of mass m is stuck on the periphery of the disc. Find the frequency of small oscillations of the system about its equilibrium position.
02:55View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R/2. Find the centre of mass of the remaining part of the disc.
 View Solution
View SolutionFind the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
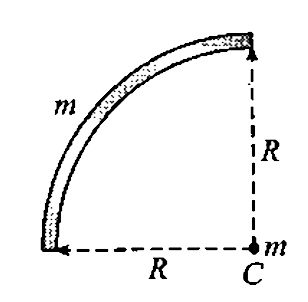 View Solution
View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
05:12View SolutionCbse | Centre Of Mass Of Rod | Centre Of Mass Of Semi Circular Ring | Centre Of Mass Of Half Disc
03:59View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
03:48View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
05:15View Solution

