A projectile is fired with a speed u at an angle θ above a horizontal field. The coefficient of restitution of collision between the projectile and the field is e. How far from the starting point does the projectile makes its second collision with the field?Solution in Tamil
The correct Answer is:A, B
The projected velocity =u
The angle of prjection =θ
Whentehprojectilehits the ground for the 1st time,
The velocity would be the same i.e u
Here the component of velocity paralel to ground
ucosθ should remain constant
But teh verticla component of the projectile under goes.
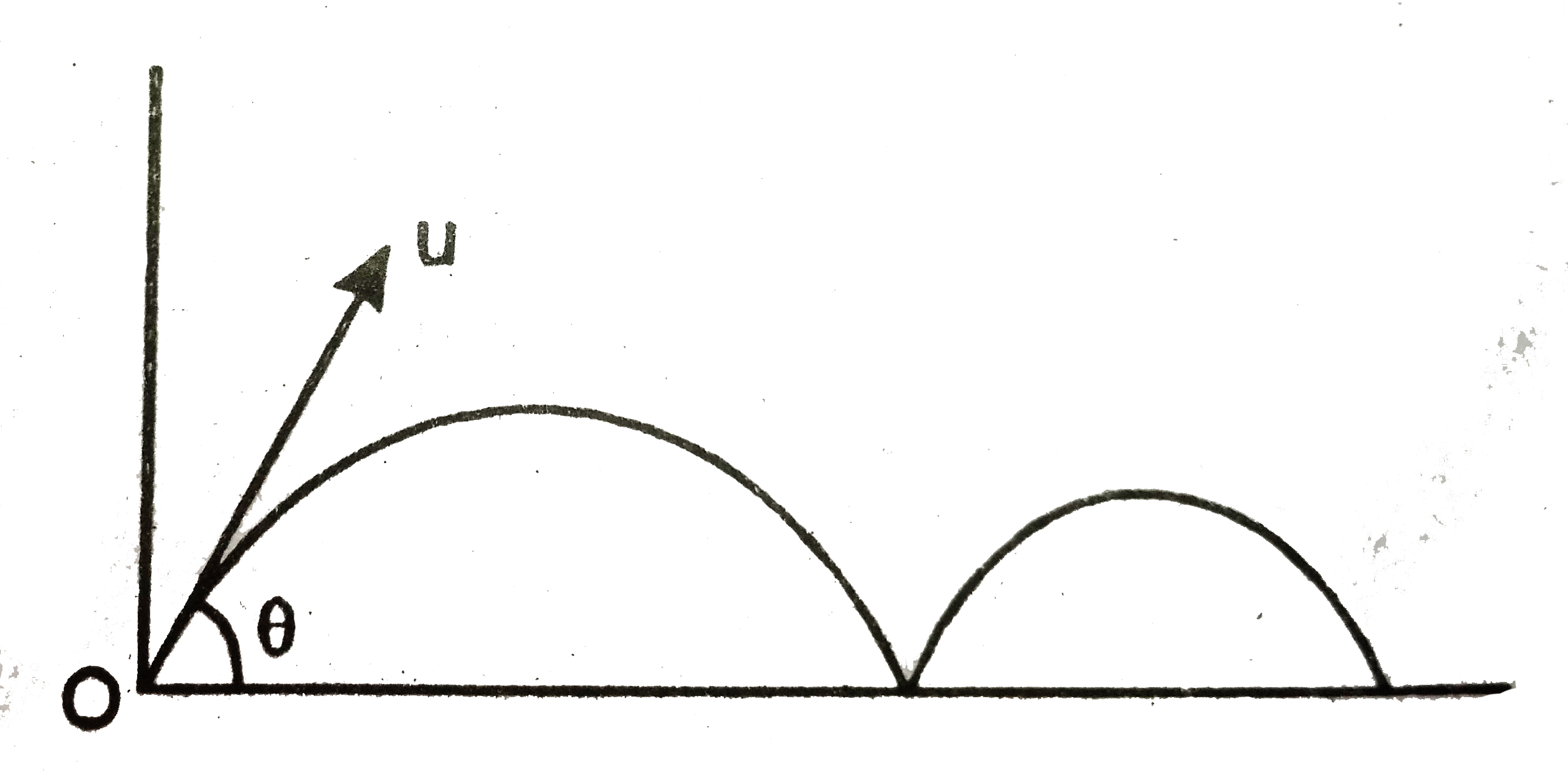
→v=eusinθ
Now for the 2nd projectile motion.
u=velocityofprojection<br>=sqrt((ucostheta)^2+(eusintheta)^2)<br>andAng≤ofprojection<br>=alpha=tan^I-1((eusintheta)/(ucostheta))<br>=tan^-1 (etantheta)<br>or taN/Alpha=etantheta..............2<br>Becausey=xtaN/Alphatan^-1(gx^2sec^2alpha)/(2u^2)............e<br>Here y=0, taN/Alpha<br>=etantheta<br>sec^2alha=1+e^2tan^2theta<br>andu^2=u^2cos^2theta+e^2u^2sin^2theta<br>pu∈gtheabovevalues∈theequation3<br>xetantheta=(gxx^2(1+e^2tan^2theta))/(2u^2(cos^2theta+e^2sintheta))<br>orx=2eu2tanθ(cos2θ+e2sin2θ)g(1+e2tan2θ)
=2eu2tanθ.cos2θg
eu2sin2θg
→So,omthe⋆t∈gp∮Oitwillfasllatadistance<br>(u^2sin2theta)/g+(eu^2.sin2theta)/g<br>(u^2sin2theta)/g(1+e)
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
The centre of mass of a system of particles is at the origin. It follows that:
View SolutionAn aluminium vessel of mass 0.5kg contains 0.2kg of water at 20∘C A block of iron of mass 0.2kgat100∘C is gently put into the water .Find the equilibrium temperature of the mixture, Specific heat capacities of aluminium , iron and water are 910Jkg−1K−1470Jkg−1K−1and4200Jkg−1K−1 respectively
View SolutionFind the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
View SolutionA projectile is fired with a speed u at an angle θ with the horizontal. Find its speed when its direcrtion of motion makes an angle α with the horizontal.
View SolutionA projectile is projected from horizontal with velocity (u) making an angle 45∘ with the horizontal direction. Find the distance of the highest point of the projectile from its starting point.
View SolutionA projectile is projected with a speed u at an angle theta with the horizontal. What is the speed when its direction of motion makes an angle theta//2 with the horizontal
View SolutionA projectile is fired with a speed u at an angle theta above the horizontal field. The coefficient of restitution between the projectile and field is e. Find the position from the starting point when the projectile will land at its second collision
View SolutionA particle collides with a smooth, surface with speed u at an angle θ. Coefficient of restitution is e. Find the ratio of the horizontal ranges of two consecutive projectile motions
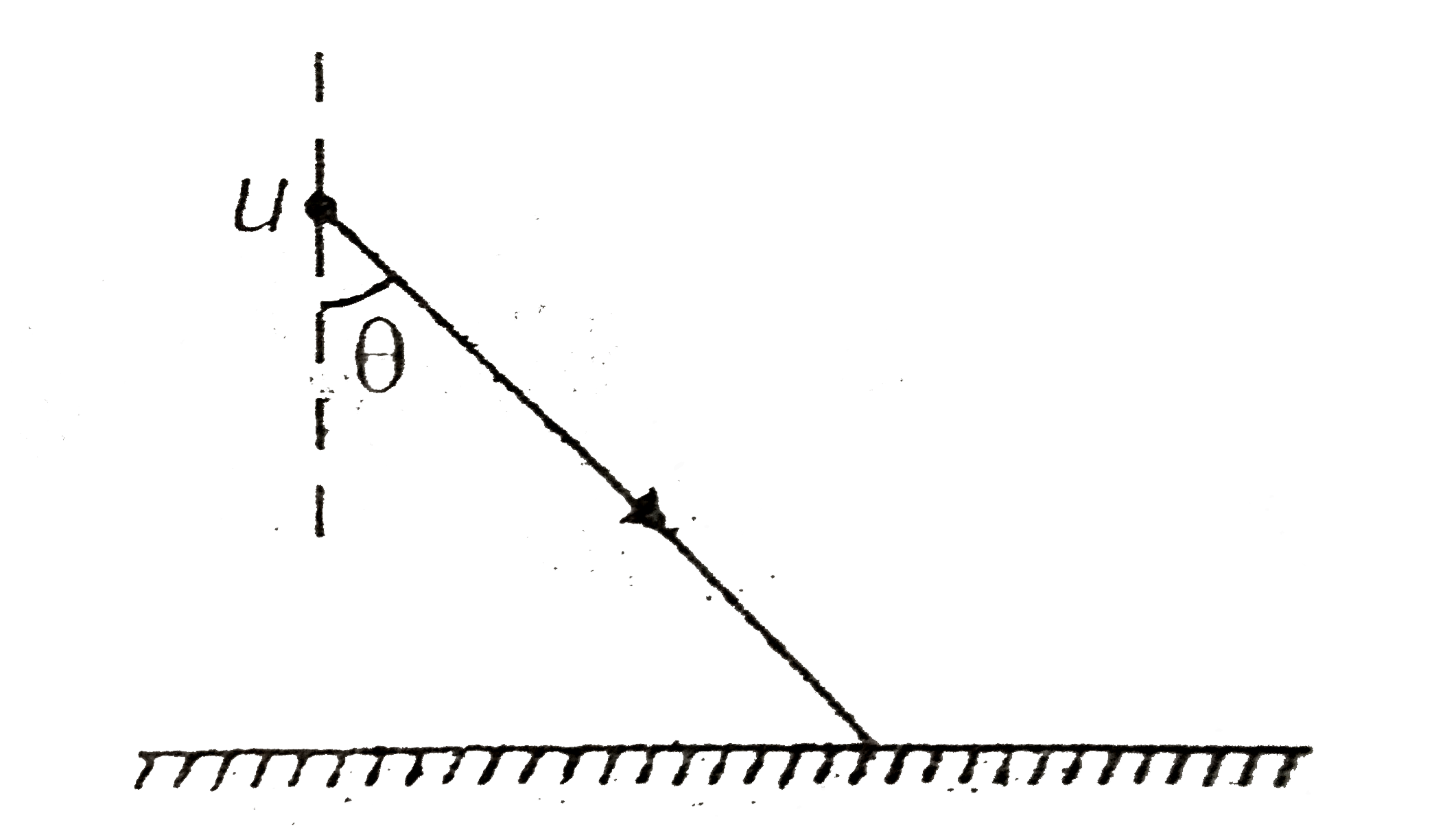
View Solutionएक मैदान में क्षैतिज दिशा से θ कोण बनाते हुए u चाल से एक प्रक्षेप्य प्रक्षेपित किया गया है। मैदान तथा प्रक्षेप्य के बीच प्रत्यवस्थान गुणांक e है। प्रारंभिक बिंदु से कितनी दूर प्रक्षेप्य मैदान के साथ दूसरी बार टकराएगा?
View SolutionA projectile is fired with velocity u making an angle θ with the horizontal. What is the angular momentum of the projectile at the highest point about the starting point ? (Given the mass of the projectile is m )
View SolutionA projectile is fired at an angle of 45∘ with the horizontal. Elevation angle of the projectile at its highest point as seen from the point of projection is
View SolutionFrom the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20" m s"^(-1) The horizontal range of the projectile is
View SolutionA projectile is projected with speed u at an angle theta with the horizontal . The average velocity of the projectile between the instants it crosses the same level is
View Solutionएक प्रक्षेप्य u वेग से क्षैतिज से 2θ कोण पर प्रक्षेपित किया जाता है। यदि इस प्रक्षेप्य का क्षैतिज से कोण θ हो जाये तो उस समय इसकी चाल होगी|
View SolutionA projectile is fired with a speed u at an angle theta with the horizontal. Find its speed when its direcrtion of motion makes an angle alpha with the horizontal.
View SolutionA projectile is fired with a velocity 'u' making an angle theta with the horizontal. Show that its trajectory is a parabola.
View Solution
