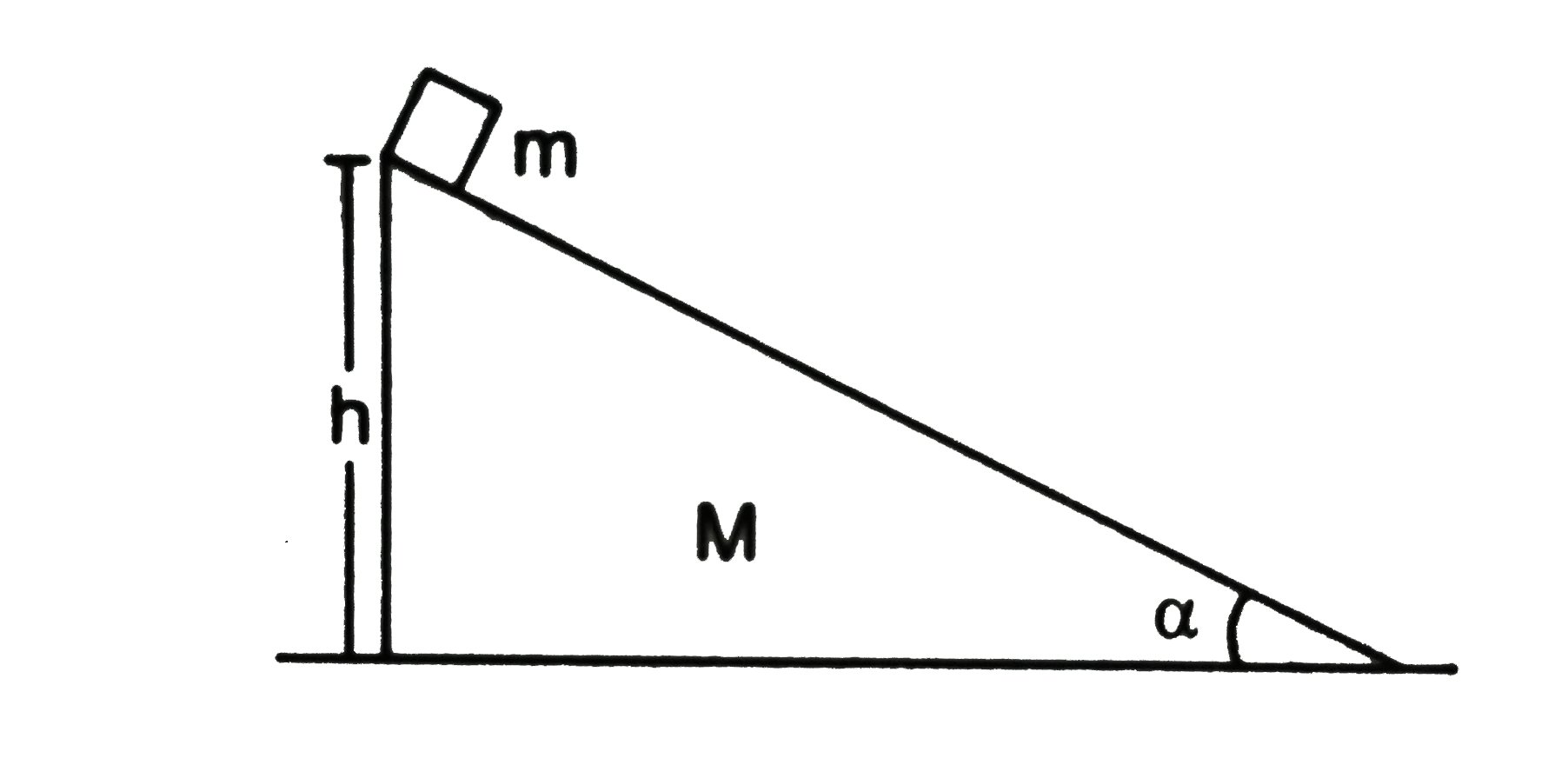
A block of mas m is placed on a triangular block of mas m, which in tunis placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B, C
The block m will slide down the inclined pklane of mass M with aceleration a1=gsinα (relative) to the inclined plane.
The horizontal component of a1 will be ax=gsinαcosα,forwhichtheblcokMwillae≤rate→wards≤ft,≤ttehae≤rationbea_2.<br>Aord∈g→theconceptofcentreofmass,(∈thehorizontldirecrtionexterNAlforceiszero)<br>ma_x=(M+m)a_2<br>rarr a_2=(ma_x)/(M+m)<br>=(mgsiN/Alpha cosalpha)/(M+m)......i<br>>sothe|o|lute(ress–tant)ae≤rationofmontheblockMalongthedirectionofthe∈cl∈ewillbe<br>a=gsiN/Alpha-a_2cosalpha<br>=gsiN/Alpha- (mgsiN/Alphacos^2alpha)/(M+m)<br>=gsiN/Alpha[1-(mcos^2alpha)/(M+m)]<br>=g sin alpha[(M+m-mcos^2alpha)/(M+m)]<br>So,a=g siN/Alpha [(M+msin^2alpha)/(M+m)]...ii<br>Letthetimetakenbytheblockm→reachthe⊥→mendbet<br>Now, S=ut+(1/2)at^2<br>rarrh/(siN/Alpha)=(1/2)at^2<br>rarr t=(sqrt(2h)/(a siN/Alpha))<br>So,thevelocityofthebig≥rblockaftertimetwillbe<br>v_m=u=a_2t<br>=(mgsiN/Alphacosalpha)/(M+m)<br>⎛⎝√2hαsiNAlpha⎞⎠
=⎡⎣2m2g2hsin2αcos2α(M+m)2asiNAlpha⎤⎦12
now substituting the value of a from equtioin ii we get
Vm=⎡⎣2m2g2hsin2α(M+m)2siNAlpha×cos2αgsiNAlpha(M+m)(M+msin2α)⎤⎦
or Vm=⎡⎢⎣2m2ghcos2α((M+m)(M+msin2α)]12
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
The centre of mass of a system of particles is at the origin. It follows that:
View SolutionAn aluminium vessel of mass 0.5kg contains 0.2kg of water at 20∘C A block of iron of mass 0.2kgat100∘C is gently put into the water .Find the equilibrium temperature of the mixture, Specific heat capacities of aluminium , iron and water are 910Jkg−1K−1470Jkg−1K−1and4200Jkg−1K−1 respectively
View SolutionFind the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
View SolutionFigure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mas m placed on a horizontal floor. The curved part of the surface shown is semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.

View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.
View SolutionA block of mass m is placed on a triangular block of mass M(M = 2m) , as shown. All surfaces are smooth. Calculate the velocity of triangular block when the smaller block reaches at bottom.
View SolutionAssuming all the surfaces to be smooth, find the acceleration of the triangular block of mass M when the block of mass m slides on it.

View Solution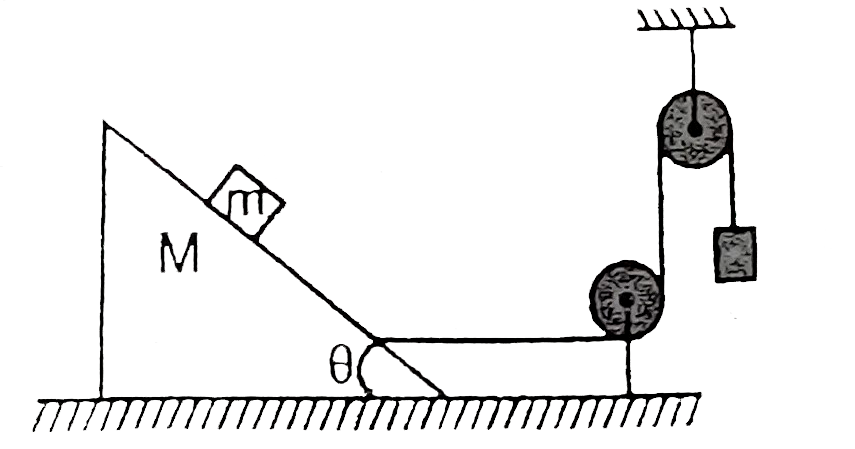
Find the mass (in kg) of the hanging block which will prevent the smaller block from slipping over the triangular block. All the surfaces are frictionless and the strings and the pulleys are light. Given m=M=1kg,cotθ=2,
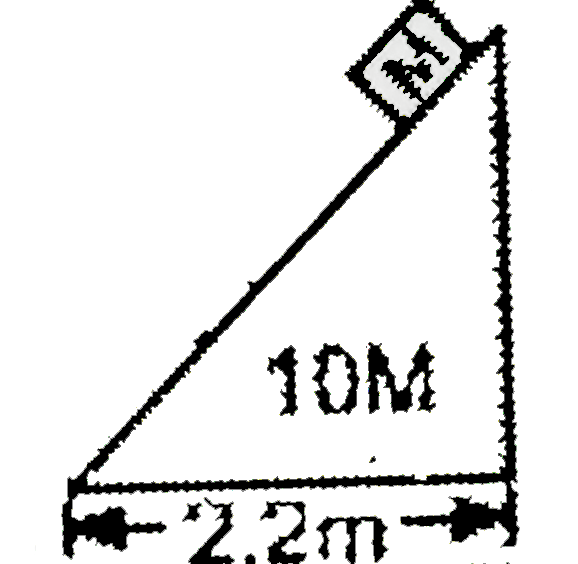
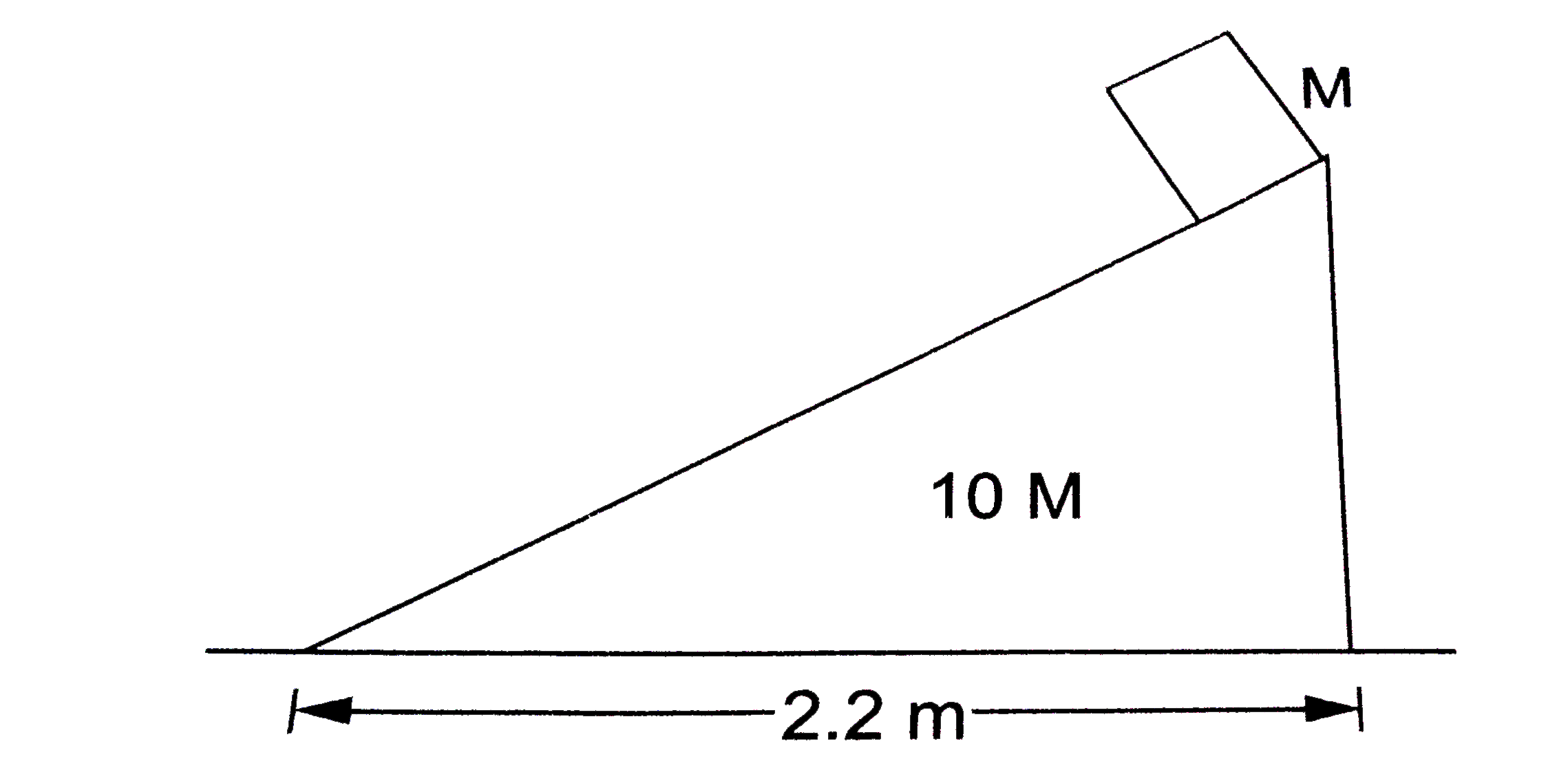
View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
View SolutionFind the mass of the hanging block in which will prevent the smaller block of mass m from slipping over the triangular block of mass M. All the surfaces are frictionless and the strings and the pulleys are light

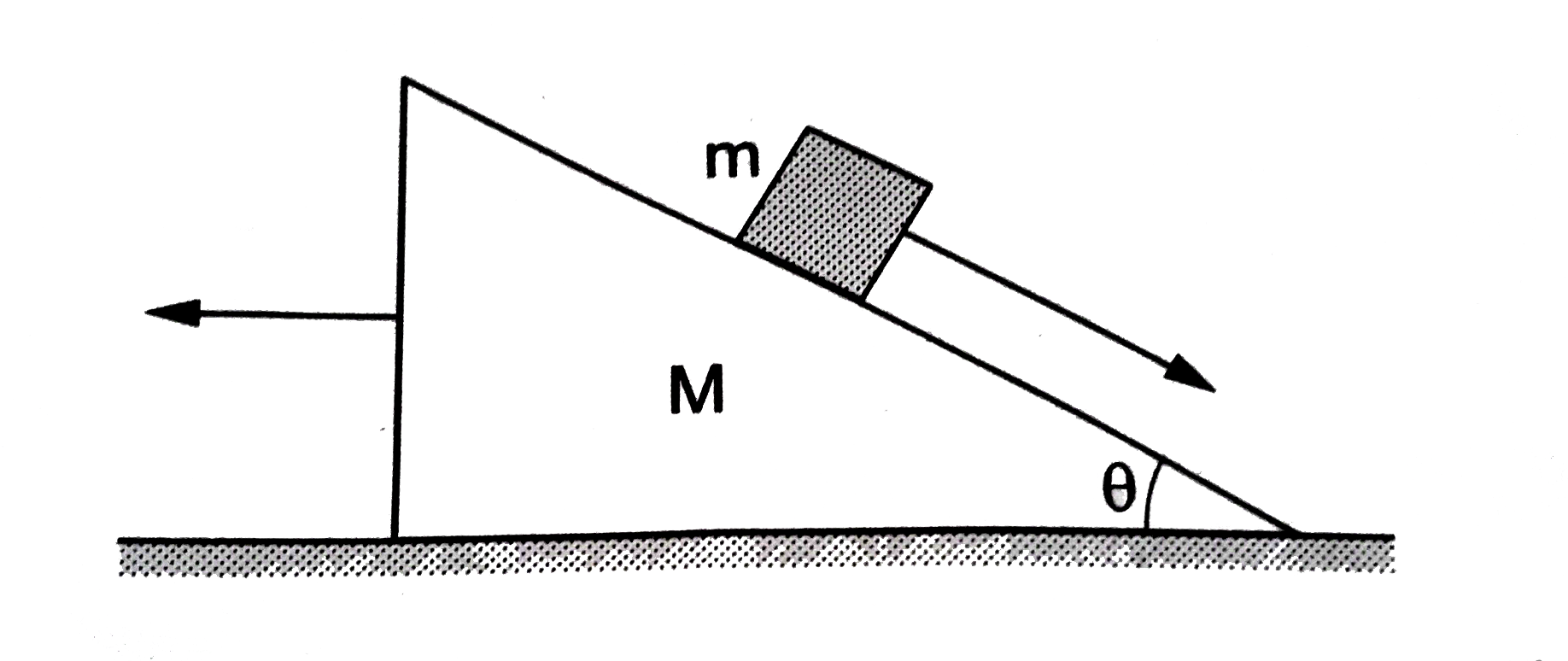
View Solutionचित्र 11.W2 में एक घर्षणरहित क्षैतिज सतह पर त्रिभुजाकार ब्लॉक रखा हुआ है जिसका द्रव्यमान M है। इसकी तिरछी सतह भी घर्षणरहित है और इस सतह पर m द्रव्यमान का एक छोटा गुटका रखा हुआ है। इस पूरी संहित को विराम की अवस्था में छोड़ दिया जाता है। ब्लॉक के सापेक्ष गुटके का त्वरण ज्ञात करे।
View Solutionचित्र में दिखाए अनुसार, एक स्थिर क्षैतिज सतह पर 10 M द्रव्यमान का एक त्रिकोणीय ब्लॉक रखा गया है | इसके शीर्ष पर M द्रव्यमान का एक छोटा गुटका रखा गया है | सभी सतहों को घर्षणरहित माने| इस स्थिति से इस निकाय को छोड़ दिया जाता है| जब गुटका जमीन पर पहुँचेगा उस समय ब्लॉक कितना विस्थापित हो चूका होगा ?
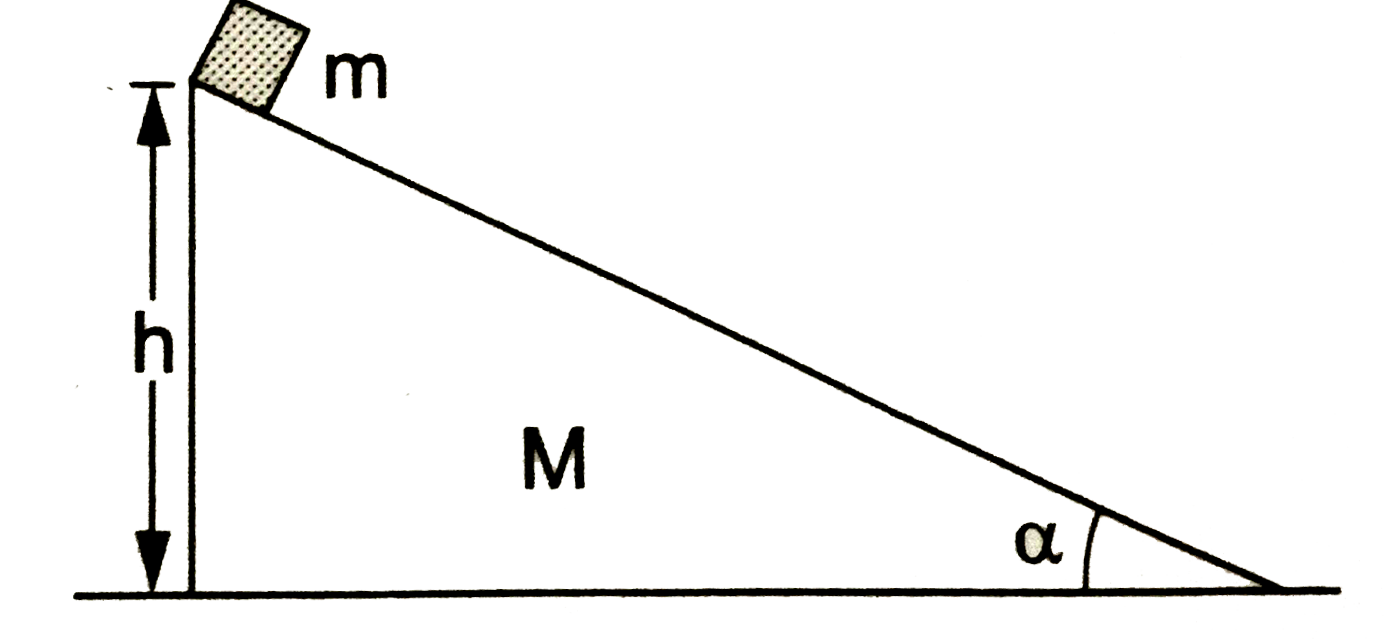
View Solutionm द्रव्यमान का एक गुटका M द्रव्यमान के एक त्रिभुजाकार गुटक पर रखा हुआ है, जो स्वयं एक क्षैतिज सतह पर रखा गया है चित्र
जब छोटा गुटका क्षैतिज सतह पर पहुँचता है, उस समय त्रिभुजाकार गुटके का वेग ज्ञात करें। सभी सतहों को घर्षणरहित मानें।
View SolutionA prism of mass M is placed on a horizontal surface. A block of mass m slides on the prism, which in tum slides on the horizontal surface. Assuming all surfaces to be frictionless, find the acceleration of block with respect to prism.

View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :

View SolutionFigure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mas m placed on a horizontal floor. The curved part of the surface shown is semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.

View Solution
