Particles of masses 1g, 2g, 3g ….100g are kept at the marks 1cm, 2cm, 3cm …., 100 cm respectively on a metre scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the metre scale.Solution in Tamil
The correct Answer is:B, C, D
Masses of 1gm, 2gm …………100 gm are kept at themarks 1cm, 2cm…………..100 cm on the xis resectively. A perpendicular axis is passed at the 50th particle.
Therefore on the L.H.S. of the axis there will be 49 particles and on the R.H.S there are 50 particles.
Consider the two particles at the position 49 cm and 51 cm.
Moment of inertia due to these two particles will be:
=49×(1)2+51×(1)2
=100×1=100gm−cm2
similarly if we consider 48th and 52nd term we will get 100×(2)2gm−cm2.
Threfore we wil get 49 such set and one lone particle at 100 cm. Threfoee totl moment of inertia
=100(12+22+32+........+492)+100(50)2
=100(1^2+2^2+3^2+..........+50^2)<br>=100xx(50xx51xx101)/6<br>=100x25xx17xx101<br>=100xx101xx425<br>=4292500gm-cm^2<br>=429kg-m^2=0.43kg-m^2
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -215videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises51videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises58videos
SIMPLE HARMONIC MOTION
Similar Questions
The axis of rotation of a purely rotating body
04:38View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
02:47View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
04:56View SolutionThree particles of masses 1 g, 2g and 3 g are kept at points (2cm,0), (0.6 cm), (4cm, 3cm) find moment of inertia of all three particles (in gm−cm(2)) about (a) x-axis
(b). Y-axis
(c). Z-axis.View SolutionAn uniform metre scale of weight 50g is balanced at 60cm mark, when a weight of 15g is suspended at 10cm mark. Where must a weight 100g be suspended to balance metre scale.
02:26View SolutionThree particles of masses 1gm,2gm&3gm are at 1cm,2cm&3cm from the axis of rotation respectively then the moment of inertia of the system & radius of gyration of the system respectively are …. gmcm2 and ….. cm
10:18View SolutionWeights of 1g, 2g,...., 100g are suspended from the 1-cm, 2-cm,......, 100-cm marks respectively of a light meter scale. Where should it be supported for the system to be in equilibrium ?
03:25View SolutionTwo masses of 3 kg and 5 kg are placed at 30 cm and 70 cm marks respectively on a light wooden meter scale, as shown in Fig. 8.51. what will the moment of inertia of the system about an axis through (i) 0 cm mark and (ii) 100 cm mark, and perpendicular to the meter scale?
 02:18View Solution
02:18View Solution10gm,20gm,30gm,…..,1000gm द्रव्यमान के कण एक नगण्य भार वाले मीटर स्केल के क्रमश: 1cm,2cm,3cm,……,100cm वाले निशानों पर रखे गए हैं । मीटर स्केल के लंबअर्द्धक के प्रति इस निकाय का जड़त्व आघूर्ण ज्ञात करें ।
02:18View SolutionA metre scale is balanced on a knife edge at its centre. When a coin of mass 15 g is kept at the 12 cm mark, the scale is found to be balanced at 45 cm. What is the mass of the metre scale?
03:42View SolutionA metre scale is balanced on a knife edge at its centre. When a mass of 10 kg is kept at the 12 cm mark, the scale is balanced at 45 cm. What is the mass of the metre scale?
02:06View SolutionTwo masses of 500 gram and 600 grams are attached to the 10 cm and 80 cm marks respectively of a light metre scale. The moment of inertia of this system about an axis passing through the centre of the scale will be
04:00View SolutionThe moment of inertia of a metre scale of mass 0.6 kg about an axis perpendicular to the scale and passing through 30 cm position on the scale is given by (Breadth of'the scale is negligible)
04:00View SolutionTwo masses of 3kg and 5kg are placed at 20cm and 70cm marks respectively on a light wooden meter scale. The M.I. of the system about an axis passing through 100 cm mark and perpendicular to the meter scale is
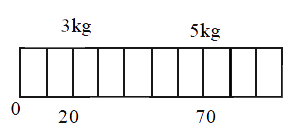 View Solution
View SolutionThree particles of masses 1g, 2g and 3g are at distances of 1cm, 2cm and 3cm from the axis of rotation. Find i) the moment of inertia of the system and ii) the radius of gyration of the system.
13:51View SolutionThree particles of masses 1g, 2g and 3g are at distances of 1cm, 2cm and 3cm from the axis of rotation. Find i) the moment of inertia of the system and ii) the radius of gyration of the system.
View Solution

