The moment of inertia of a uniform rod of mass 0.50 kg and length 1 m is 0.10 kg m^2 about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.Solution in Tamil
The correct Answer is:C, D
Length of the rod=1m, Mass of the rod
=0.5kg
Let at distance d from the centre the rod is moving.
Applying parallel axis therom, the moment of inertia about that point
→(ml212)+md2=0.10

→0.5×l212+0.5×d2=0.10 ltbr> →112+d2=0.2
→d2=0.118
d=0.342m from the centre
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -215videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises51videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises58videos
SIMPLE HARMONIC MOTION
Similar Questions
The axis of rotation of a purely rotating body
01:54View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
01:47View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
04:11View SolutionMoment of inertia of a uniform rod of mass m and length l is 712ml2 about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
03:48View SolutionCalculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
02:01View SolutionTwo uniform solid of masses m_(1) and m_(2) and radii r_(1) and r_(2) respectively, are connected at the ends of a uniform rod of length l and mass m . Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.
02:14View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I . The moment of inertia of the rod about an axis perpendicular to rod through its end point is
04:14View SolutionEach point mass 2 kg is connected at the end of each uniform rod of length 1m and mass 1kg. All the masses are in XY plane. Find the moment of inertia of system about Z-axis (in kg-m2).
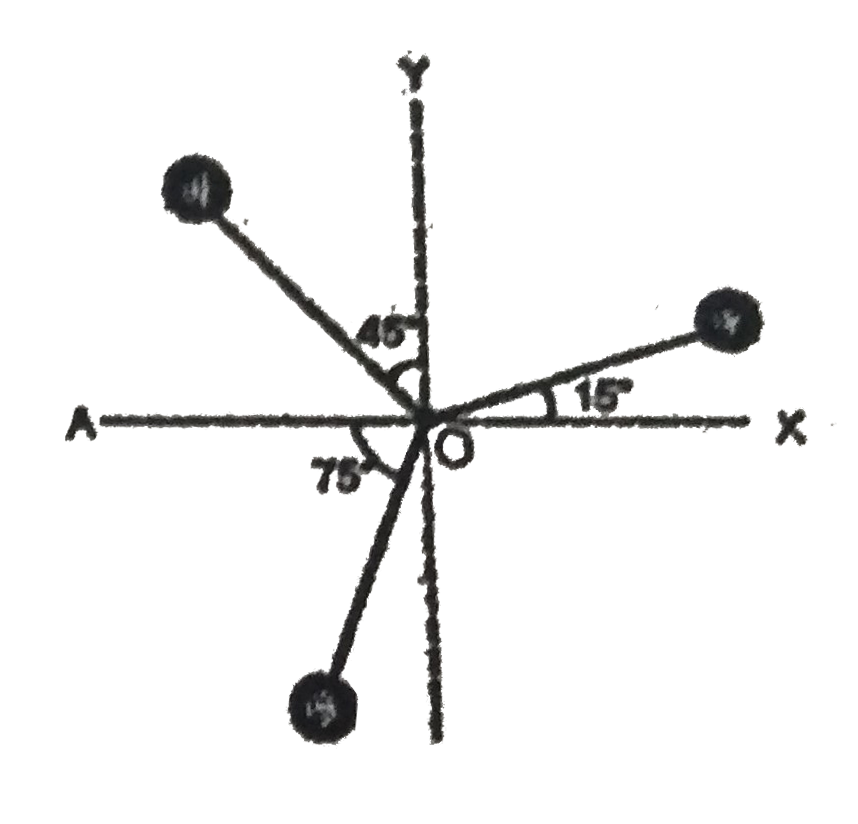 02:40View Solution
02:40View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
03:17View Solutionएक समरूप छड़ की लंबाई 1 m तथा द्रव्यमान 0.50kg है । किसी लंबवत रेखा के परितः छड़ का जड़त्व आघूर्ण 0.10kg.m2 है । छड़ के मध्यबिंदु से इस रेखा की दूरी ज्ञात कीजिए ।
03:45View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about axis perpendicular to the rod through its end point is
03:31View Solutionएक छड़ (लम्बाई l और द्रव्यमान m) का जड़त्व आघूर्ण उस अक्ष के सापेक्ष, जो छड़ की लम्बाई के लम्बवत् है तथा इस छड़ के मध्य बिन्दु और एक सिरे से बराबर दूरी पर स्थित बिन्दु से गुजरता है, है
View SolutionA uniform thin rod of 120 cm length and 1600 g mass is bent as shown in the figure. The moment of inertia of the bent rod about and axis passing through the point 'O' and perpendicular to the plane of the paper is . . . . . . kg -m^(2) .
02:24View SolutionFind the moment of inertia and radius of gyration of uniform cross-section rod of mass M and length l about an axis through a point at distance l3 from one end and perpendicular to the length of rod.
01:28View SolutionThe moment of inertia of a thin uniform rod of mass M and length l about an axis perpendicular to the rod through its centre is I. The moment of inertia of the rod through its end point is
02:26View SolutionMoment of inertia of a uniform rod of mass m and length l is 712ml2 about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
02:25View Solution

