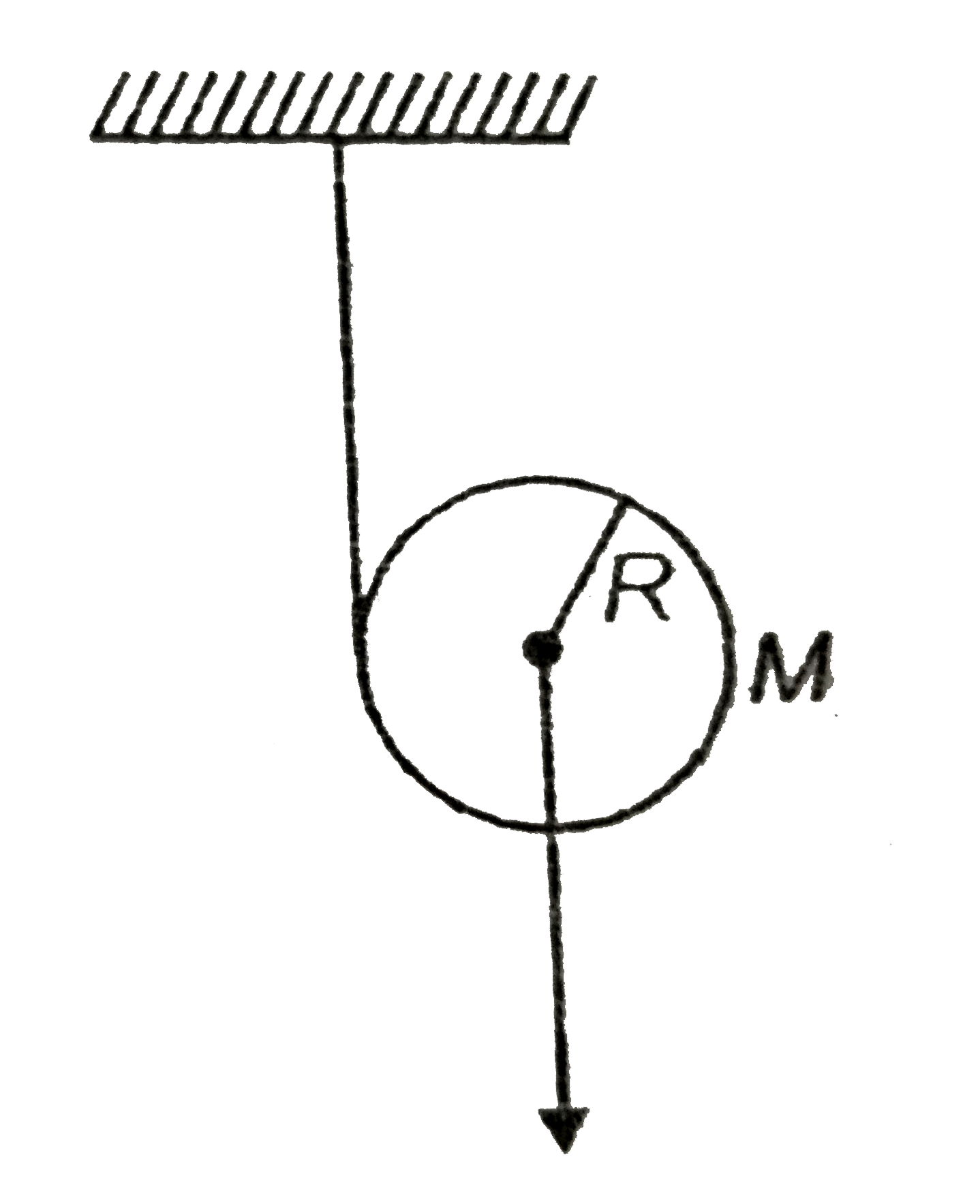
A string is wrapped over the edge a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.Solution in Tamil
The correct Answer is:B, C
Let the radius of the disc =R
Therefore according to the question and ure
mg−T=ma
and the toque about the centre
=T×R=1×α
→T×R=12mR2×aR
→T=12ma………..2
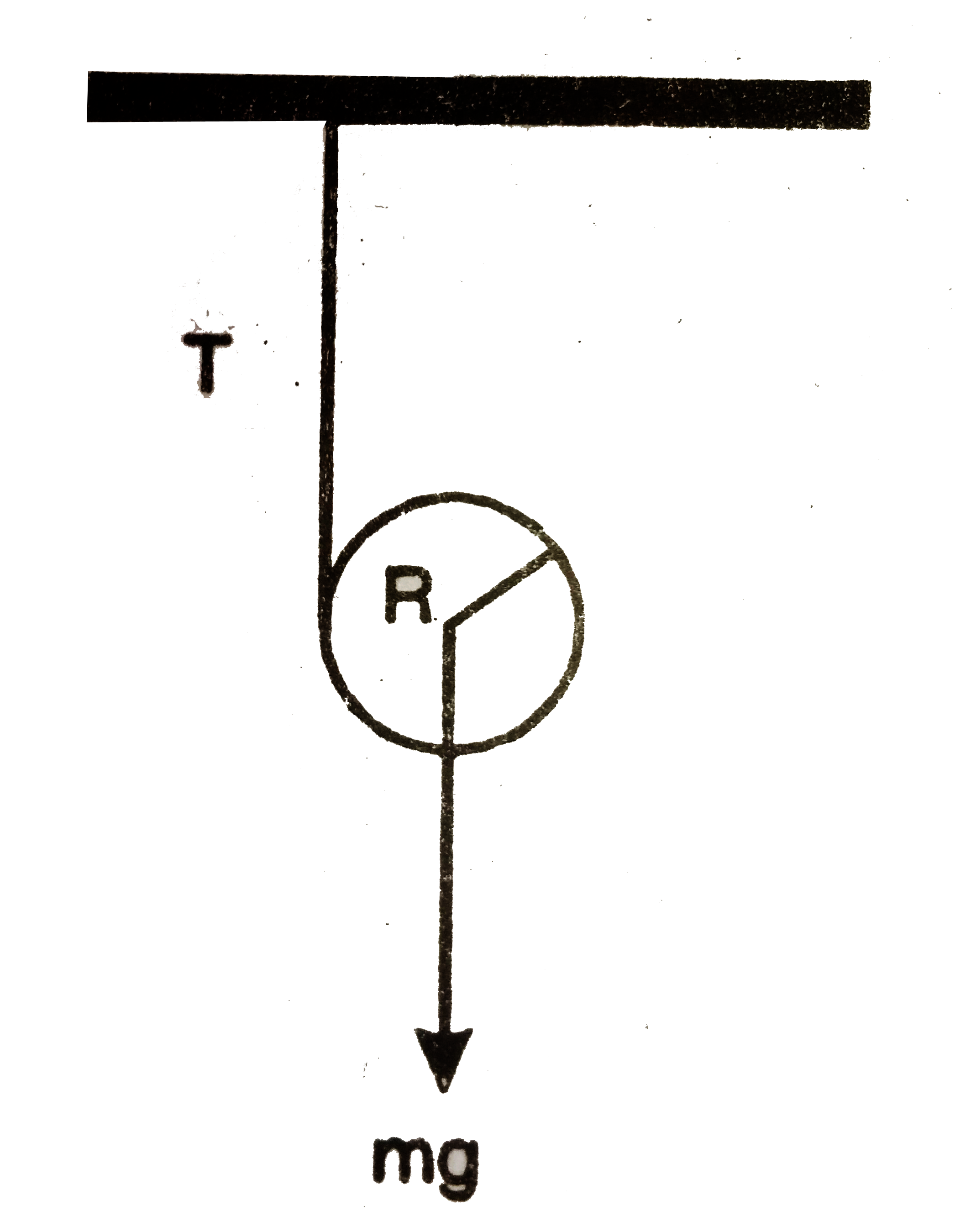
Putting this value in the equation 1 we get
→mg−12ma=ma
→mg=32ma
⇒a=2g3
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -215videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises51videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises58videos
SIMPLE HARMONIC MOTION
Similar Questions
The axis of rotation of a purely rotating body
07:54View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
10:07View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
01:31View SolutionA uniform disc of mas M and radius R is smoothly pivoted at O . A light iextensible string wrapped over the disc hangs a particle of mass m . If the system is released from rest, assuming that the string does not slide on the disc, find the angular speed of the disc as the function of time using impulse momentum equation.
02:40View SolutionIn the figure A and B are two blocks of mass 4kg and 2kg respectively attached to the two ends of light string passing overa disc C of mass 40kg and radius 0.1m. The disc is free to rotate about a fixed horizontal the string does not string does not slip over the disc. Find.
(i) The linear acceleration of mass B.
(ii) the number of revolutions made by the disc at the end of 10sec. from the start.
(iii) the tension in teh string segment supporting the block A.
 .View Solution
.View SolutionThe point P of a string is pulled up with an acceleration g. Then the acceleration of the hanging disc (w.r.t ground) over which the string is wrapped, is
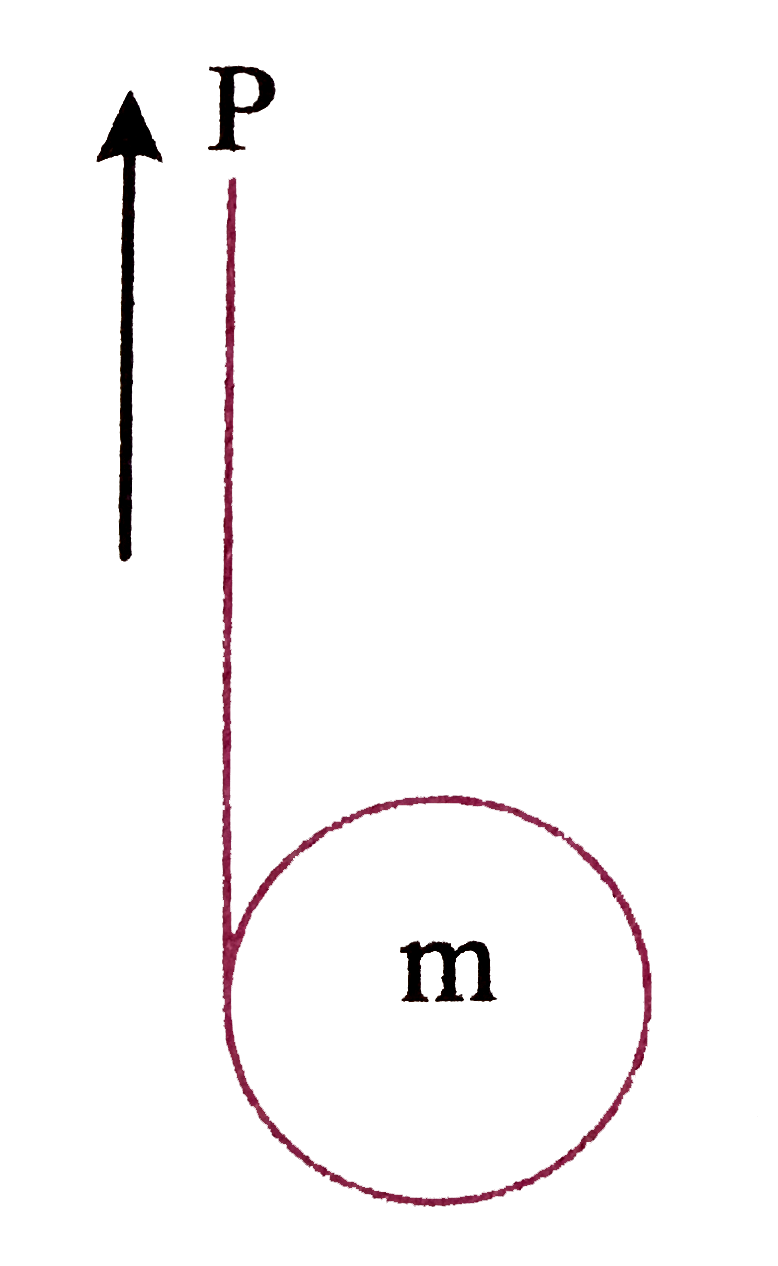 View Solution
View SolutionIn the figure shown a thin light inextensible string is wrapped around a uniform disc. One end of the strin is fixed to the ceiling of the lift and the other end is fied to the circumference of the disc. Acceleration 'a' of the lift is such that the centre of the disc not move with respect to ground. Find the value of ag. String does not slip on pulley.
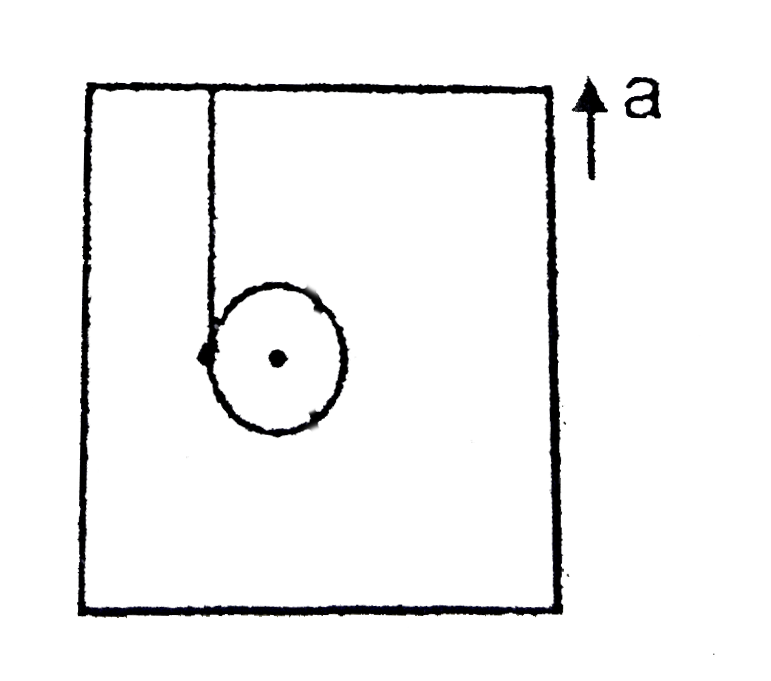 04:06View Solution
04:06View SolutionA string is wrapped on a uniform disc and the other end of the string connected to a wall. The system is placed on a smooth plane, inclined at an angle θ, with the string parallel to the plane, as shown in the figure. The acceleration of the disc is
 05:30View Solution
05:30View SolutionAn ideal inextensible string is wrapped over the disc of mass m and radius R. The other end of the string is connected to mass m. the string is passing over an ideal pulley A as shown in the figure. At any time t, mass m and disc are moving downward with acceleration of magnitude a1 and a2 respectively. The disc is rotating clockwise with angular acceleration of magnitude α . There is no slipping betweeb string and disc. choose the incorrect option
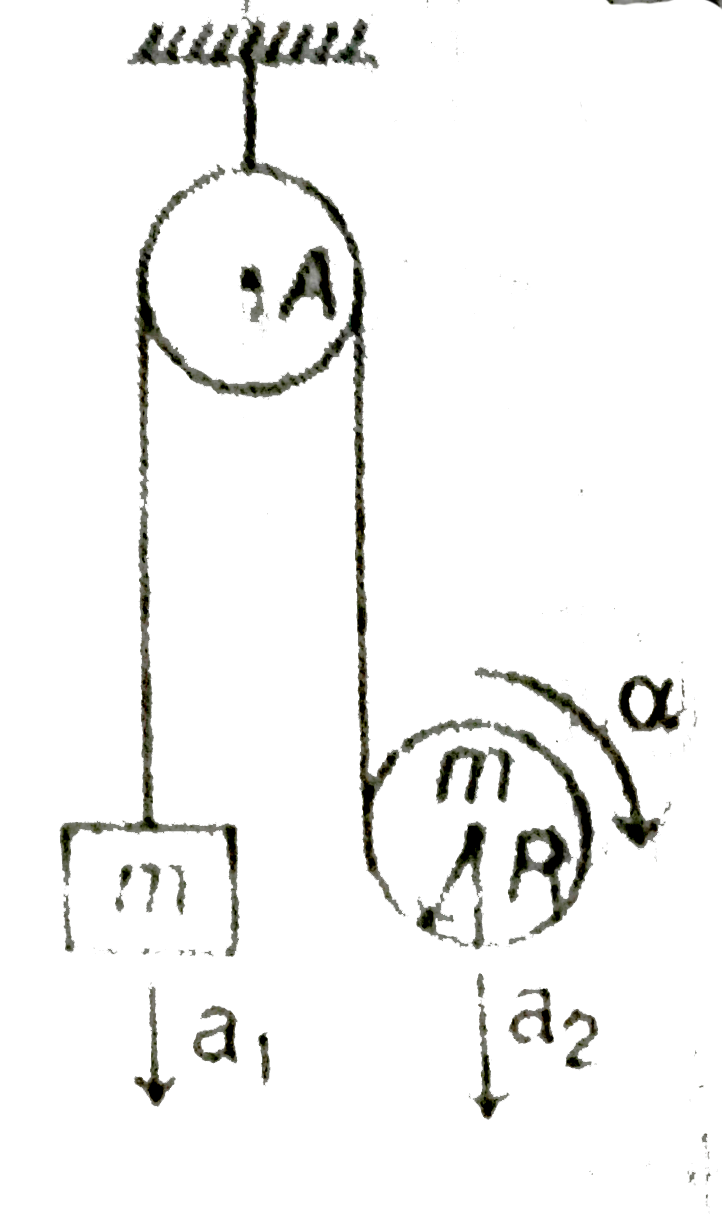 03:45View Solution
03:45View SolutionA disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
 02:51View Solution
02:51View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View SolutionString is wrapped over a pulley and free end is fixed to the ceiling as shown in figure. Mass of the pulley is m and its radius is R. Assume that pulley is identical to dise. Calculate acceleration of pulley as it is allowed to fall by unwinding the string. Assume that string does not slip over the pulley.
 View Solution
View SolutionA string is hanged to strong support O as shown in figure. It is wrapped to a disc of mass m and radius R at its other end. This string is weightless and unstretchable then find the linear acceleration of centre of mass of disc.
05:12View SolutionPassage - I : A massless inextensible string is wound arounf two indeentical discs A and B. Disc A is fixed at the centre but is free to rotate about its axis and B is free to fall down. If the string does not slip on either of the disc answer the following (Given mass of each disc is m and radius of each disc is R) The acceleration of disc B is
03:07View SolutionPassage - I : A massless inextensible string is wound arounf two indeentical discs A and B. Disc A is fixed at the centre but is free to rotate about its axis and B is free to fall down. If the string does not slip on either of the disc answer the following (Given mass of each disc is m and radius of each disc is R) The angular acceleration of disc A and tention in the string is
03:41View SolutionA string is wrapped on a uniform disc and the other end of the string connected to a wall. The system is placed on a smooth plane, inclined at an angle theta , with the string parallel to the plane, as shown in the figure. The acceleration of the disc is
04:32View Solution

