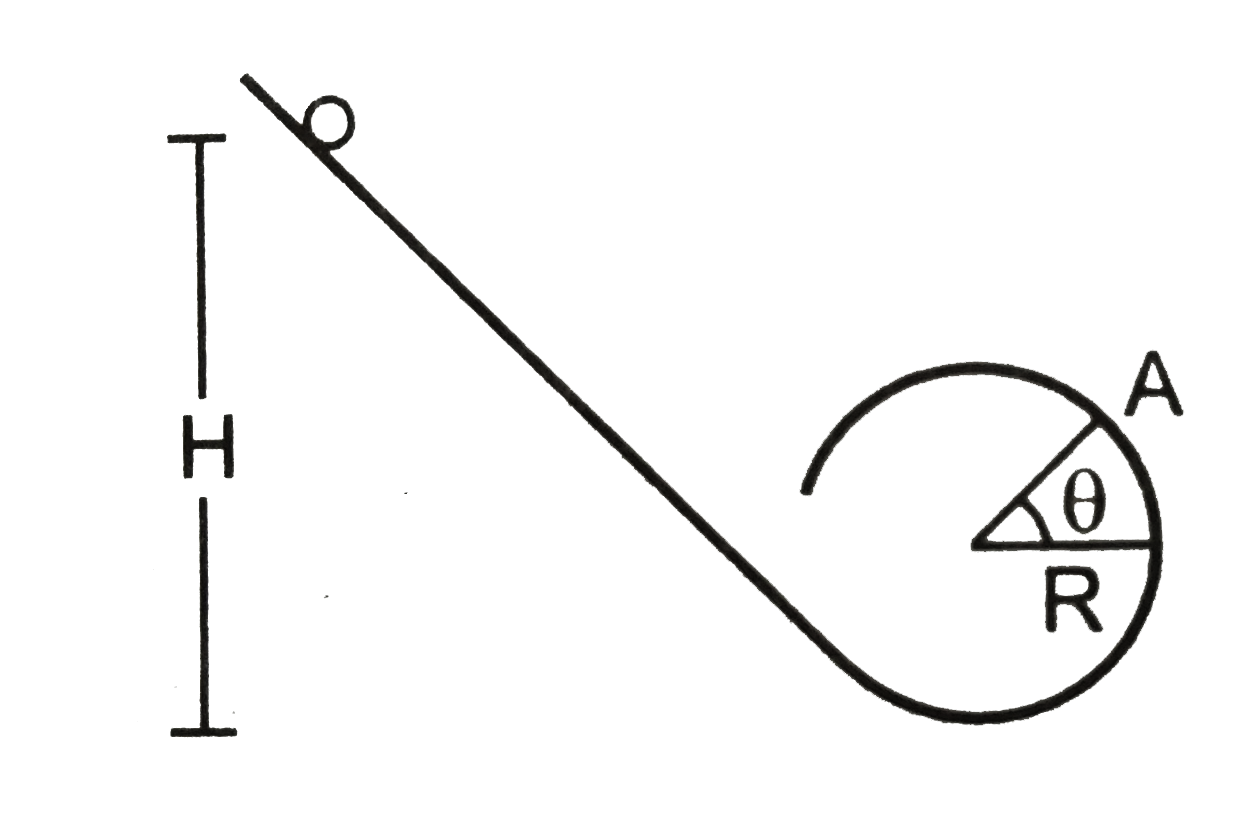
Figure shows a smasll sphereical bal of mass m rolling down the loop track. Thebasll is released on the linear portion at a verticla height H from the lowest point. The circular part show has a radius R.
a. find the kinetic energy of the ball when it is at a point where the radius makes an angle θ with the horizontal.
Find the radial and the tangential accelerations of the cente when the ball is at A. c. find the bnormal force and the frictionasl force acting on the ball if H=60 cm, R=10cm θ=0 and m=70 fg.
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B, C, D
a. Total kinetic energy
y=12mv2+12Iω2
therefore, according to the question
mgH=12mv2+12Iω2+mgR(1+sinθ)
→mgH−mgR(1+sinθ)
=12mv2+12Iω2
→12mv2+12Iω2=mg(H−R−Rsinθ)
b. To find the acceleratiohn components,
→12mv2+12Iω2=mg(H−R−Rsinθ)
→k710mv2=mg(H−R−Rsinθ)
→v2=107g(H−R−Rsinθ)
→v2=107g(H−R−Rsinθ).....i
→v2R=107(g[H−R)−Rsinθ])R
→v2R=(10g[(H−R)−Rsinθ)])R
−2vdvdt=−(107)gRcosθdthηdt
→ωRdvdt=−(57)gRcosθdthηdt
→dvdt=−(57)gcosθ
→ tangential acceleration
c. Normal force at thea=0
mv2R=(70100)×(107)×10{(0.6−0.1)0.1}
=5N
Friction force:
=f=mg−ma
−f=m(g−a)
m(10−57x10)
=0.07(10−57×10)
=1100(70−50)=0.2N
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -215videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises51videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises58videos
SIMPLE HARMONIC MOTION
Similar Questions
The axis of rotation of a purely rotating body
03:08View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
04:39View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
08:11View SolutionA small sphereical ball is released from a point at a height h on a rough track shown in figure. Assuming that it dow not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.
 09:52View Solution
09:52View SolutionFigure shows a smooth track, a part of which is a circle of radius r. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.
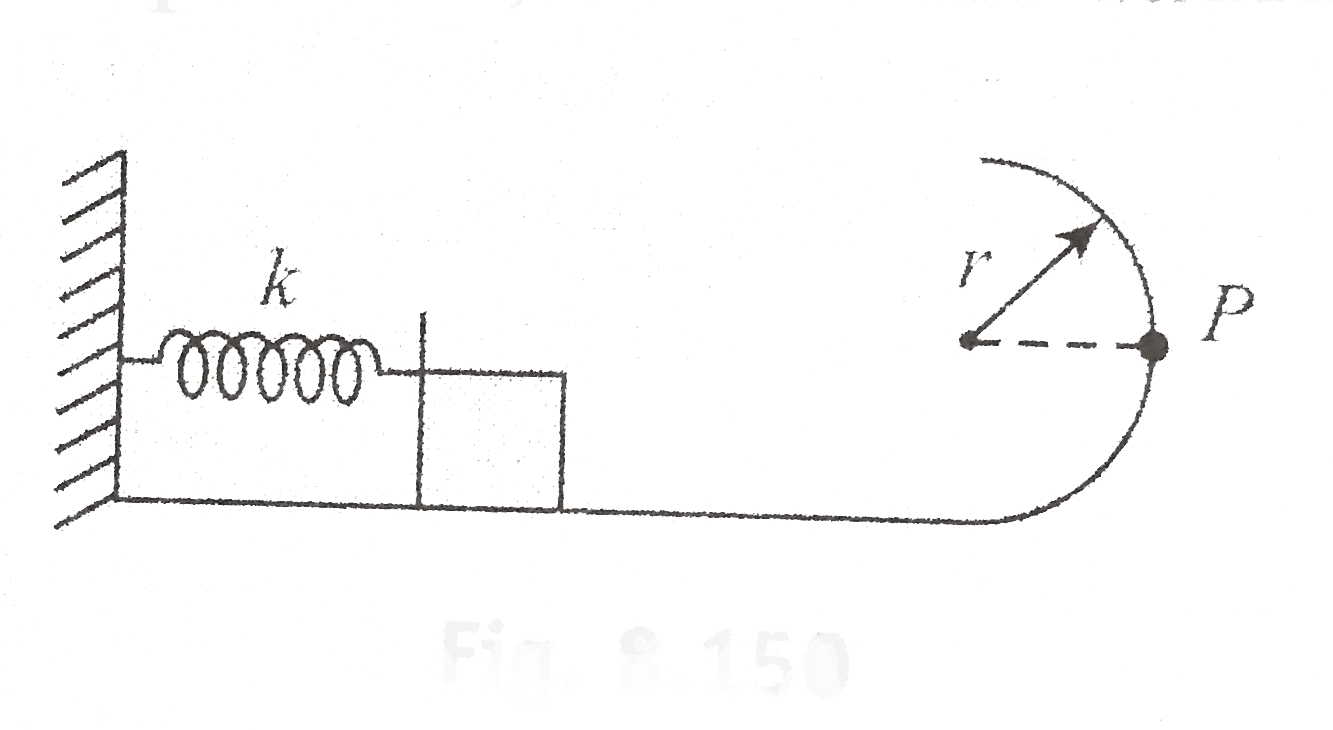 05:28View Solution
05:28View SolutionA small solid marble of mass M and radius r rolls down along the loop track, without slipping. Find the height h above the base, from where it has to start rolling down the incline such that the sphere just completes the vertical circular loop of radius R.
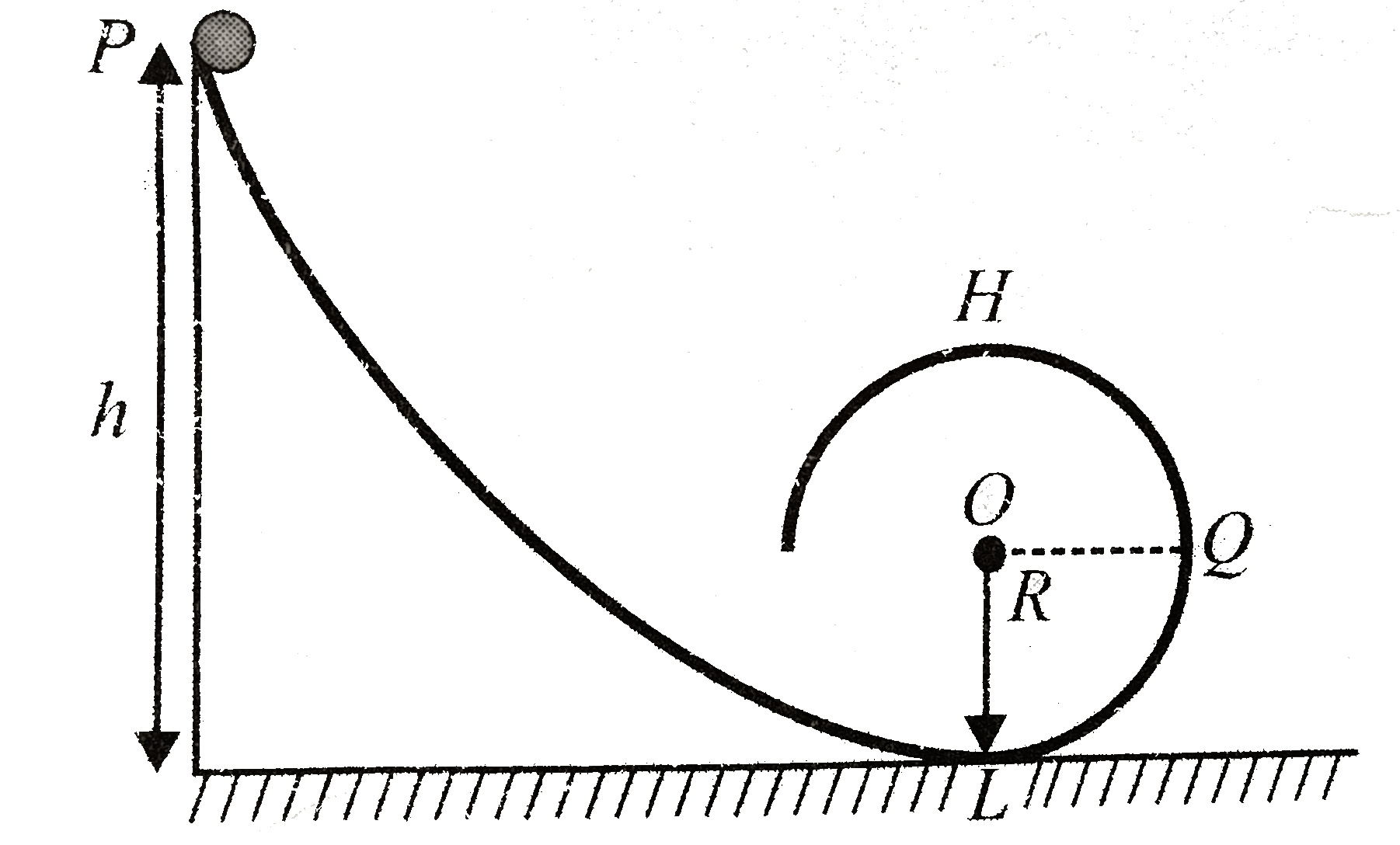 12:58View Solution
12:58View SolutionA block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A . Find the velocity of sphere and track , when the sphere reaches B .
03:19View SolutionAs shown in the figure, a small is released from a certain height h which has to perform circular motion on a vertical smooth track of radius 4 m. the track is absent between point A and B. Calculate the height (in m) from where the ball has to be released so that it will reach at highest point B of the circular track
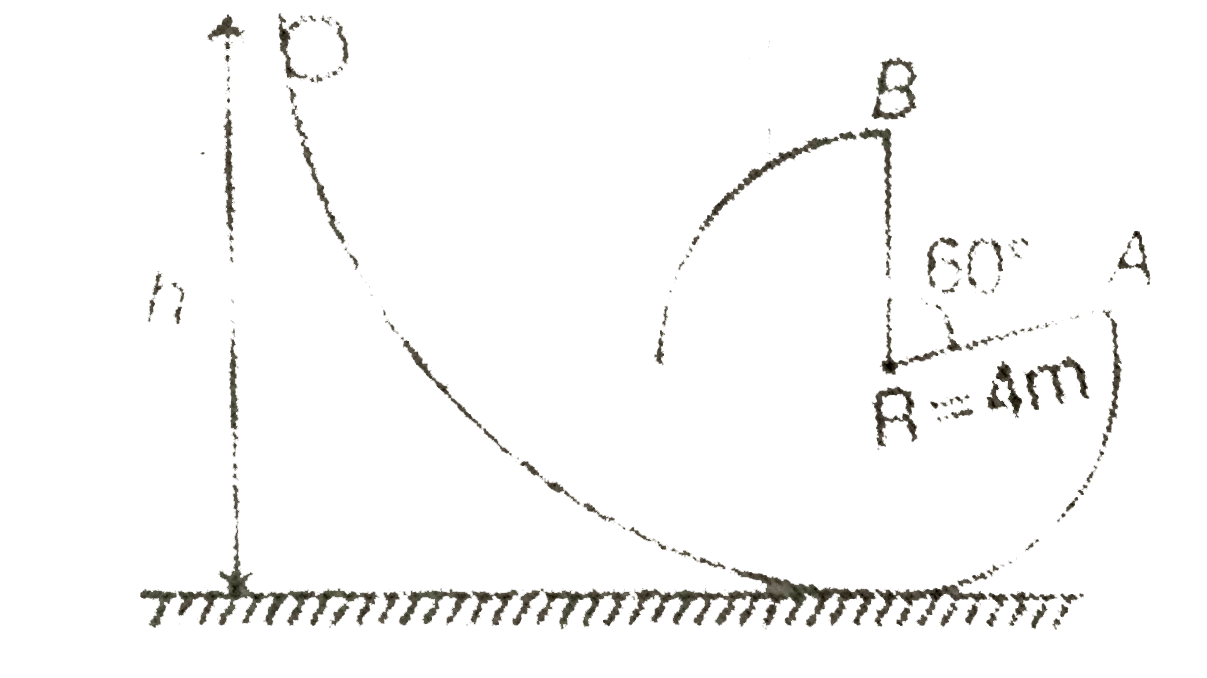 04:22View Solution
04:22View Solutionचित्र में m द्रव्यमान का एक गोलाकार बॉल लूप आकृति के पथ पर नीचे की ओर लुढ़क रहा है। बॉल को पथ के रेखीय भाग पर पथ के निम्नतम बिंदु से H ऊँचाई से छोड़ा गया है। चित्र में दिखाए गए पथ के वृत्ताकार भाग की त्रिज्या R है।
(a) बिंदु A पर त्रिज्या क्षैतिज से θ कोण बनाती है। बॉल जब बिंदु A पर पहुँचता है तब उसकी गतिज ऊर्जा ज्ञात करे।
(b) जब बॉल A पर है, उस समय इसके त्रिज्यीय तथा स्पर्शरेखीय त्वरण ज्ञात करे।
(c) यदि H=60cm,R=10cm,θ=0∘ तथा m=70g हो, तो बॉल पर लगनेवाले अभिलंब बल तथा घर्षण बल के मान ज्ञात करे।
 View Solution
View SolutionA small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
View SolutionA small spherical ball is released from a point at a height h on a rough track shown in figure. Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.
 02:17View Solution
02:17View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R=(R=97m). It makes small oscillations about the lowest point. Find the time period.
08:24View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R=(R=97m). It makes small oscillations about the lowest point. Find the time period.
10:39View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View SolutionA block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.
 02:41View Solution
02:41View SolutionAs shown in the figure, a small is released from a certain height h which has to perform circular motion on a vertical smooth track of radius 4 m. the track is absent between point A and B. Calculate the height (in m) from where the ball has to be released so that it will reach at highest point B of the circular track
02:43View Solution

