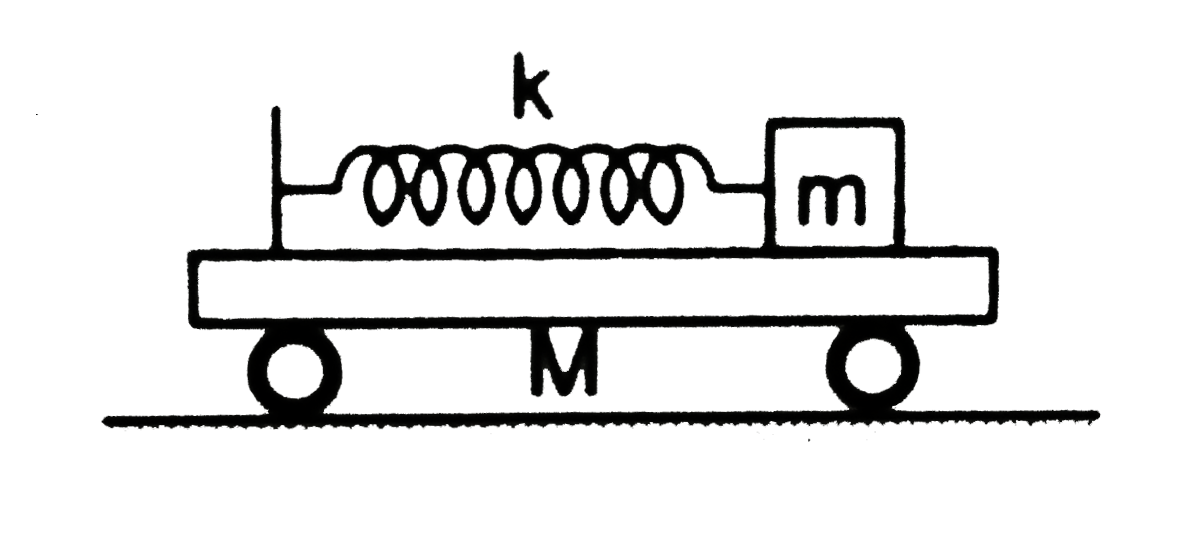
All the surfaces shown in figure are frictionless. The mass of the car is M, that of the block is mk and the spring has spring constant. Initialy the car and the block are at rest and the spring is stretched through a length x0 when the system is released. a. Find the amplitude of the simple harmonic motion of the blocks and of the car as seen from the road. b. Find the time periods of the two simple harmonic motions.
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B
Let the amplitude of oscillation of m and M be x1andx2 respectively.
a. From law of conservation of momentum mx1=Mx2 ………1
[Block and mass oscillates in opposite direction bt xp→ stretched part]. From equation 1 and equation 2<br>:. x_0=x_1+m/Mx_1<br>=((M+m)/M)x<br>so, x_2=x_0-x_1<br>x_0[1-M/(M+m)]<br>=(mx_0)/(M+m)respectively<br>b.Atanyposition,≤tthevelocitybev_1 and v_2respectively.Herev_1 velocity of m'withrespect→M.Bye≠rgymethod,<br>TotalE≠rgy=Constant<br>1/2mv_2^2+1/2m(v_1-v_2)^2+1/2k(x_1+x_2)^2<br>>=constant.......3<br>[v_1-v-2=|o|lutevelocityofmassmasseenomtheroad]<br>Mx_2=mx_1<br>rarr x_1=(M/m)x_2.........4<br>Mv_2=m(v_1-v_2)<br>rarr (v_1-v_2)=(M/m)v_2..........5<br>Pu∈gtheabovevalues∈equation3we≥t<br>1/2Mv_2^I2+1/2m M/m^2 v_2^2+1/2kx_2^2(1+M/m)<br>:.M(1+M/m)v_2^2+k(1+M/m)x_2^2=constant<br>rarr Mv_2^2+k(1+M/m)x_2^2=constant<br>Tak∈gderivativeof⊥hss,<br>M_2v_2(dv_2)/(dt)=k((M+m)/m)2x_2(dx_2)/(dt)=0<br>rarr ma_2+k((M+m)/m)x_2=0<br>[because v_2=(dx_2)/(dt)]<br>a_2/x_2=(-kM+m)/(Mm)omega^2<br>:. omega=(-k(M+m))/(Mm)<br>Sotimeperiod<br>T=2pi sqrt((Mm)/(M+m))
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-216videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises86videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises32videos
SOME MECHANICAL PROPERTIES OF MATTER
Similar Questions
Select the correct statements
02:45View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
11:06View SolutionA load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
01:55View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 . 02:29View Solution
. 02:29View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
 .04:31View Solution
.04:31View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
01:43View SolutionBlock A of mass m is placed on a plank B . A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initialy spring is in the natural length, and the system is at rest. Find the maximum compression in the spring, if the plank B is moved with a constant acceleration 'a' . (All the surface are smooth) :
01:50View SolutionBlocks A&B of mass m each are connected with spring of constant k both blocks lie on frictionless ground and are imparted horizontal velocity v as shown when spring is unstretched find the maximum stretch of spring.
05:57View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 19:15View Solution
19:15View SolutionTwo blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35 N/m . Find the maximum compression in the spring.
02:44View Solutionचित्र में दो गुटके दिखाए गए हैं जिनके द्रव्यमान m तथा M है। ये गुटके एक घर्षणरहित क्षैतिज सतह पर रखे हैं तथा k स्प्रिंग नियतांक वाले एक स्प्रिंग से जुड़े हैं। प्रारंभ में स्प्रिंग अपनी स्वाभाविक लंबाई में है तथा गुटके स्थिर हैं। अब एक अचर बल F, द्रव्यमान M वाले गुटके पर लगना प्रारंभ करता है। स्प्रिंग की लंबाई में अधिकतम वृद्धि निकालें।
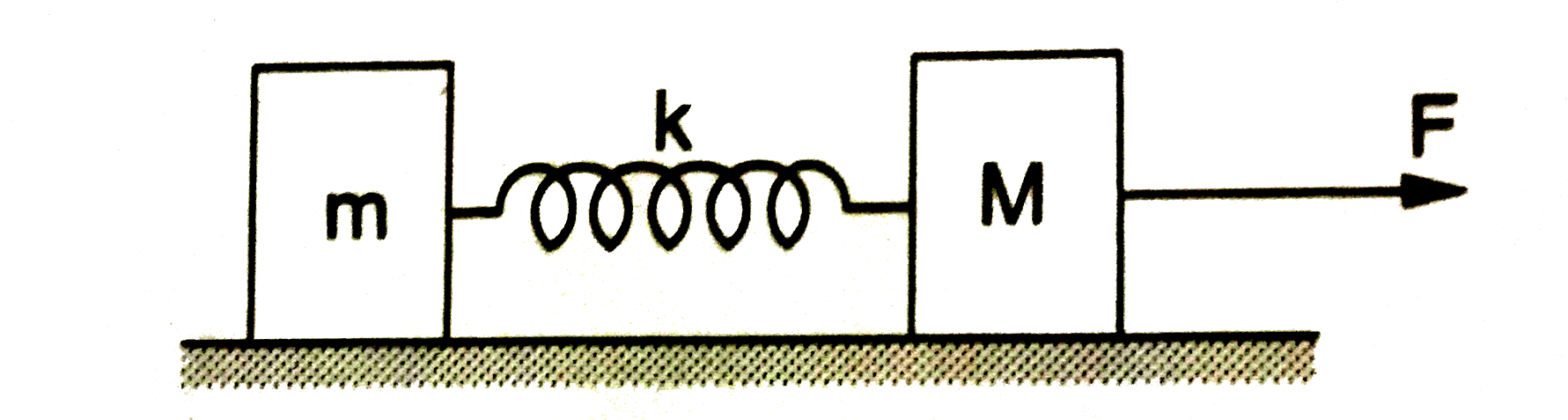 View Solution
View Solutionचित्र 21.EIS में दिखाई गई सभी सतहे घर्षणरहित है, कार का द्रव्यमान M है, ब्लॉक का द्रव्यमान m है तथा स्प्रिंग नियतांक k है। प्रारंभ में कार तथा ब्लॉक विराम में हैं तथा स्प्रिंग अपनी स्वाभाविक लंबाई से x0 दूरी खिचा हुआ है। इस स्थिति से निकाय को गति करने के लिए छोड़ दिया जाता है। (a) दिखाएँ कि सड़क के फ्रेम से बलॉक तथा गाड़ी की गतियाँ सरल आवर्त गतयों है तथा इनके आयाम निकाले। (b) दोनों गतियों के आवर्तकाल निकालें
 02:22View Solution
02:22View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m
04:42View SolutionIn the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.
 08:05View Solution
08:05View SolutionTwo springs are connected to a block of mass M is placed on a frictionless surface as shown in figure. If both springs have a spring constant k, the frequency of oscillation of the block is………
 02:24View Solution
02:24View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 . 02:39View Solution
. 02:39View Solution

