In the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
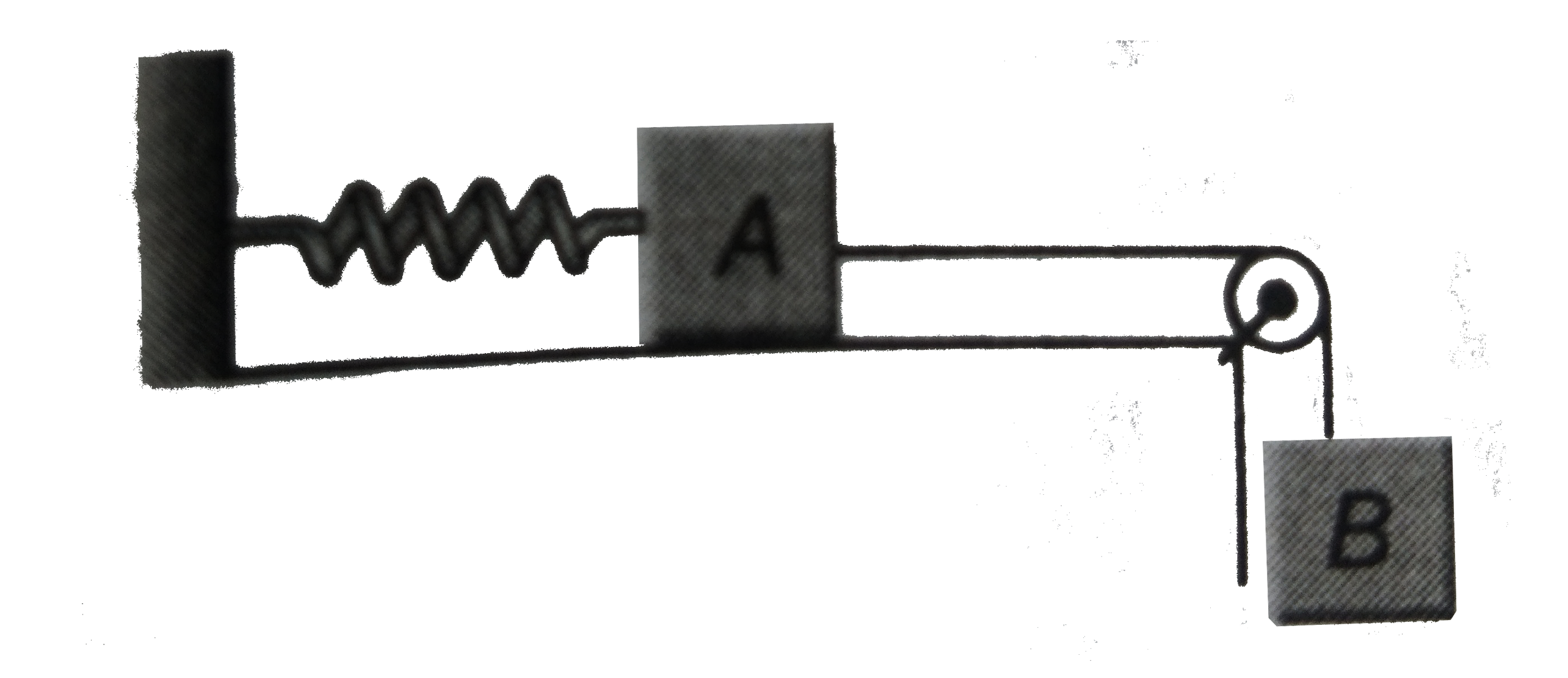 .
.
The maximum extension of the spring is 4mgk.
The speed of A when extension in spring is 2mgk is 2g√2m3k.
The acceleration of block B when the extension in the spring is maximum, is 23g
Tension in the thread for extension of 2mgk in spring is mg
The correct Answer is:A
(a) Decrease in potential energy of B= increase in spring potential
∴2mgxm=12kx2m
∴xm4mgk
(b) Ei=Ef
0=12(m+2m)v2+12×k×(2mgk)2
−(2mg)(2mgk)
∴v=2g√m3k
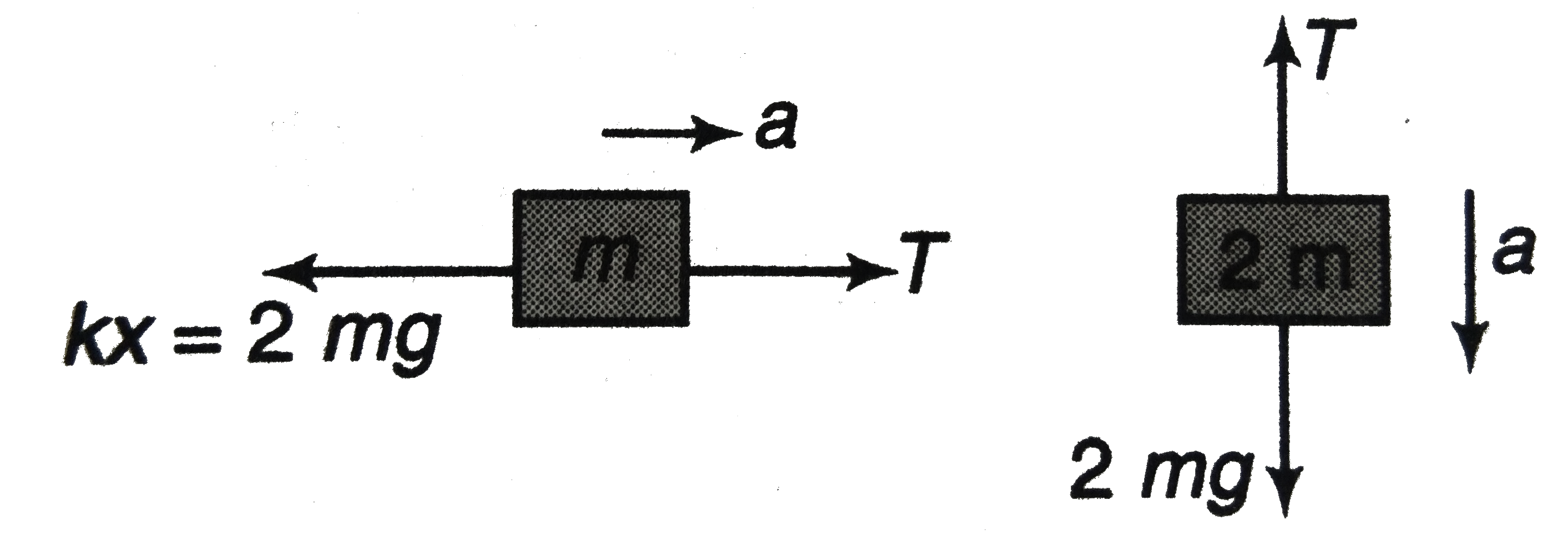
(c) a=kxm−2mg2m(upwards)
=k(4mgk)−2mg2m=g
(d)T−2mg=ma....(i)
2mg−T=2mg......(ii)
Solving these two equations, we get
a=0 and T=2mg
 .
.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Subjective15videos
WORK, ENERGY & POWER
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 objective30videos
WORK, ENERGY & POWER
- BOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
Consider the situation shown in figure.
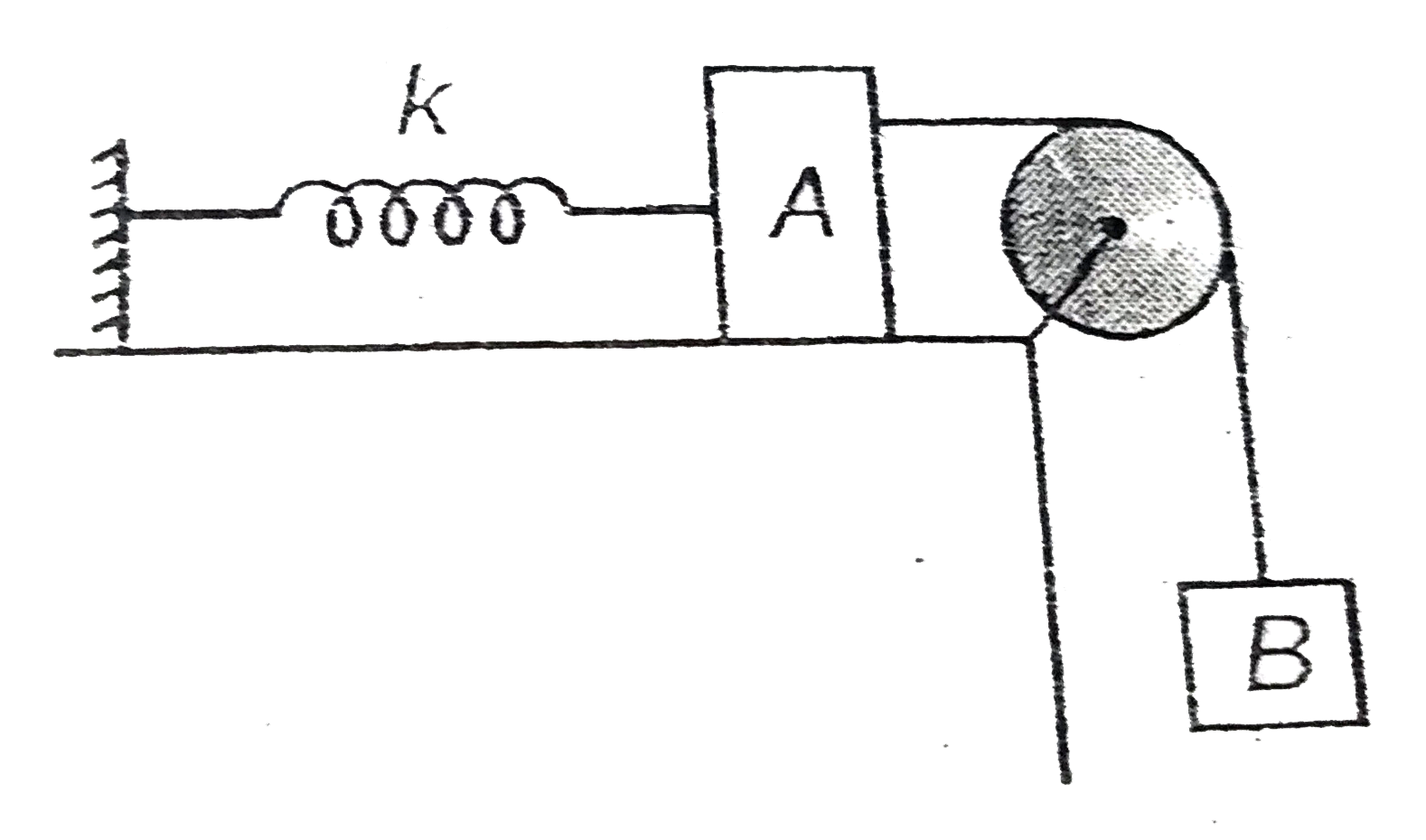
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the shown diagram mass of A is m and that of B is 2 m. All the surfaces are smooth. System is released from rest with spring unstretched. Then, the maximum extension (xm) in spring will be:
 AmgkB2mgkC3mgkD4mgk
AmgkB2mgkC3mgkD4mgk - Question 2 - Select One
A block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4 - Question 3 - Select One
A block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
AMF(m+M)BmFMC(M+m)FmDmF(m+M)
A block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.
 View Solution
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View SolutionA block of mass m is attached with a massless spring of force constant k. The block is placed over a fixed rought inclined surface for which the coefficient of friction is μ=34 . The block of mass m is initially at rest . The block is mass M is released from rest with spring in unstretched state. The minimum value of M required to move the block up the plane is ( neglect mass of string and pulley and friction in pulley )
 View Solution
View SolutionA block of mass 2M is attached to a massless spring with spring-constant k. This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a1a2 and a3 as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x0 Which of the following option(s) is(are) correct? [g is the acceleration due to gravity. Neglect friction]
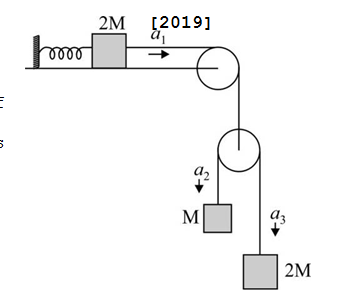 View Solution
View SolutionIn the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.
 View Solution
View Solution

