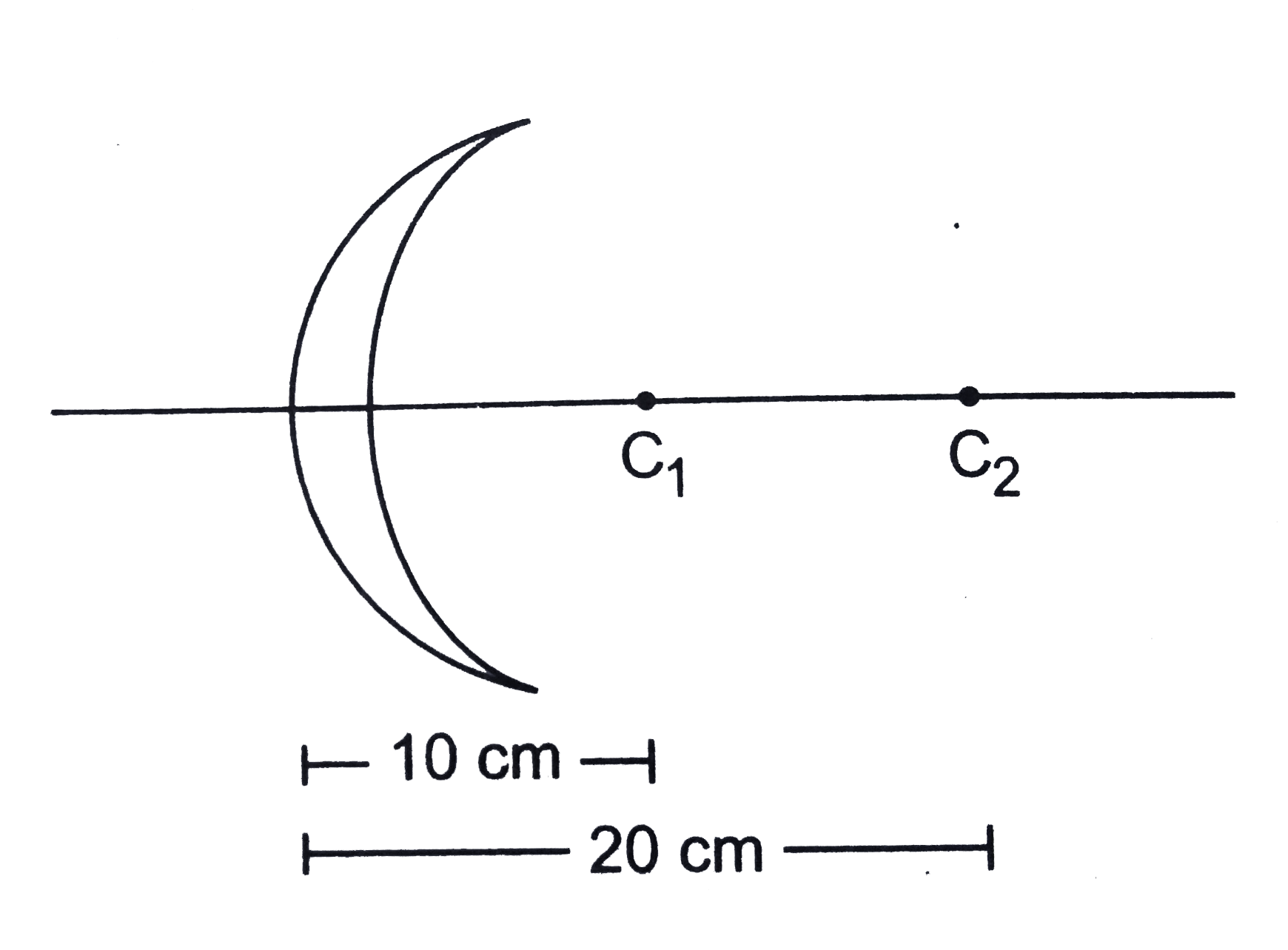
Calculate the focal length of the thin lens shown infigure. The pionts C1andC2 denote the centres of curvature.
 Solution in Tamil
Solution in Tamil
As is clear from the ure boththe radii of curvature are positive. Thus, R1=+10cm and R2=+20cm. The focal length is given by
1f=(μ−1)(1R1−1R2)
=(1.5−1)(110cm−120cm)
=0.5×120cm=140cm
orf=40cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMACHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
19 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMACHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -1
18 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMACHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercises
79 Videos
- GAUSS LAWBOOK - HC VERMACHAPTER - GAUSS LAWEXERCISE - Exercises
24 Videos
- LIGHT WAVESBOOK - HC VERMACHAPTER - LIGHT WAVESEXERCISE - Exercises
41 Videos
Similar Questions
Is the formula "Real depth/Apparent depth =μ. valid if viewed from a position quite away from the normal ?
View SolutionA point source of light is placed in front of a plane mirror.
View SolutionA concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
View SolutionThe electric field in a region is given by →E=35E0→i+45E0→j with E0=2.0×103NC−1. Find the flux of this field through a recatngular surface of area 0.2m2 parallel to the y-z plane.
View SolutionFind the range of frequency of light that is visible to an average human being (400nm<λ<700nm)
View SolutionIn the figure, light is incident on a thin lens as shown. The radius of curvature for both the surfaces is R. Determine the focal length of this system.
View SolutionFocal length of a thin lens in air is 10cm. Now, medium on one side of the lens is replaced by a medium of refractive inidex μ=2. The radius of curvature of the surface of lens, in contact with the medium, is 20cm. Find the new focal length.
View SolutionShows a thin lens with centres of curvature C1andC2. If μ=1.5, what is its focal length ?
 .
.
View SolutionFig. 6(b).54. shows a thin lens with centres of curvature C_(1) and C_(2) . If mu = 1.5 , what is its focal length ?
View SolutionThe focal length of a thin convex lens for red and violet colour are 44.6cm and 42.5cm. Calculate focal length for the mean colour and dispersive power of the lens.
View SolutionDefine focal length and radius of curvature of a concave lens.
View SolutionDefine centre of curvature.
View SolutionCalculate the focal length of the lens shown in the figure.
View SolutionA thin equi-convex lens having radius of curvature 10 cm is placed as shown in figure. Calculate focal length of the lens, if parallel rays are incident as shown.
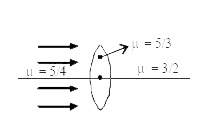
View SolutionA thin lens with centres of curvature C1andC2 is shown in the figure given below. If the refractive index of material of lens is 1.5, calculate the focal length in cm.

View SolutionFocal length of thin lens ......
View Solution
