A ball is kept at a height h above the surface of a heavy transparent sphere made of a material of refractive index The radius of the sphere is R. At t = 0, the ball is dropped to fall normally on the sphere. Find the speed of the image formed as a function of time for t<√2hg. Consider only the image by a single refraction. Solution in Tamil
The correct Answer is:A, B
At time t<√2hg,u=h−12>2,μ1=1

mu/v+g/u=(mu-1)/R<br>mu/v=(mu-1)/R-1/mu=(mu(mu-1)-R)/(muR)<br>v/mu=(uR)/(u(mu-1)-R)<br>=((h-1/2g^2)R)/((h-1/2gt^2)(mu-1)-R)<br>1/muxx(dv)/(dt)=[R(-gt)[(h-1/2gt^2)(mu-1)-R]]<br>+[R(-gt)(h-1/2gt^2)(mu-1)-R]^2<br>(R(h-1/2gt^2))gt(mu-1)<br>(dv)/(dt)xx1/mu=(gtxxR^2)/([(h-1/2gt^2)(mu-1)-R]^2)<br>(dv)/(dt)=(gtxxR^2)/([(h-1/2gt^2)(mu-1)-R]^2)<br>=μ>R2[(h−12>2)(μ−1)−R]2
Topper's Solved these Questions
Similar Questions
If the light moving in a straight line bends by a small but fixed angle it may be a case of
View SolutionThe electric field in a region is given by →E=35E0→i+45E0→j with E0=2.0×103NC−1. Find the flux of this field through a recatngular surface of area 0.2m2 parallel to the y-z plane.
View SolutionFind the range of frequency of light that is visible to an average human being (400nm<λ<700nm)
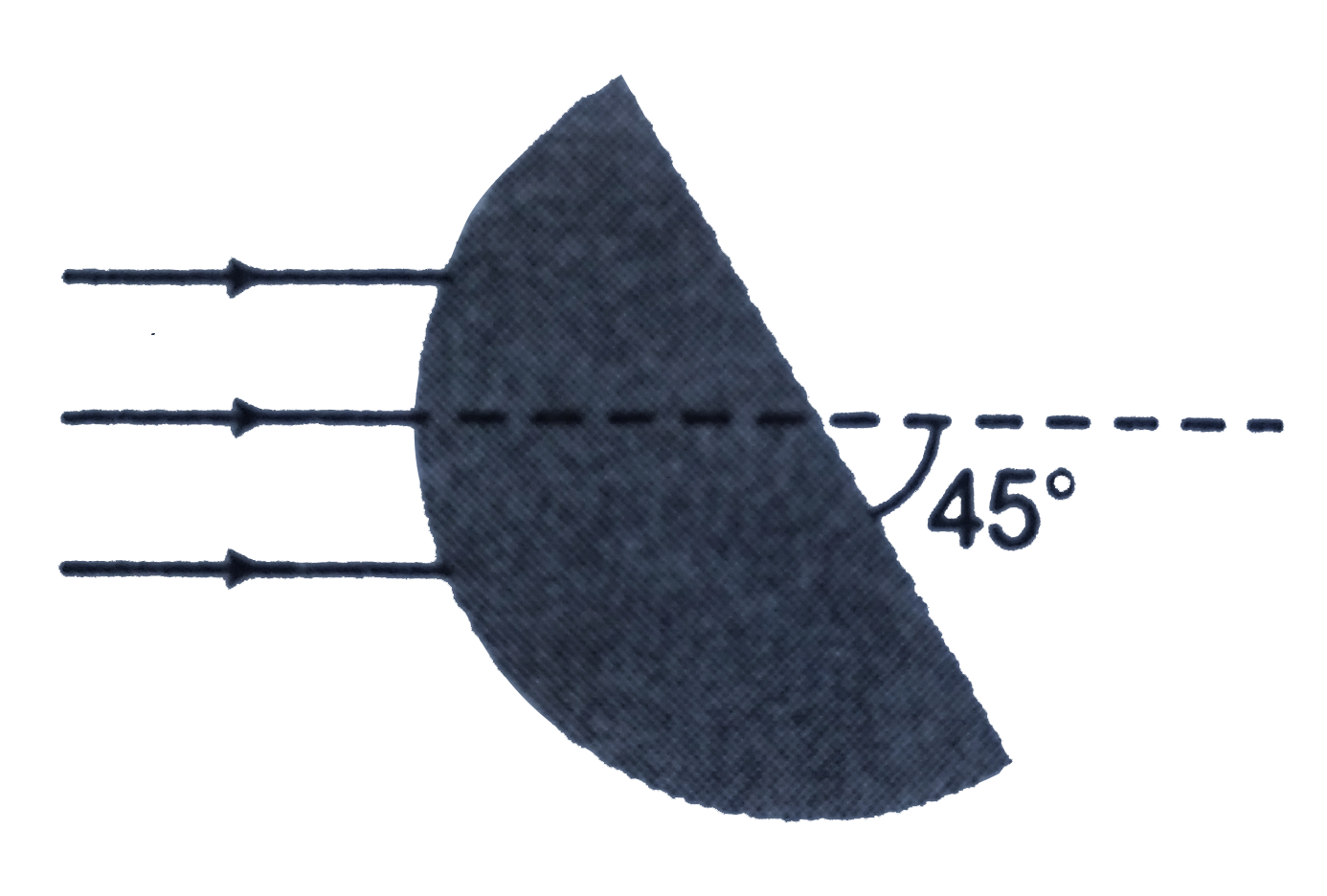
View SolutionA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
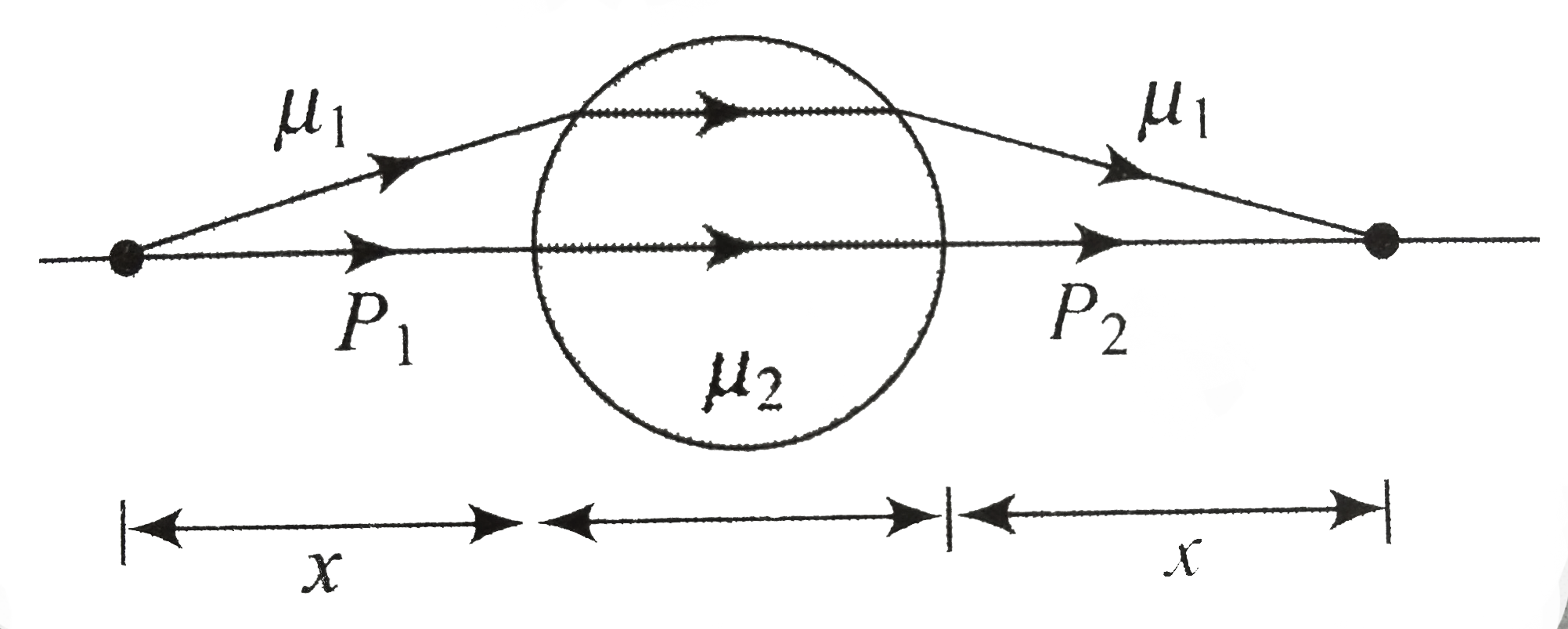
View SolutionA sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
View SolutionA narrow parallel beam of light falls on a glass sphere of radius R and refractive index mu at normal incidence. The distance of the image from the outer edge is given by-
View SolutionA transparent sphere of radius R and refractie index mu is kept in air. At what distance from the surface of the sphere shold a point object be placed so as to form a rea image at the same distance from the sphere?
View SolutionFigure shows a point object placed in front of a transparent sphere of radius 20 cm and refractive index 1.5. The sphere forms an image due to refraction at surface I followed by refraction at surface II. The sphere is kept in air and the object is located at distance x from P_(1) . It is found that for x gt x_(1) , the image formed due to refraction at surface I is real, the final image formed by the sphere is also real and forms to the right of P_(2) . For x_(2) lt x lt x_(1) , the image formed by surface I is virtual while the final image formed by the sphere is real and forms to the right of P_(2) . However for x lt x_(2) , the image formed by surface I and also the final image formed by the sphere are virtual. It is also found that the final image is virtual if the distance of image formed by surface I from P_(2) is less than y. The object is now moved away from the sphere so that x becomes large and say, x to oo . In the given sphere is replaced by another one of the same radius but of refractive index 2.5, the final image is formed at distance y_(2) from P_(2) . For the object placed at x to oo , a sphere of the same radius but of refractive index 2.5 forms an image at distance y_(2) from P_(2)
View SolutionA hollow sphere made of a transparent material of refractive index 1.5 has a small mark on its surface as shown. The mark is observed from the farther side. Find the distance of the image of mark from the centre of the sphere.

View Solutionप्रकाश की एक पतली समानांतर बीम r त्रिज्या के एक पारदर्शी गोले पर लंबवत पड़ती हैं । गोले के पदार्थ का अपवर्तनांक कितना होना चाहिए ताकि यह बीम गोले की सतह पर फोकस हो ।
View SolutionA small object is enclosed in a transparent solid sphere of radius 8 cm. the object is situated at 2 cm from the centre of the sphere. If its image appears to be at 3.2 cm from the nearest side, then the refractive index of the material of the sphere is
View SolutionA ray of light falls on a transparent sphere sphere with centre C as shown in the figure. The ray emerges from the sphere parallel to the line AB. Find the angle of refraction at A, if refractive index of the material of the sphere is sqrt(3) .
View SolutionA ball is kept at a height h above the surface of a heavy transparent sphere made of a material of refractive index μ. The radius of the sphere is R. At t=0 the ball is dropped to fall normally on the sphere. For t<√2hg and by a single refraction, what is the speed of image as a function of time?
View SolutionA parallel beam falls on solid glass sphere of radius R and refractive index mu . What is the distance of final image after refractioin from two surfaces of sphere? What is the condition for the image to be real?
View SolutionA sphere of radius R of material of refractive index mu_3 . Where should an object be placed so that a real image is formed equidistant from the sphere?
View SolutionA transparent solid sphere of radius 2 cm and density p floats in a transparent liquid of density 2 rho kept in a beaker. The bottom of the beaker is spherical in shape with its radius of curvature 8 cm and is silvered to make it a concave mirror as shown in Fig. When an object is placed a 10 cm directly above the centre of the sphere its final image coincide with it. If 'h' is the height of liquid surface from the apex of the bottom as shown in figure. Consider paraxial rays only for image formation. The refractive index of the sphere is 3/2 and that of the liquid is 4/3 .Answer the following questions. The image formed by the top spherical portion of sphere is (as measured from top of spherical ball)
View Solution
