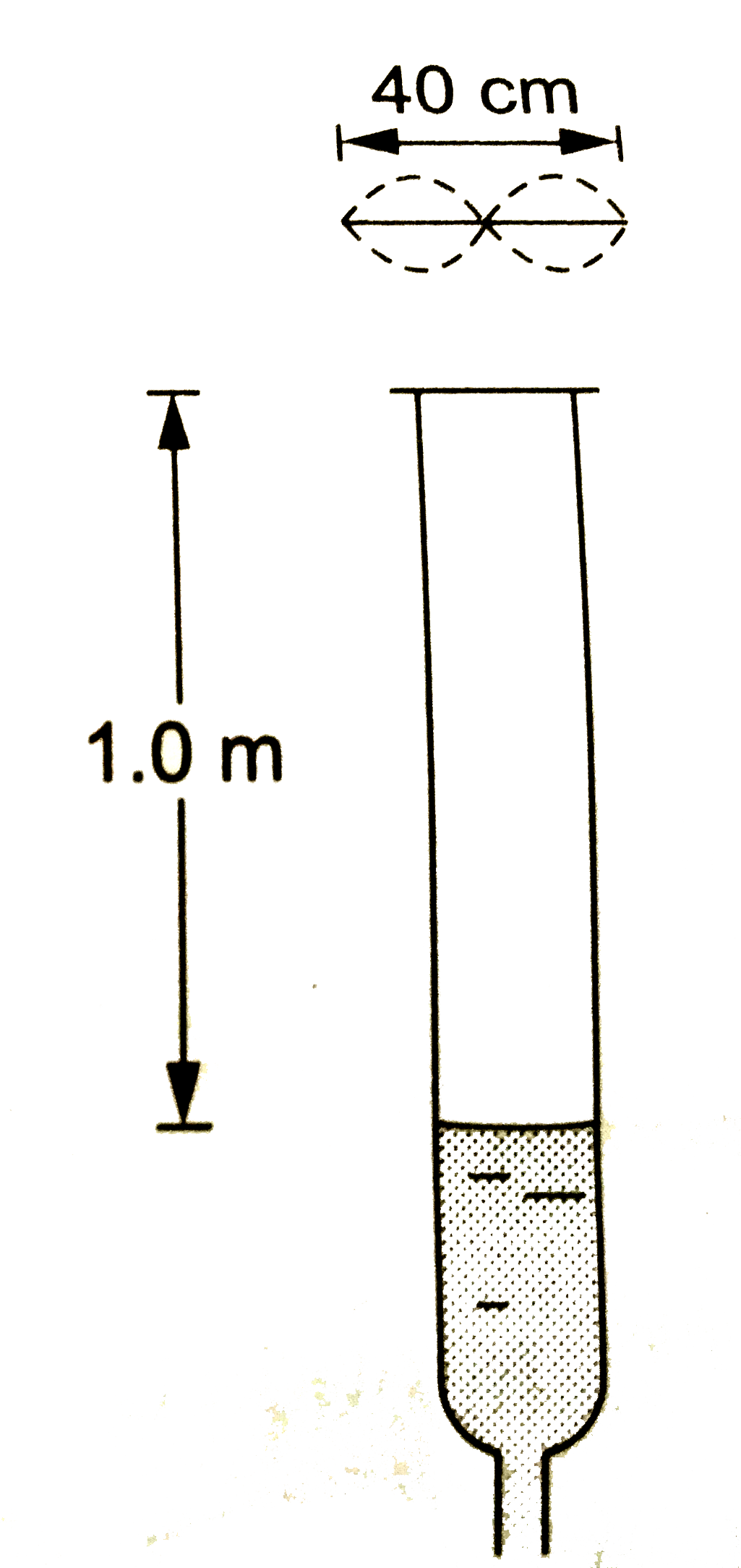
Consider the situation shown in figure. The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 40ms−1, find the tension in the wire.
 .Solution in Tamil
.Solution in Tamil
The correct Answer is:A
Let n0=frequency of the tuning fork,
T=Tension of the string
L=40cm=0.4m,m=4g
=4×10−3kg
So,m=MassUnitLen>h=10−2kgm
n0=12L√Tm
So, 2ndHarmonic2n0=(22L)√Tm
As it is tension with fundamental frequency of vibration in the air column.
→2n0=3404×1=85Hz
→85=22×0.4√T14
=T=(85)2×(0.4)2
=11.6New→n
Topper's Solved these Questions
Similar Questions
A load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
View Solution0.32g of oxygen is kept in a rigid container and is heated. Find the amount of heat needed to raise the temperature from 250C→350C. The molar heat capacity of oxygen at constant volume is 20JK−1mol−1.
View SolutionA 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode.A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air =340ms−1.
View SolutionA tube 1.0 m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3 m long and a mass of 0.01 kg . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find (a) the frequency of oscillation of the air column and (b) the tension in the wire. Speed of sound in air = 330 m//s .
View SolutionA wire of length 40 cm which has a mass of 4 g oscillates in its second harmonic and sets the air column in the tube to vibrations in its funrations in its fundamental mode as shows in figure. Assuming the speed of sound in air as 340 m//s . Find the tension in the wire.
View SolutionA sonometer wire under tension of 128 N vibrates in resonance with a tuning fork . The vibrating portion of sonometer wire has length of 20 cm and mass 1 g . The vibrating wire at constant speed of 0.75 m//s and an observer standing near the sonometer hear 1 beat//s . Find the speed of sound in air.
View SolutionAB wire (length x) is vibrating in its fundamental mode. Wire AB is in resonance with resonance tube in which air column (length x/2) is also vibrating with its fundamental mode. Sound speed is 400 m/sec and linear mass density of AB wire is 10^-4 kg/m and g=10 m//sec^2 , value of mass m = [beta(10^-1)] kg , then find value of beta .Neglect the masses of wires in comparison to block's mass 'm'.
View Solutionएक अनुनाद नली के उप्पर 40 cm लम्बाई तथा 4.00 g द्रिव्यमान का एक तार अपने दोनों किनारो पर स्ठर अवस्था में रखा गया है तार अपने दूसरे सनादि में कंपन कर अनुनाद नली में स्थित 1.0 m लम्बे वयइस्तंब को अपनी मूल विधा (fundamental mode) में अनुनाद कर देता है हवा में धवनि की चाल को 340 m/s मानते हुए तार में तनाव निकाले
View Solutionलम्बाई 30.0 cm तथा द्रिव्यमान 10.0 g का एक तार अपने दोनों किनारो पर स्थित अवस्था में रखा गया है तथा मूल विधा (fundamental mode) में कंपनी कराया जा रहा है 50.0 cm लम्बी एक सिरे पर बंद नली के खुले सिरे को इस तार की पास लाया जाता है कंपन करते तार की कारण नली का वयइस्तंब भी अपनी मूल विधा में कंपन करने लगता है तार में तनाव ज्ञात करे हवा में धवनि की चाल 340 m/s ले
View SolutionA tube 1.0m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3m long and a mass of 0.01kg . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find
(a) the frequency of oscillation of the air column and
(b) the tension in the wire.
Speed of sound in air = 330m/s .
View SolutionThe 1 meter long tube is closed at one end. A drawn wire is placed near the open end. The wire vibrates at its original frequency by 0.3 m and mass is 0.01 kg. Find - (a) Frequency of air column oscillation (b) tension in the wire if the speed of sound in air is 330 m / s
View SolutionA 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode.A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air =340ms−1.
View SolutionA tube 1m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3 m long and has a mass of 0.01 kg. It is held fixed an both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration all its fundamental frequency by resonance Find the tension in the wire. Speed of sound in air: 330 m/s
View SolutionA wire of length 40 cm which has a mass of 4 gms oscillates in its second harmonic and sets the air column in the tube to vibrations in its fundamental mode as shown in figure. Assuming speed of sound in air as 340 m/s, find the tension in the wire.
View SolutionA tube 1.0 m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3 m long and a mass of 0.01 kg . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find (a) the frequency of oscillation of the air column and (b) the tension in the wire. Speed of sound in air = 330 m//s .
View SolutionA wire of length 40 cm which has a mass of 4 g oscillates in its second harmonic and sets the air column in the tube to vibrations in its funrations in its fundamental mode as shows in figure. Assuming the speed of sound in air as 340 m//s . Find the tension in the wire.
View Solution
