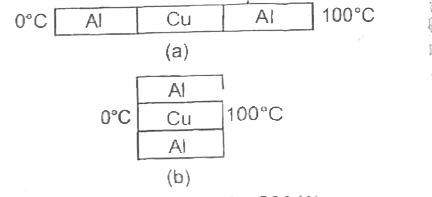
The three rods shown in figure have identica dimensions. Heat flows from the hot end at a rain of 40 W in the arrangement (a). Find the rates of heat flow when the rods are joined as in arrangement (b). (Assume kAJ=200Wm‘∘C and KCu=400Wim‘∘C)
The correct Answer is:D
θ1=θ2=100
QT=Ka(θ1−θ2)t
R=R1+R2+R3 ltbrge =1/(ak_Al)+1/(ak_cu)+1/(ak_Al)<br>=1/a((2/200)+(1/400))<br>1/a((4+1)/400)=1/a 5/400<br>=1/a 1/80<br>Q/t=100/((1/a) (1/80))[:' Q/t=(theta_1-theta_2)/R]<br>40=80xx100xx(a/l)<br>[from question Q/t =40 W.]<br>a/l=1/200<br>for, B R=R1+R2+R3
=RAl+RCuRAlRCu+RAl)
=1aKAl+1aKCu.1aKAl1aKCu.1aKAl
=1aKAl+la(Kal+aKCu)
=1a(1200+1200+400)
=1a(1200+1600)
=1/a((3+1)/(600))=(4/600).(l/a)<br>(Q/t)=(theta_1-theta_2)/R=(100)/((l/4) (4/600))<br>=(600xx100)/4xx(a/l)<br>=(300/4)=75[Using (a/l)=1/200)]<br>For C (1/R)=(1/R_1)+(1/R_1)+(1/R_1)<br>=(1//l)/(ak_(Al))+(1//l)/(ak_(Cu))+(1//l)/(ak_(Al))<br>=(K_(Al)+K_(Cu)+K_(Al)).(a/l)<br>=(2xx200xx400)(a/l)<br>=(a/l)(800)<br>implies R=(a/l)(1/800)<br>(Q/t)=(theta_1-theta_2)/R=(100)/((l/a)(1/800))<br>=(100xx800xxa)/l<br>=(100xx800)/200=400W.



Topper's Solved these Questions
Similar Questions
The three rods shown in figure have identical dimensions. Heat flows from the hot end at a rate of 40 W in the arrangement (a). Find the rates of heat flow when the rods are joined as in arrangement (b). (Assume kAl=200Wm∘C and KCu=400Wm∘C

View Solution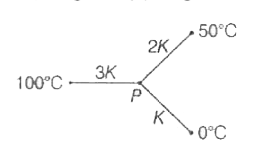
Three rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below
Then , the temperature of the junction in steady - state is
View Solution
Knowledge Check
Two rods of same material and thickness are joined as shown below. The ends X and Y are maintained at X∘C and Y∘C respectively. The ratio of the heat flow in the two rods is –
 A0.36B0.64C10.36D1
A0.36B0.64C10.36D1The three rods described in the previous question are placed individually, with their ends kept at the same temperature difference. The rate of heat flow through C is equal to the rate of combined heat flow through A and B. kc must be equal to
AkA+kBBkAkBkA+kBC12(kA+kB)D2(kAkBkA+kB)
Three rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below

Then , the temperature of the junction in steady - state is
View SolutionAn aluminium rod and copper rod of equal length 1m and cross-sectional area 1cm2 are welded as shown. KA1=200W/m∘C,KCu=400W/m∘C. Find heat current


View SolutionAn aluminium rod and copper rod of equal length 1m and cross-sectional area 1cm2 are welded as shown. KA1=200W/m∘C,KCu=400W/m∘C. Find heat current


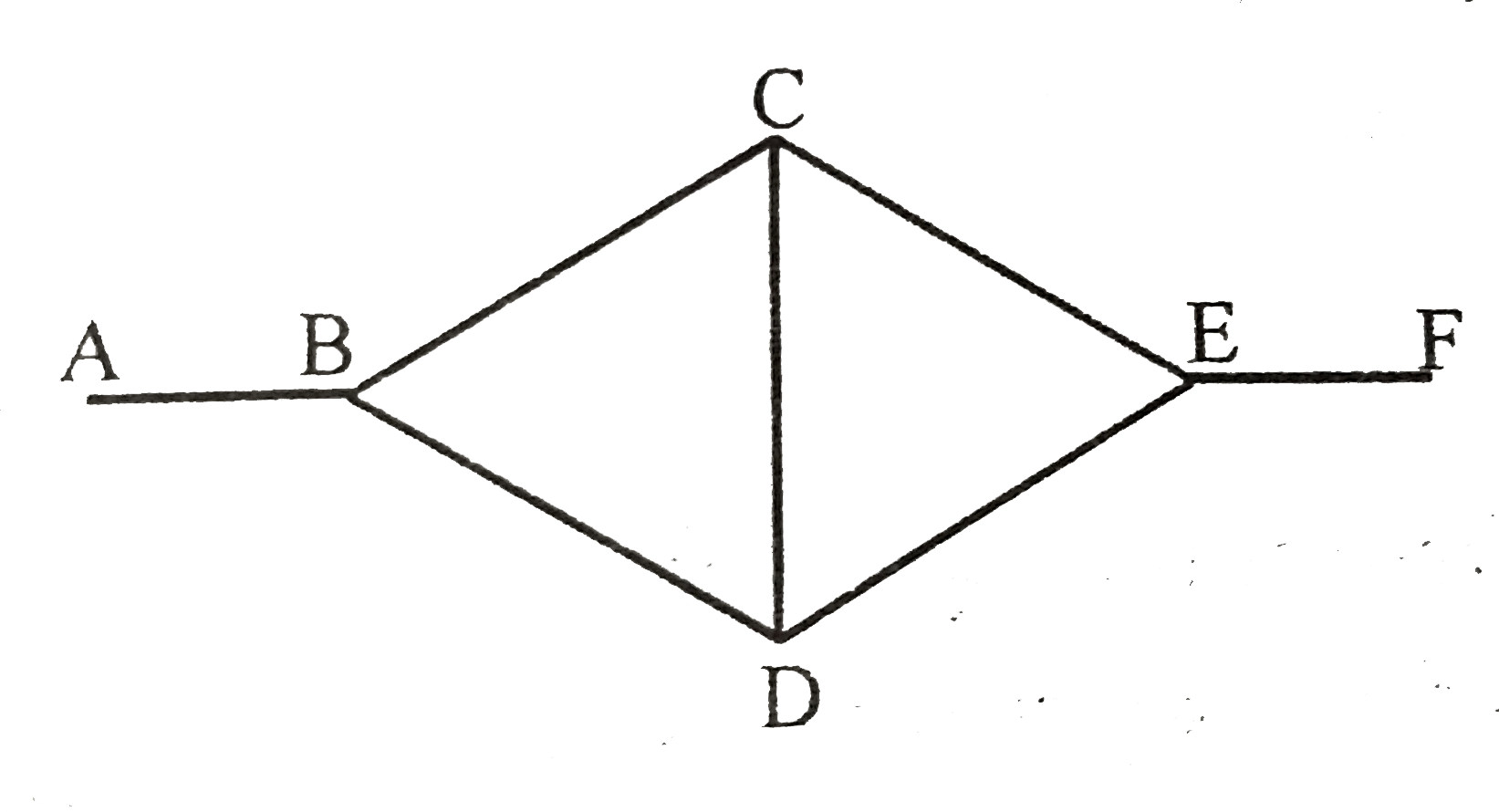
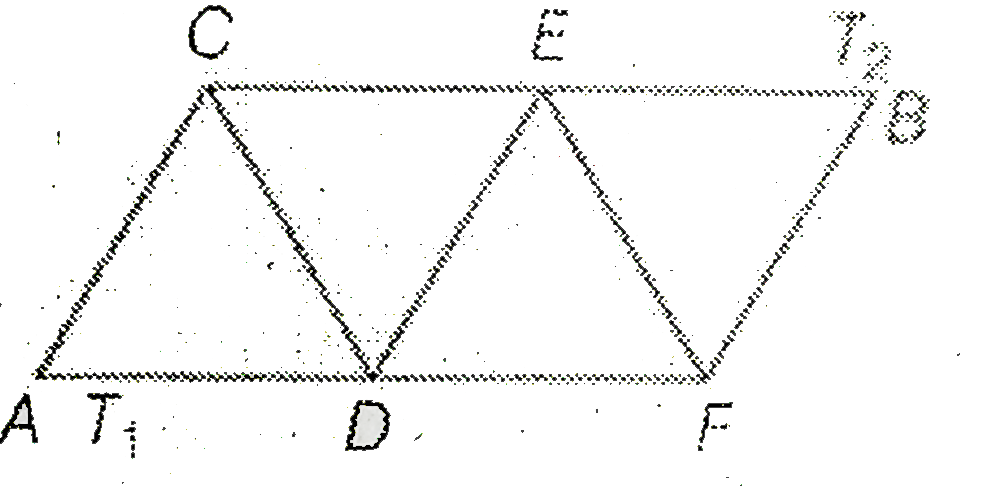
View SolutionIn the frame shown in figure made up of metallic rods of identical size, the ends A and F are maintained at T1 and T2 respectively. The rate of heat flow from A to C is ω. If C and D are instead maintained at T1 & T2 respectively find, find the total rate of heat flow.
View SolutionFind the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1 . Thermal conductivity of the material of the rod is K.

View SolutionNine identical conducting rods are arranged as shown in the figure. The ends A and B are maintained at temperatues T1 and T2. Calculate the ratio of rate of flow of heat across AD to that of EB in the given arrangement in steady state.
View Solution
