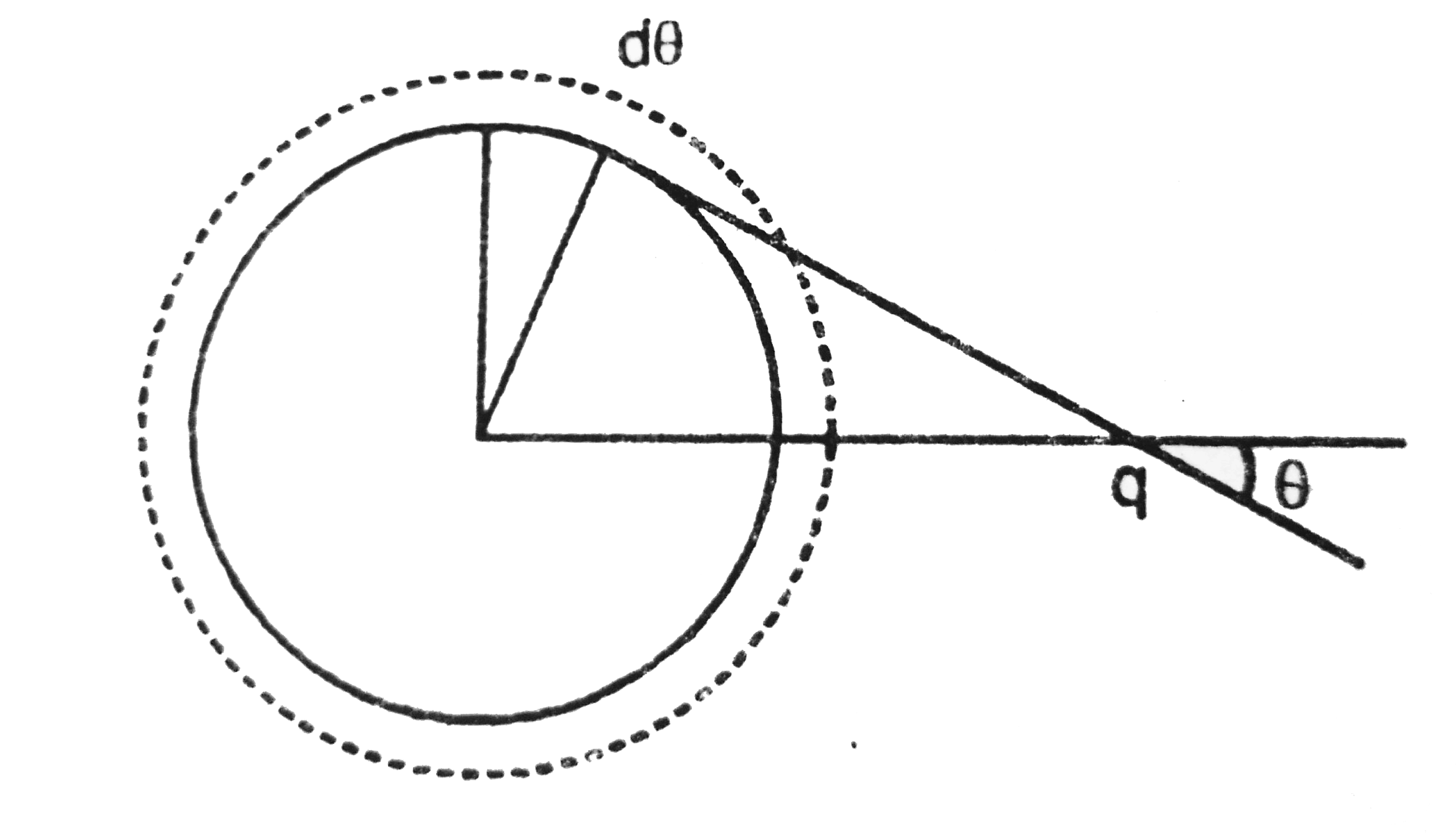
Positive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x is very less than R, find the time period of oscillation of the particle if it is released from there.Solution in Tamil
dq=Q2πR.Rdθ=Q2π.dθ
dE=qdq4πε0(1r2)
=q.Q2πdθ4πε01R2+x2
ordEcosθ=qQdθ8π2ε0x(R2+x2)32
Total force
=∫dFcosθ
=qQ8π2ε0x(R2+x2)32⟨.∫dthη=2π)
x<<R
F=Qqx4πε0R3=mw2x
orm(2πT)2=Qq4πε0R3
T=[16πe3ε0mR3Qq]12.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 28videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercise23videos
ELECTRIC CURRENT THROUGH GASES
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE98videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Mart out the correct options
03:41View SolutionA discharge tube contains helium at a low pressure. A large potential difference is applied across the tube. Consider a helium atom that has just been ionized due to the detachment of an atomic electron. Find the ratio of the distance travelled by the free electron to that by the positive ion in a short time dt after the ionization.
07:15View SolutionCalculate the dimensions of (a) ∫→E.d→l,(b)vBlanddΦ0dt. The symbols have their usual meanings.
05:32View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x ltltR, find the time period of oscillation of the particle if it is released from there.
03:16View SolutionTwo identical coaxial rings each of radius R are separated by a distance of sqrt3R . They are uniformly charged with charges +Q and -Q respectively. The minimum kinetic energy with which a charged particle (charge +q ) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is
04:18View SolutionA thin fixed ring of radius a has a positive chage q unformly distributed over it.A particle of mass m having a megative charge Q, is placed on the axis at a distance of x(xltlta) form the center of the ring. Show that the motion of the negatively chaged particle is approximatly simple harmonic. Calculate the time period of oscillation.
08:00View SolutionA small particle of mass m and charge-q is placed at point P on the axis of uniformly chrarged ring and releases. If R gtgt x , the particle will undergo oscillations along the axis of symmetry with an angurlar frequency that isequal to- .
View SolutionSTATEMENT 1: When a negative charge -q is released at a distance R from the centre and along the axis of a uniformly and positvely charged fixed ring of radius R, the negative charge does oscillation but not SHM. STATEMENT 2: The force on negative charge is always towards the centre of the ring but it is not proportional to the displacement from the centre of the ring.
View SolutionA ring of radius R having total charge Q uniformly distributed over the ring has a charge particle q kept at its centre. If a transverse pulse is created on the ring, then find the time when pulse completes one revolution.(Total mass of ring is m )
View SolutionA thin fixed ring of radius 'R' and positive charge 'Q' is placed in a vertical plane. A particle of mass 'm' and negative charge 'q' is placed at the centre of ring. If the particle is given a small horizontal displacement, show that it executes SHM. Also find the time period of small oscillations of this particle, about the centre of ring. (Ignore gravity)
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
05:11View SolutionA non conducting ring of radius R has uniformly distributed positive chargeq. A small particle of mass m and charge −q is placed on the axis of the ring at point P and released If R>>x. The particle will undergo oscillations along the axis of symmerty with an angular frequency that is equal to
 04:01View Solution
04:01View SolutionA ring of radius R is with a uniformly distributed charge on it. A charge q is now placed at the centre of the ring. Find the increment in tension in the ring.
09:44View SolutionTwo identical coaxial rings each of radius R are separated by a distance of √3R. They are uniformly charged with charges +Q and −Q respectively. The minimum kinetic energy with which a charged particle (charge +q) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is
03:38View SolutionA ring of radius R is carrying uniformly distributed charge +Q . A test charge -q_0 isplaced on its axis at a distance 2R from the centre and released. The motion of the particle on the axis will be :
02:31View SolutionA thin fixed ring of radius a has a positive chage q unformly distributed over it.A particle of mass m having a megative charge Q, is placed on the axis at a distance of x(x<<a) form the center of the ring. Show that the motion of the negatively chaged particle is approximatly simple harmonic. Calculate the time period of oscillation.
 01:54View Solution
01:54View Solution

