Two identical coaxial rings each of radius R are separated by a distance of . They are uniformly charged with charges and respectively. The minimum kinetic energy with which a charged particle (charge ) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is
The correct Answer is:A
To solve the problem, we need to determine the minimum kinetic energy required for a charged particle +q to be projected from the center of the negatively charged ring to reach the center of the positively charged ring.
1. Understanding the Setup:
- We have two identical coaxial rings, each with radius R.
- The distance between the two rings is √3R.
- The first ring (let's call it Ring A) has a charge of −Q and the second ring (Ring B) has a charge of +Q.
2. Identifying the Forces:
- When the charged particle +q is projected from the center of Ring A, it will experience an attractive force due to the negatively charged ring and a repulsive force from the positively charged ring as it approaches.
3. Using Conservation of Energy:
- The total mechanical energy at the starting point (center of Ring A) must equal the total mechanical energy at the final point (center of Ring B).
- The equation can be expressed as:
KA+UA=KB+UB
- Here, KA is the initial kinetic energy, UA is the potential energy at the center of Ring A, KB is the kinetic energy at the center of Ring B (which we want to be zero for minimum energy), and UB is the potential energy at the center of Ring B.
4. Calculating Potential Energies:
- The potential energy UA at the center of Ring A (due to Ring B) is given by:
UA=−kQq√R2+(√3R)2=−kQq2R
- The potential energy UB at the center of Ring B (due to Ring A) is given by:
UB=kQq√R2+(√3R)2=kQq2R
5. Setting Up the Energy Equation:
- Since we want KB=0 for minimum kinetic energy, we can substitute:
KA−kQq2R=0+kQq2R
- Rearranging gives:
KA=kQqR
6. Final Result:
- Thus, the minimum kinetic energy with which the charged particle +q should be projected from the center of the negatively charged ring is:
K=kQqR
- We have two identical coaxial rings, each with radius R.
- The distance between the two rings is √3R.
- The first ring (let's call it Ring A) has a charge of −Q and the second ring (Ring B) has a charge of +Q.
- When the charged particle +q is projected from the center of Ring A, it will experience an attractive force due to the negatively charged ring and a repulsive force from the positively charged ring as it approaches.
- The total mechanical energy at the starting point (center of Ring A) must equal the total mechanical energy at the final point (center of Ring B).
- The equation can be expressed as:
KA+UA=KB+UB
- Here, KA is the initial kinetic energy, UA is the potential energy at the center of Ring A, KB is the kinetic energy at the center of Ring B (which we want to be zero for minimum energy), and UB is the potential energy at the center of Ring B.
- The potential energy UA at the center of Ring A (due to Ring B) is given by:
UA=−kQq√R2+(√3R)2=−kQq2R
- The potential energy UB at the center of Ring B (due to Ring A) is given by:
UB=kQq√R2+(√3R)2=kQq2R
- Since we want KB=0 for minimum kinetic energy, we can substitute:
KA−kQq2R=0+kQq2R
- Rearranging gives:
KA=kQqR
- Thus, the minimum kinetic energy with which the charged particle +q should be projected from the center of the negatively charged ring is:
K=kQqR
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.14videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.29videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
The minimum velocity v with which charge q should be projected so that it manages to reach the centre of the ring starting from the position shown in figure is
 View Solution
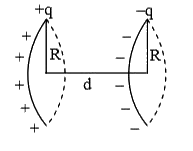
View SolutionTwo thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -
 View Solution
View SolutionA ring of radius R has charge −Q distributed uniformly over it. Calculate the charge that should be placed at the center of the ring such that the electric field becomes zero at apoint on the axis of the ring at distant R from the center of the ring.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .
 View Solution
View SolutionTwo concentric rings placed in a gravity free region in yz-plane one of radius R carries a+Q and second of radius 4R and charge –8Q distributed uniformly over it. Find the velocity with which a point charge of mass m and charge +q should be projected from a a distance 3R from the centre of rings on its axis so that it will reach to the centre of the rings.
View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionTwo identical rings PandQ of radius 0.1m are mounted coaxially at a distance 0.5m apart. The charges on the two rings are 2μCand4μC, respectively. The work done in transferring a charge of 5μC from the center of P to that of Q is.
View SolutionA Circular ring of radius 3a is uniformly charged with charge q is kept in x−y plane with center at origin. A particle of charge q and mass m is projected frim x=4 towards origin. Find the minimum speed of projection such that it reaches origin.
_2019_CBT5_E01_042_Q01.png) View Solution
View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionA thin circular wire of radius r has a charge Q. If a point charge q is placed at the centre of the ring, then find the increase in tension in the wire.
View Solution

