Shows a conducting circular loop radius a placed in a uniform, perpendicular magnetic field B. A metal rod OA is pivoted at the centre O of the loop. The other A of the rod touches the loop. The rod OA and the loop are resistanceless but a resistor having a resistance R is connected between O and a fixed point C on the loop . the rod OA is made to rotate anticlockwise at a small but uniform angular speed omega by an external force. Find (a) the current in the resistance R and (b) the torque of the external force needed ot keep the rod rotating with the constant angular velocity omega.
 Solution in Tamil
Solution in Tamil
The emf between the ends of the rotating rod is ε=∫dε=∫a0Bωxdx=12Bωa2
The positive charges of the rod will be pushed towards O by the magnetic field
Thus, the rod may be replaced by a battery of emf=12Bωa2 with the positive terminal towards O
The equivalent circuit diagram is shown in the circular loop joins A to C by a resistanceless path
(a) The current in the resistance R is i=εR=Bωa22R
(b) the force on the rod due to the magnetic field is F=iaB
As the force is uniformly distributed over OA, it may be assumed to act at the middle point of OA
The torque is, therefore, Γ=(iaB)a2=B2ωa44R in clockwise direction
To keep the rod rotating at uniform angular velocity, an external torque B2ωa44R in anticlockwise direction is needed.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer10videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 112videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE98videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise9videos
ELECTROMAGNETIC WAVES
Similar Questions
A short magnet is moved along the axis of a conducting loop. Show that the loop repels the magnet if the magnet is approaching the loop and attracts the magnet if it is going away from the loop.
10:27View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
02:54View SolutionCalculate the dimensions of (a) ∫→E.d→l,(b)vBlanddΦ0dt. The symbols have their usual meanings.
00:57View SolutionFind the dimensional formula of ε0 .
10:37View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
02:13View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v_0 , parallel to an infinite conducting wire carrying current i_0 . A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v_0/2 along the direction 2 of the current. At the instant t = 0 , the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop. (a) The current through the rod when it is at a distance of (a/2) from the point A of the loop. (b) Force required to maintain the velocity of the rod at that instant.
View SolutionFig. Shows a conducting circular loop of radius a placed in a uniform, perpendicular magnetic field B. A thick metal rod OA is pivoted at the centre O. The other end of the rod touches the loop at A. The centre O and a fixed point C on the loop are connected by a wire OC of resistance R. A force is applied at the middle point of the rod OA perpendicularly, so that the rod rotates clockwise at a uniform angular velocity (ω). Find the force.
 04:03View Solution
04:03View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
05:05View SolutionFigure shows a conducting circular loop of radius a placed in a uniform, perpendicular magnetic field B.A thick metal rod OA is pivoted at the centre O . The other end of the rod toucher the loop are connected by a wire OC of resistance R.A force is applied at the middle point of the rod OA perpendicularly, so that the rod rotates clockwise at a uniform angular velocity ω . Find the force.
(b) Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its lenght. The rod OA is made to rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when ∠AOC=90∘ .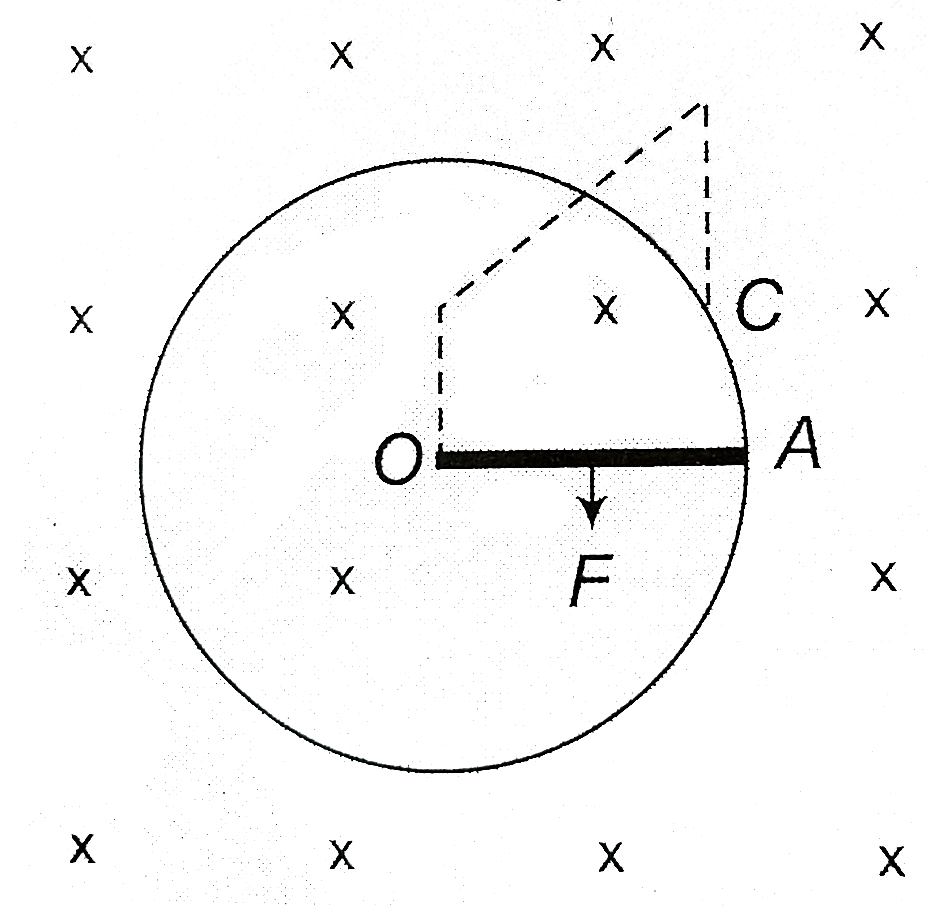 04:50View Solution
04:50View SolutionA horizontal conducting loop of radius R is fixed in air. A uniformly charged rod having charge Q on it is held vertically above the conducting loop at a height h above it. The rod is released and it begins to fall along the axis of the loop. Calculate the emf induced in the conducting loop.
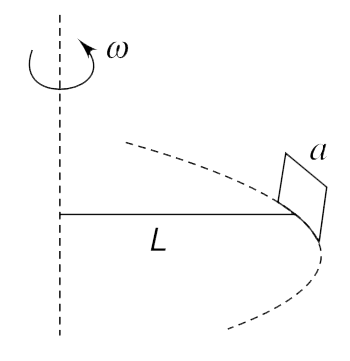
01:33View SolutionA conducting square loop of side length a is held vertical with the help of a non conducting rod of length L. The rod is made to rotate in horizontal circle about a vertical axis through its end. The loop rotates with the rod while its plane always remains perpendicular to the rod. The resistance of the loop is R and angu- lar speed of the rod is ω. There is a uniform horizontal magnetic field B in the entire space. Find the average rate of heat dissipation in the loop during one rotation.
 01:07View Solution
01:07View SolutionA conducting circular loop of radius r carries a constant current I. It is placed in a uniform magnetic field vec(B) such that vec(B) is perpendicular to the plane of the loop. The magnetic force acting on the loop is
04:04View Solutionएक बेलनाकार छड़ चुम्बक को किसी वृत्तीय चालक लूप के अक्ष पर पकड़कर रखा गया है। निम्नलिखित में से छड़ चुम्बक के किस संचलन से लूप में प्रेरित धारा उत्पन्न नहीं होगी।
13:27View SolutionA circular loop of metal wire of radius r is placed perpendicular to uniform magnetic field B. Half of the loop is folded about the diameter with constant angular velocity omega . If resistance of the loop is R then current in the loop is
02:15View SolutionA conducting circular loop of radius r carries a constant current i.It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
View Solution

