Shows a situation similar to the previous problem. All parameters are the same except that a battery of emf and a variable resistance R are connected wires. Let be the angle made by the rod from the horizontal position (shown in the figurer), measuredin the clockwise direction. During the part of the motion the only forces acting on the rod are gravity and the forces exerted by the magnetic field and the pivot. However, during the part of the motion, the resistance R is varied in such a way that the rod continues to rotate with a constant angular velocity . Find the value of R in terms of the given quantities.
 Solution in Tamil
Solution in Tamil
E.m.f=(B omega a^2)/2 [from previous problem]
.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
9 Videos
Similar Questions
A bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
View SolutionFind the dimensional formula of ε0 .
View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
View SolutionConsider a situation similar ot that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) what force is needed ot keep the rod sliding at a constant speed v? (b) in this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) find the power delivered by the external agent exerting the force on the rod.
View SolutionConsider a variation of the previous problem. Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistances but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity ω in the clockwise direction by applying a force at the midpoint of OA in a dirction perpendicular ot it. find the magnitude of this force when the rod makes an angle θ with the vertical.
View SolutionConsider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed (ω) as shown in the figure. Find the current in the rod when −AOC=90∘
View SolutionConsider a variation of the previous problem. Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistance but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity (ω) in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it.
Find the magnitude of this force when the rod makes an angle (θ) with the vertical.
View SolutionFigure shows a situation similar to the previous problem. All parameters are the same except that a battery of emf ε and a variable resistance R are connected between O and C. The connecting wires have zero resistance. No external force is applied on the rod (except gravity, forces by the magnetic field and by the pivot).

In what way should the resistance R be changed so that the rod may rotate with uniform angular velocity in the clockwise direction? Express your answer in terms of the given quantities and the angle (θ) made by the rod OA with the horizontal.
View SolutionA uniform rod of mass M and length L is hinged at its end to a wall so that it can rotate freely in a horizontal plane. When the rod is perpendicular to the wall a constant force F starts acting at the centre of the rod in a horizontal direction perpendicular to the rod. The force remains parallel to its original direction and acts at the centre of the rod as the rod rotates. (Neglect gravity). (a) With what angular speed will the rod hit the wall ? (b) At what angle theta (see figure) the hinge force will make a 45^(@) angle with the rod ?
View SolutionDetermine the point of application of force, when forces are acting on the rod as shown in figure.
View SolutionDetermine the point of application of force, when forces are acting on the rod as shown in figure.[here 10N force make 37° with horizontal]
View SolutionConsider a situation similar ot that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) what force is needed ot keep the rod sliding at a constant speed v? (b) in this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) find the power delivered by the external agent exerting the force on the rod.
View SolutionConsider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when <AOC=90∘.
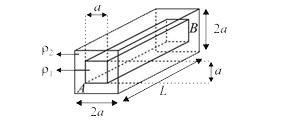
View SolutionA composite rod made up of two conductors of resistivity ρ1 and ρ2 is shown in the figure. If face A and B are connected to a battery, find the resistance of the rod.
View SolutionA battery of emf epsilon and internal resistance r is connected across a load resistance R_L . The plot between output power and load resistance is shown in the figure The value of emf epsilon and internal resistance r respectively will be
View SolutionConsider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed (ω) as shown in the figure. Find the current in the rod when −AOC=90∘
View Solution
