Consider a situation similar ot that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) what force is needed ot keep the rod sliding at a constant speed v? (b) in this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) find the power delivered by the external agent exerting the force on the rod.
(a) e.m.f produced due to the current carrying wire<br> =(mu_0 iv)/(2 pi)In((2x+1)/(2x-1))<br>Let current produced in the rod = I'=(mu_0iv)/(2 pi R)In((2x+1)/(2x-1))<br>force on the wire considering a small portion dx at a distance x.<br>dF=I'Bl<br>implies dF=(mu_0 iv)/(2 pi R)In((2x+l)/(2x-l))xx(mu_0iv)/(2 pi x)xxdx<br> dF=((mu_0i)/(2 pi ))^2 (v/R) In ((2x+l)/(2x-l))(dx)/(x)<br> F=((mu_0i)/(2 pi ))^2 (v/R) In ((2x+l)/(2x-l)) int_(x+(l/2))^(x-(l/2)) dx/x<br>=((mu_0i)/(2 pi ))^2 (v/R) In ((2x+l)/(2x-l))In ((2x+l)/(2x-l))<br>=(vR[μ0i2πIn(2x+l2x−l)]2
(b)Current,i'=μ0iv2πRIn(2x+l2x−l)
(c)Rateofheatdeveloped,w=i2R
μ0iv2πR(2x+l2×xl)]2R
=(1R)[μ0iv2πIn(2x+l2x−l)]2
(d)Powerdeveloped∈rateofheatdeveloped=i2R
=(1R)[μ0iv2πIn(2x+l2x−l)]2.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
In the previous problem, the rod on which the ring slide is vertical Repeat the problem.
View SolutionConsider the situation of the previous problem. (a) Calculate the force needed to keep the sliding wire moving with a constant velocity v. (b) If the force needed just after t = 0 is F0, find the time at which the force needed will be F0 /2.
View Solution
Knowledge Check
Figure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
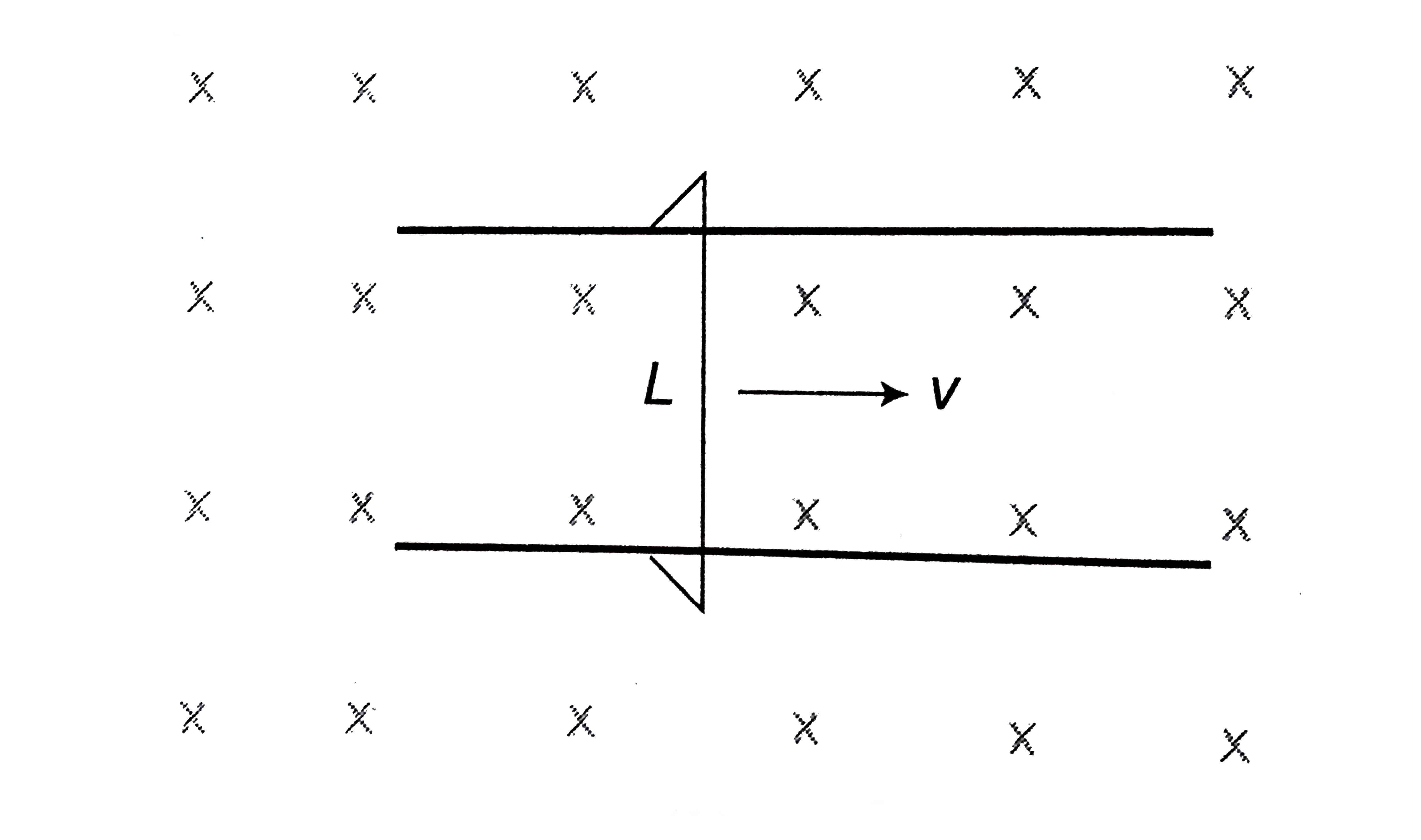 ABvLBBv2LCzeroDB2v2L/R
ABvLBBv2LCzeroDB2v2L/RFigure shows a situation similar to the previous problem. All parameters are the same except that a battery of emf ε and a variable resistance R are connected between O and C. The connecting wires have zero resistance. No external force is applied on the rod (except gravity, forces by the magnetic field and by the pivot).

In what way should the resistance R be changed so that the rod may rotate with uniform angular velocity in the clockwise direction? Express your answer in terms of the given quantities and the angle (θ) made by the rod OA with the horizontal.A(Bωa2−2ε)aB2mgcosθB(Bωa2+2ε)aBmgcosθC(Bωa2+2ε)aB2mgcosθDNone of theseA wire having mass m and length 1 can freely slide on a pair or parallel smooth horizontal rails placed in vertical magnetic field B. The rails are connected by a capacitor of capacitance C . The electric resistance of the rails and the wire is zero .If a constant force F acts on the Wire as shown in the figure . Then ,the acceleration of the wire can be given as
 Aa=C2B2l−FmBa=Fm+CBlCa=FC2B2lmDa=Fm+C2B2l
Aa=C2B2l−FmBa=Fm+CBlCa=FC2B2lmDa=Fm+C2B2l
Figure shows a wire ab of length l which can slide on a U-shaped rail of negligible resistance. The resistance of the wire is R. The wire is pulled to the right with a constant speed v. Draw an equivalent circuit diagram representing the induced emf by a battery. Find the current in the wire.
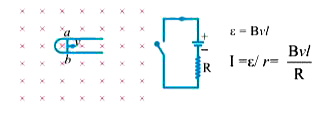
View SolutionWhat will be the motion of the conductor of the previous problem, if a resistor of resistance R is connected into the circuit instead of the capacitor? Neglect the resistance of the conductors.
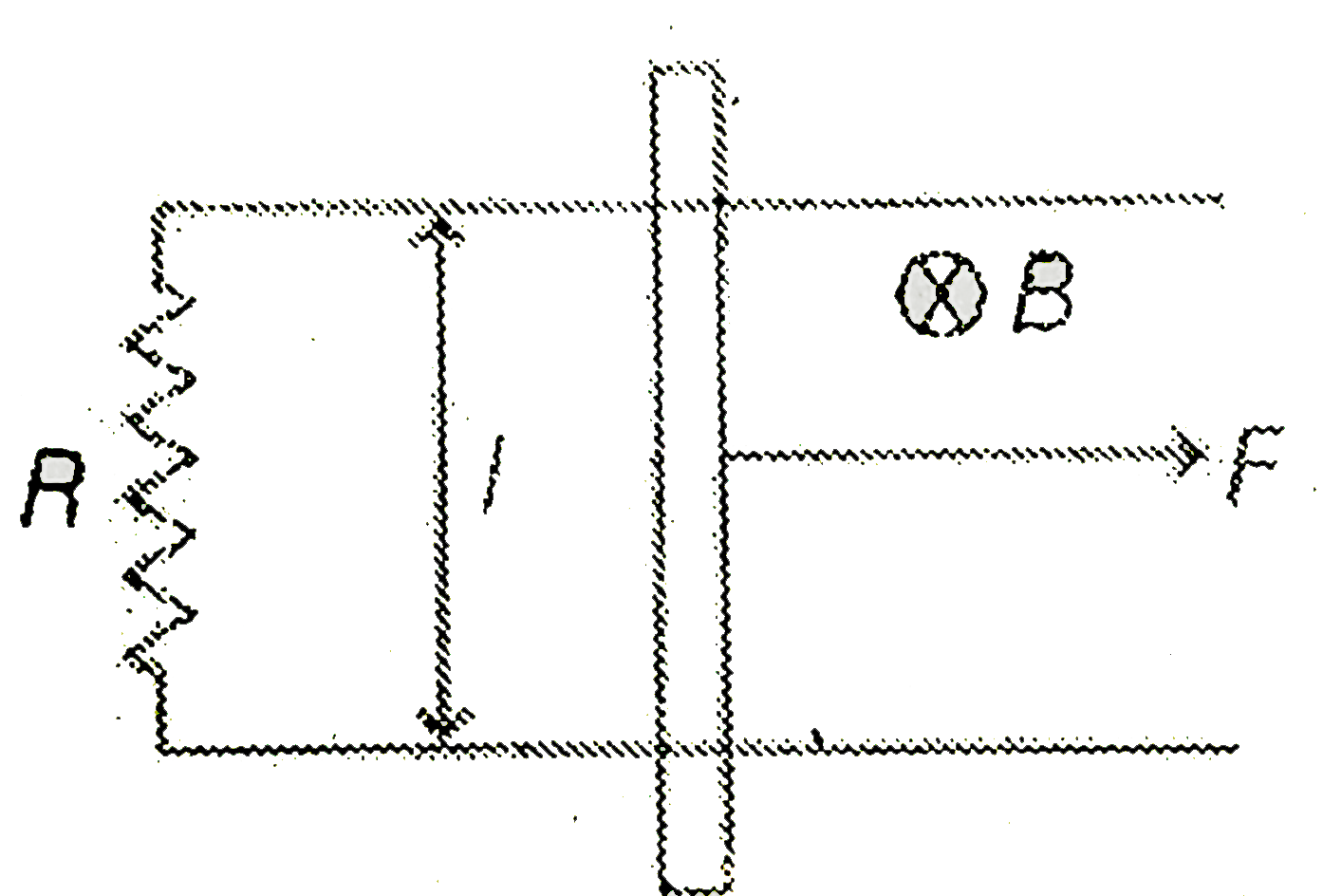
View SolutionA constant force is being applied on a road of length 'l' kept at rest on two parallel conducting rails connected at ends by resistance R in uniform magnitic field B shown.
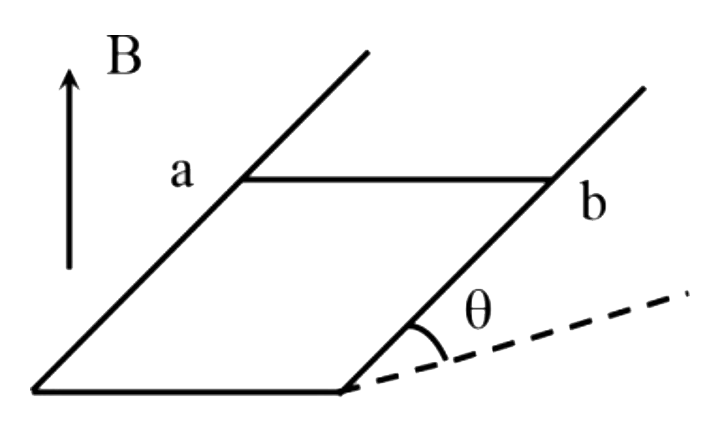
View SolutionA wire ab of length l, mass m and resistance R slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle θ with the horizontal. A vertical magnetic field B exist in the region. If the wire slides on the rails at a constant speed v, then the value of B is -
View SolutionConsider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed (ω) as shown in the figure. Find the current in the rod when −AOC=90∘
View Solution
