Wheatstone's bridge is a very simple but powerfull concept which has made many calculations easy. If the assumption is made that current does not flow through the galvanometer from B to C or C to B,
VA−VB=VA−VD VB−VD=VC−VD
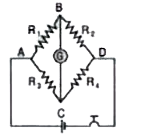
The current in R1, has to flow through BD and that in R3 through CD. This idea has been extended to many symmetrical circuits.
For Wheatstone's bridge,
it is necessary that R1=R2 and R3=R4
it is necessary that the current in R1 should be equal to current in R3
it is not necessary that the current in R1 should be equal to the current in R3.
the current in R2 should be the same that in R4
The correct Answer is:C
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - MULTIPLE CHOICE QUESTIONS ( LEVEL-II)
54 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - MULTIPLE CHOICE QUESTIONS (PARAGRAPH QUESTIONS)
2 Videos
- ATOMS, MOLECULES AND NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEIEXERCISE - Recent Competitive Questions
40 Videos
- DESCRIPTION OF MOTION IN ONE DIMENSION BOOK - MODERN PUBLICATIONCHAPTER - DESCRIPTION OF MOTION IN ONE DIMENSION EXERCISE - Revision Test
45 Videos
Similar Questions
Knowledge Check
Assertion (A): In balanced condition of a Wheatstone bridge, there is no current flow through the galvanometer.
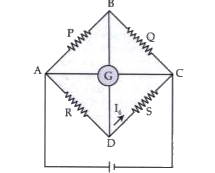
Reason (R ): The potential of point B and D are same.ABoth A and R are true and R is the correct explanation of ABBoth A and R are true but R is NOT the correct explanation of ACA is true but R is falseDA is false and R is trueFind the value of R for which no current will flow through 5V battery
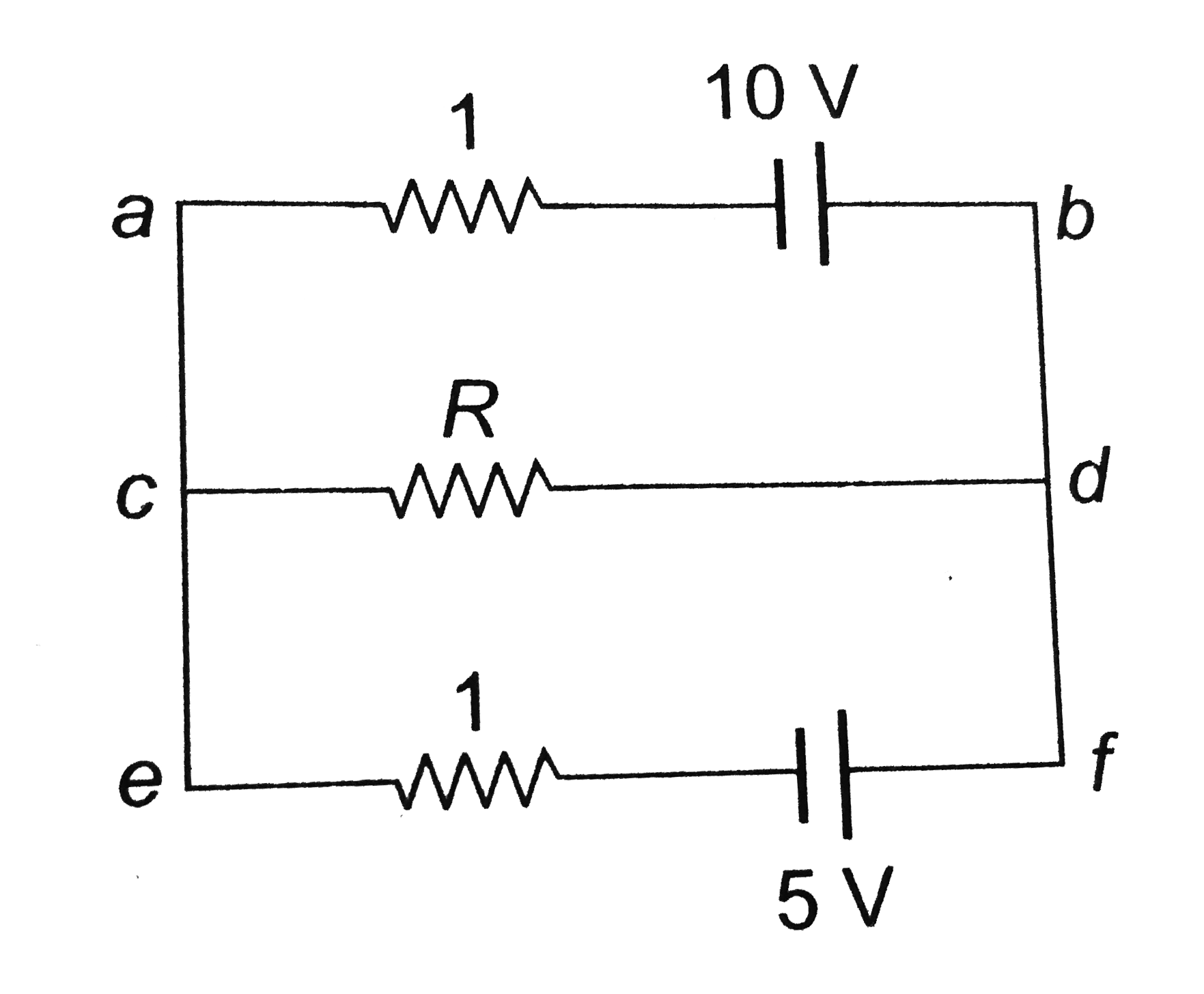 A4ΩB1ΩC3ΩD4Ω
A4ΩB1ΩC3ΩD4ΩThe p.d (VB−VC between two point from C to B
Adoes not depend on the pathBdepends on the pathCdepends on test chargeDindependent of electric field
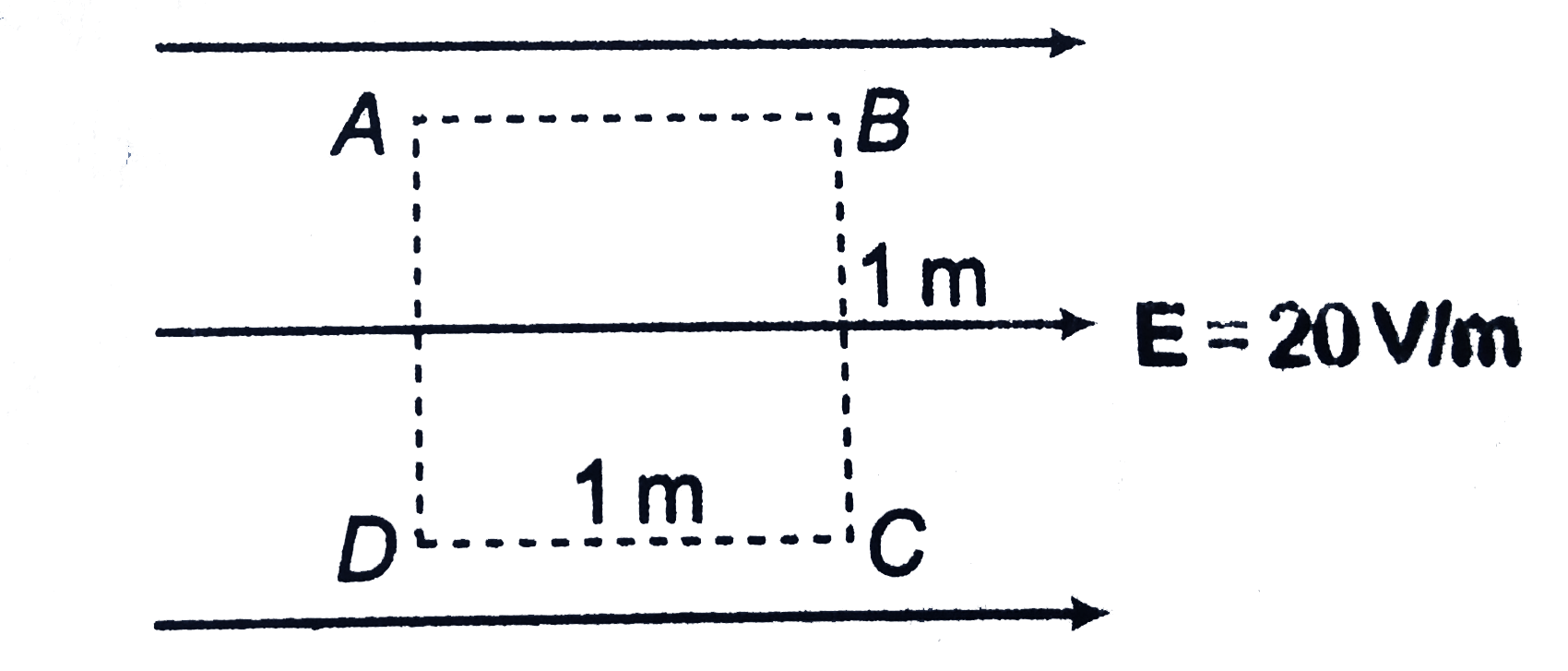
In the uniform electric field shown in figure, find :
a. VA−VD
b. VA−VC
c. VB−VD
d. VC−VD
View SolutionIf the above question, the potential has correct relations as given=
A. VA>VB>VC>VD
B. VA>VB≥VC>VD
C. VD=VC=VB=VA
D. VC<VB>VA>VD
View SolutionFind out following

(i) VA−VB (ii) VB−VC (iii) VC−VA (iv) VD−VC
(v) VA−VD (vi) Arrange the order of potential for points A, B, C and D.
View SolutionFind out following

(i) VA−VB (ii) VB−VC (iii) VC−VA (iv) VD−VC
(v) VA−VD (vi) Arrange the order of potential for points A, B, C and D.
View SolutionIn the circuit shown in the figure , no current flows through the 8 Ω resistor, then the potential difference between points A and B(VA−VB)is
_PHY_E01_001_Q01.png)
View Solution
