A closed triangular box is kept in an electric field of magnitude $E = 2 \times 10^{3} N C^{- 1}$ as shown in the figure.

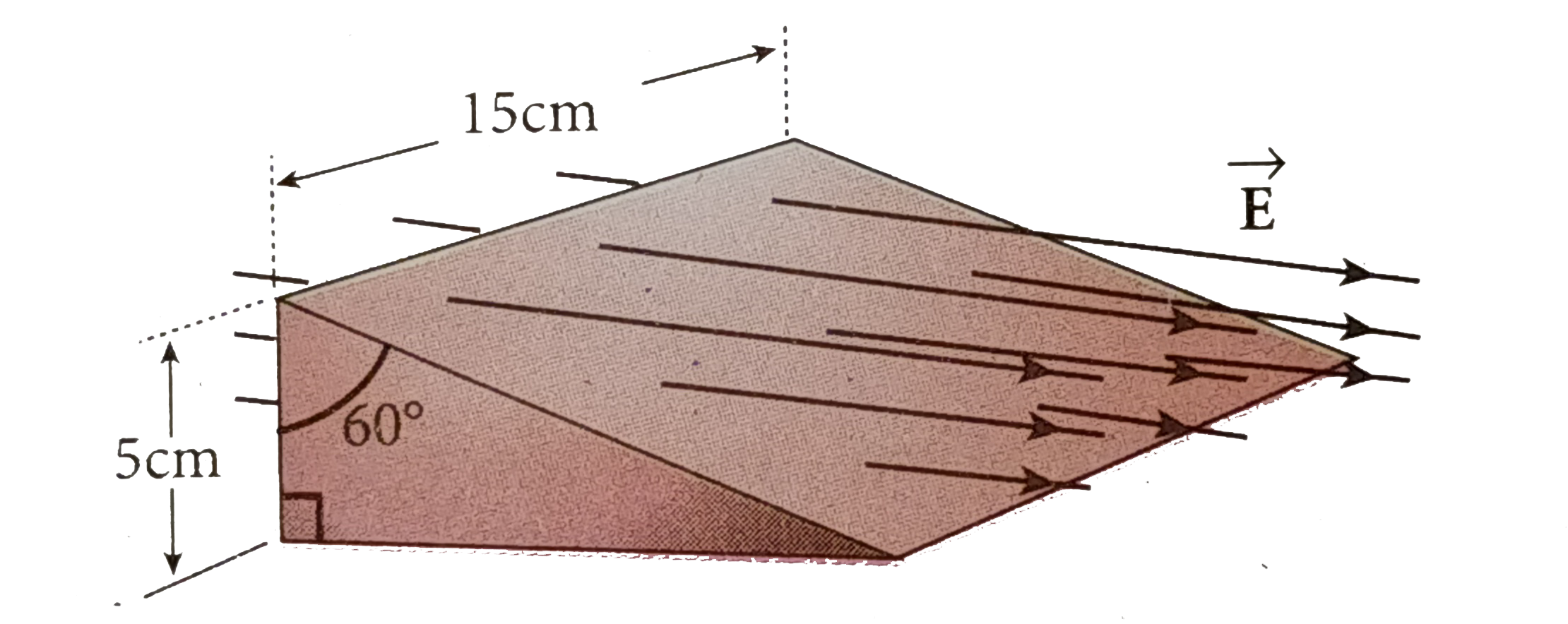
Calculate the electric flux through the vertical rectangular surface

Text Solution

Verified by Experts

The correct Answer is:The magnitude of electric field $E = 2 \times 10^{3} N C^{- 1}$ Area of the surface $A = 0.15 \times 0.05$
[From the diagram 1=15 cm =0.15 m, b=5 cm =0.05m]
The electric flux through
To find:

Vertical rectangular surface $ϕ_{vert} = ?$
According to Gauss law $ϕ = E A cos θ$
$ϕ_{vertical surface} = 2 \times 10^{3} \times 0.15 \times 0.05 \times {cos θ}^{\circ}$
$= 0.015 \times 103$
$= 15 N m^{2} C^{- 1}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Similar Questions

Knowledge Check

Question 1 - Select One
A circular plane sheet of radius 10 cm is placed in a uniform electric field of $5 \times 10^{5} N C^{- 1}$ , making an angle of $60^{\circ}$ with the field. Calculate electric flux through the sheet.
A $1.36 \times 10^{2} N m^{2} C^{- 1}$
B $1.36 \times 10^{4} N m^{2} C^{- 1}$
C $0.515 \times 10^{2} N m^{2} C^{- 1}$
D $0.515 \times 10^{4} N m^{2} C^{- 1}$
Question 2 - Select One
An electron falls through a small distance in a uniform electric field of magnitude $2 \times 10^{4} N C^{- 1}$ . The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
ASame in both cases
BMore in the case of electron
CMore in the case of proton
DIndependent of charge

Recommended Questions

Home
Ask Doubt
Profile