Capacitors P and Q have identical cross sectional areas A and separation d. The space between the capacitors is filled with a dielectric of dielectirc constant εe as shown in the figure. Calcualate the capacitance of capacitors P and Q. 
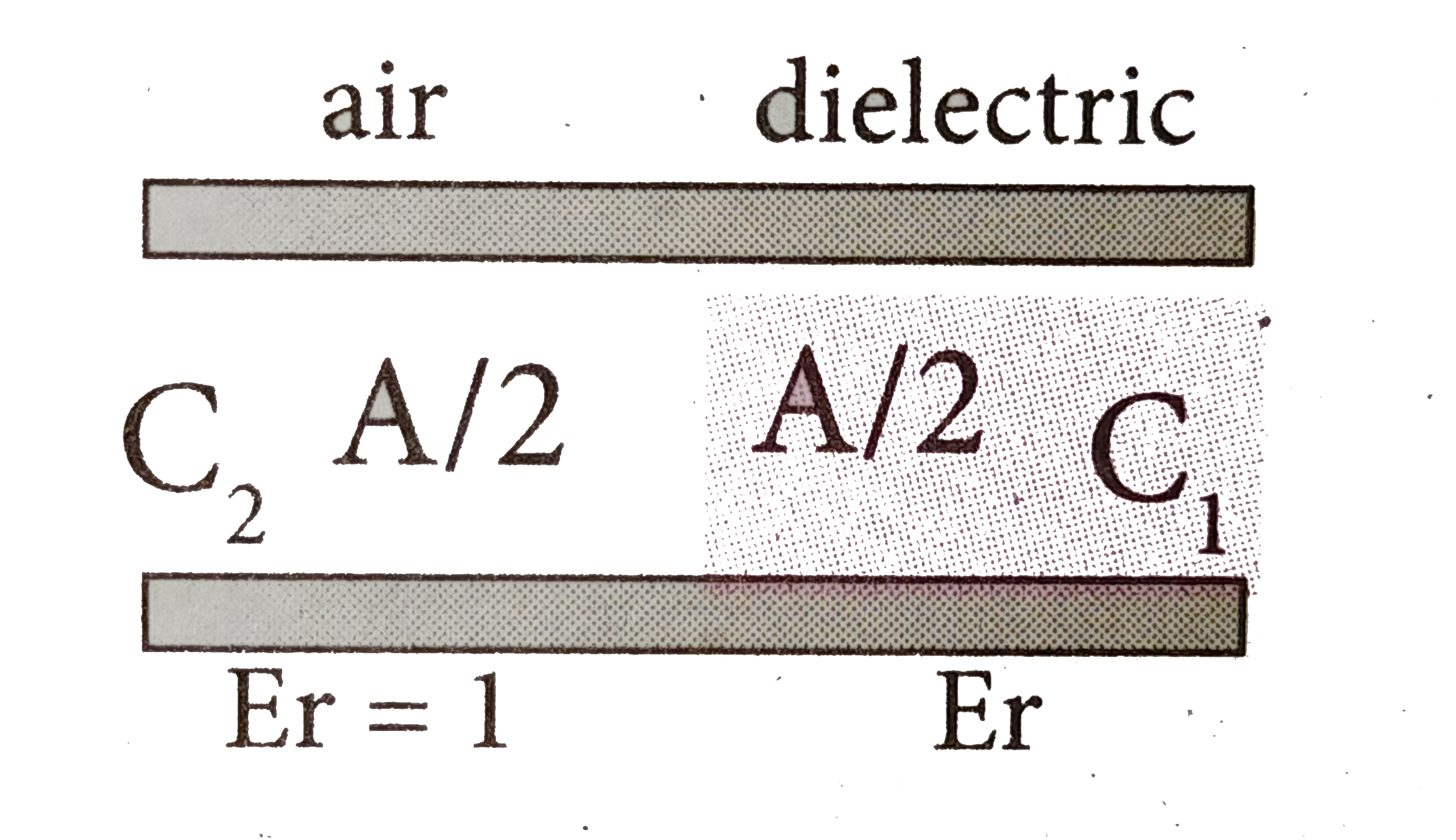
The given arrangement is equivalent to parallel combination of the capacitor each plate of ares =A2
Plate of separation =d
The medium of one dielectirc constant =K1,
εr=1(air)K1=1
The medium of other dielectric constant =K2,i.e.K2=ε0
The capacitance of K1=C1
The capacitance for K2=C2 [C=εAd]
C1=ε0A2.K1d=ε0K1A2d
C2=ε0A2.K1d=ε0K1A2d
If C is the capacitance of the capacitor. then C=C1+C2
=ε0K12d+ε0K2A2d=ε0(K1+K2)A2d
C=ε0(1+εr)A2d
For capacitor Q.

This is equivalent to a series combination of two capacitors
Plate of separation d2
Dielectric constant for first medium =K1 [dielectric K1=εr]
Capacitance of first C1=ε0K1Ad2=2ε0K1Ad
For second Capacitance C2=ε0K2Ad2=2ε0K2Ad
If C is the capacitance of the capacitor
1C=1C1+1C2
=d2ε0A[1K1+1K2]=d2ε0A.[K1+K2K1K2]
1C=d2ε0A[1+εrεr]
C=2ε0Ad[εr1+εr]
Similar Questions
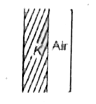
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
View SolutionA parallel plate capacitor of capacitance C (without dielectric) is filled by dielectric slabs as shown in figure. Then the new capacitance of the capacitor is
View Solution
Knowledge Check
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
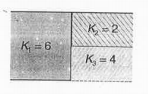
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]In the figure a capacitor id filled with dielectric. The resultant capacitance is
 A2ε0Ad[1k1+1k2+1k3]Bε0Ad[1k1+1k2+1k3]C2ε0Ad[k1+k2+k3]DNone of these
A2ε0Ad[1k1+1k2+1k3]Bε0Ad[1k1+1k2+1k3]C2ε0Ad[k1+k2+k3]DNone of these
The capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
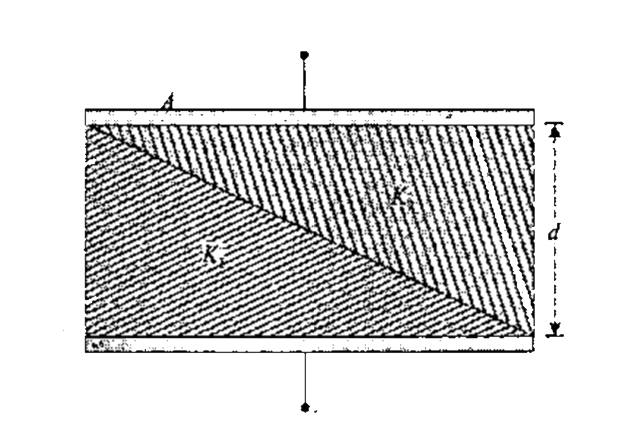
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

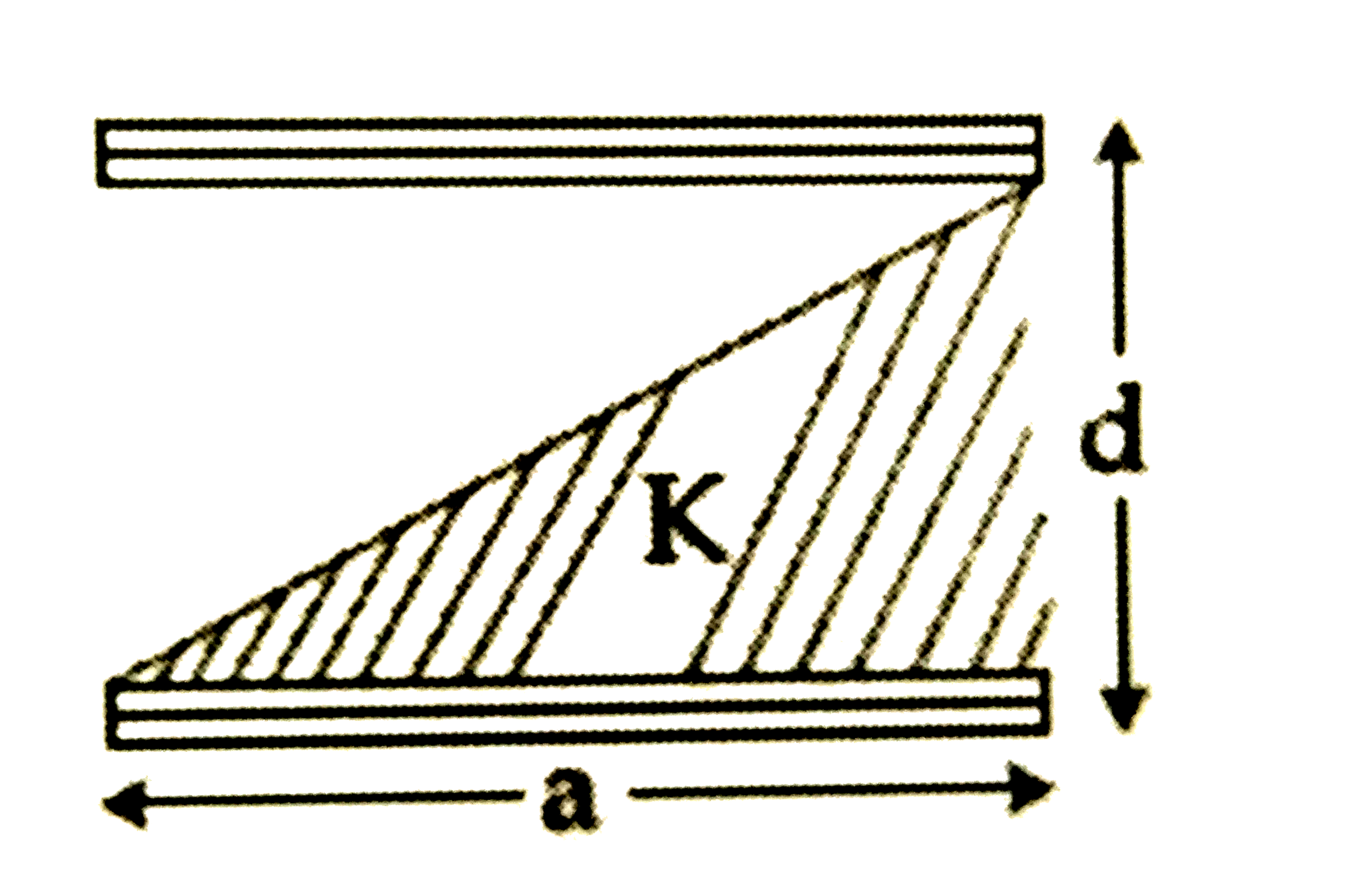
View SolutionA paralled plate capacitor is made of two square plates of side 'a' , separated by a distance d (dltlta). The lower triangular portion is filled with a dielecttic of dielectric constant K, as shown in the figure. Capacitance of this Capacitor is :
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionFour capacitors are connected as shown in the figure. The equivalent capacitance between P and Q is
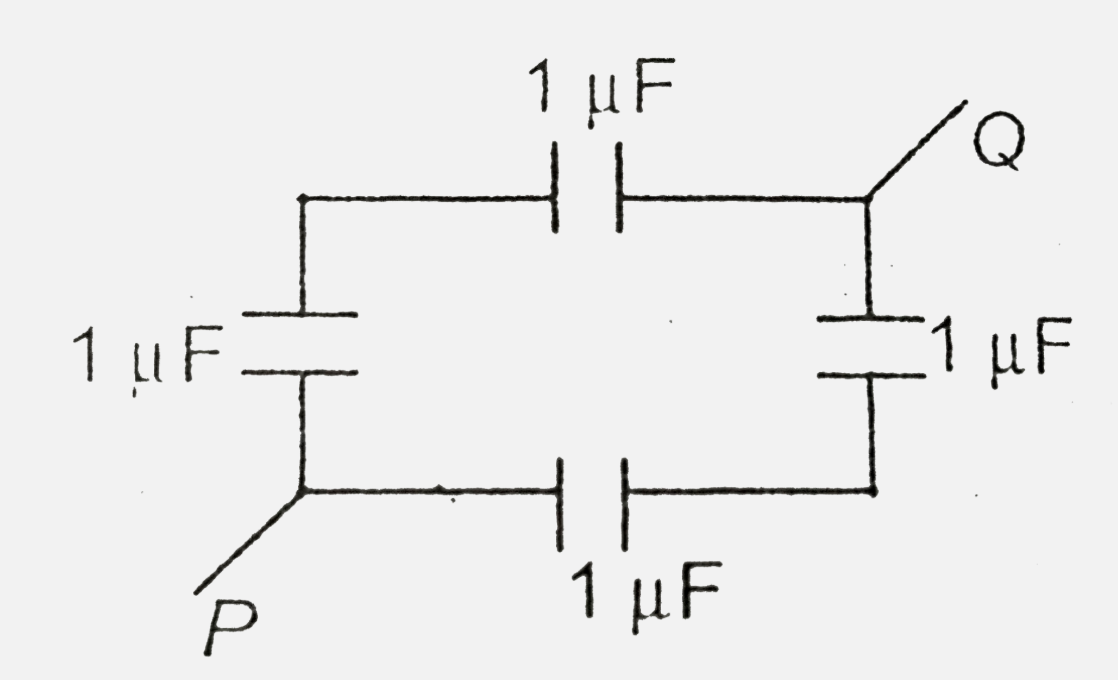
View SolutionFour capacitors are connected as shown in the figure. The equivalent capacitance between P and Q is

View Solution
