At the start of a motion along a line the initial velocity is u and acceleration is at. The final velocity vafter time t, is
v=u+at
v=u+at2
v=u+12at2
v=at2
The correct Answer is:B
To find the final velocity v after time t given the initial velocity u and acceleration a, we can follow these steps:
Step 1: Understand the relationship between acceleration, velocity, and time.
Acceleration a is defined as the rate of change of velocity with respect to time. Mathematically, this is expressed as:
a=dvdt
Step 2: Rearrange the equation for integration.
To find the change in velocity, we can rearrange the equation:
dv=adt
Step 3: Integrate both sides.
We will integrate both sides to find the relationship between velocity and time. The left-hand side will be integrated with respect to v and the right-hand side with respect to t:
∫dv=∫adt
Step 4: Set the limits of integration.
The limits for the left-hand side (velocity) will be from the initial velocity u to the final velocity v, and for the right-hand side (time), from 0 to t:
∫vudv=∫t0adt
Step 5: Solve the integrals.
The left-hand side gives:
v−u
The right-hand side, assuming a is constant, gives:
at
Step 6: Combine the results.
Now we can combine the results from both sides:
v−u=at
Step 7: Solve for final velocity v.
Rearranging the equation gives us:
v=u+at
Conclusion:
The final velocity v after time t is:
v=u+at
Acceleration a is defined as the rate of change of velocity with respect to time. Mathematically, this is expressed as:
a=dvdt
To find the change in velocity, we can rearrange the equation:
dv=adt
We will integrate both sides to find the relationship between velocity and time. The left-hand side will be integrated with respect to v and the right-hand side with respect to t:
∫dv=∫adt
The limits for the left-hand side (velocity) will be from the initial velocity u to the final velocity v, and for the right-hand side (time), from 0 to t:
∫vudv=∫t0adt
The left-hand side gives:
v−u
The right-hand side, assuming a is constant, gives:
at
Now we can combine the results from both sides:
v−u=at
Rearranging the equation gives us:
v=u+at
The final velocity v after time t is:
v=u+at
Similar Questions
If a particle starts moving with initial velocity u=1ms−1 and acceleration a=2ms−2, the veloctiy of the particle at any time is given by v=u+at=1+2t. Plot the velocity-time graph of the particle.
View SolutionIf a particle starts moving along x-axis from origin with initial velocity u=2m/s and acceleration 4m/s2 the relation between displacement and time is given as x=2t+2t2. Draw the displacement time graph for t>––––0.
View Solution
Knowledge Check
At the start of a motion along a line the initial velocity is u and acceleration is at. The final velocity v after time t, is
Av=u+atBv=u+at2Cv=u+12at2Dv=at2At the start of a motion along a line the initial velocity is u and acceleration is at. The final velocity v after timet, is
Av = u + atBv=u+at2Cv=u+12at2Dv=at2A particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
AconstantBabt2Cabt2mDa2bt2m
A particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
View SolutionA particle is moving along x-direction with a constant acceleration a. The particle starts from x=x0 position with initial velocity u. We can define the position of the particle with time by the relation
x=x0+ut+12at2
plot the position of the particle in relation with time is following situations
(i) If initial position of the particle is on negativ x-axis, initial velocity is positive and acceleration is negative.
(ii) If initial position is positive, initial velocity is negative and acceleration is positive.
View SolutionA particle is moving in a straight line with initial velocity u and uniform acceleration f. If the sum of the distances travelled in tthand(t+1)th seconds is 100cm, then its velocity after t seconds, in cm/s, is.
View SolutionFigure is a graph of the coordinate of a spider crawling along the x-axis. (a) Fraph tis velocity and acceleration as functionsof time. (b) In a motion diagram, show the position, velocity, and acceleration of the spider at the five times: t=2.5s, t=10 s, t=20 s, t=30 s,
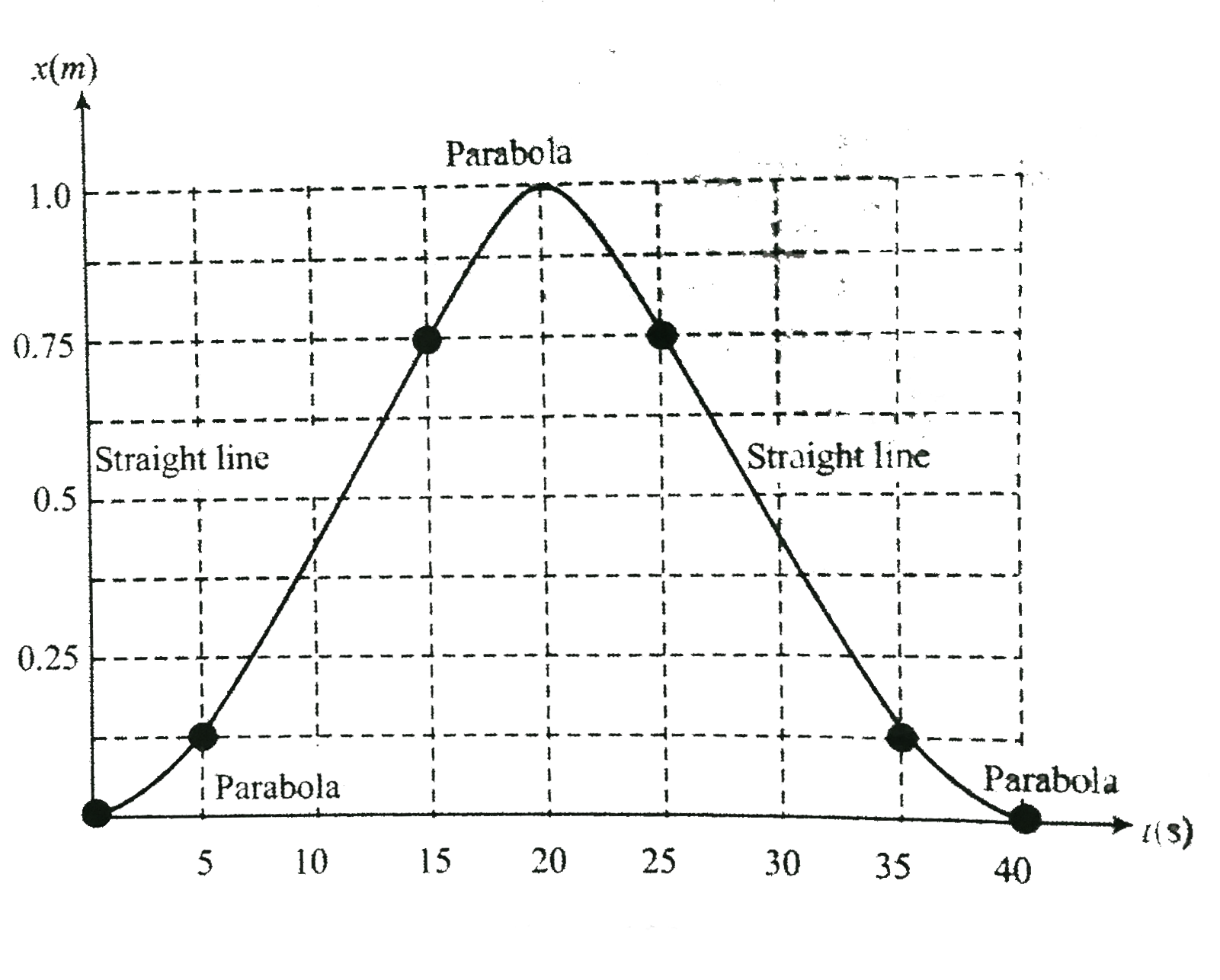 .
.
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at the origin .
View Solution
