A metal piece is heated up to T K. The temperature of the surrounding is t K. The heat lost to the surrounding due to radiation is proportional to
T4−t4
(T−t4)
(T4+t4)
(T4+t4)
The correct Answer is:A
To solve the problem of determining how the heat lost to the surrounding due to radiation is proportional, we can follow these steps:
Step 1: Understand the Concept of Radiation Heat Loss
The heat lost due to radiation from a surface is described by Stefan-Boltzmann Law, which states that the power radiated per unit area of a black body is proportional to the fourth power of its absolute temperature.
Step 2: Apply Stefan-Boltzmann Law
According to Stefan-Boltzmann Law, the heat loss Q due to radiation can be expressed as:
Q∝A(T4−t4)
where:
- A is the surface area of the metal piece,
- T is the absolute temperature of the metal piece,
- t is the absolute temperature of the surroundings.
Step 3: Identify the Proportionality
From the equation Q∝A(T4−t4), we can see that the heat loss is proportional to the difference in the fourth powers of the temperatures of the metal piece and its surroundings.
Step 4: Conclude the Proportionality
Thus, the heat lost to the surrounding due to radiation is proportional to:
(T4−t4)
Final Answer
The heat lost to the surrounding due to radiation is proportional to (T4−t4).
---
The heat lost due to radiation from a surface is described by Stefan-Boltzmann Law, which states that the power radiated per unit area of a black body is proportional to the fourth power of its absolute temperature.
According to Stefan-Boltzmann Law, the heat loss Q due to radiation can be expressed as:
Q∝A(T4−t4)
where:
- A is the surface area of the metal piece,
- T is the absolute temperature of the metal piece,
- t is the absolute temperature of the surroundings.
From the equation Q∝A(T4−t4), we can see that the heat loss is proportional to the difference in the fourth powers of the temperatures of the metal piece and its surroundings.
Thus, the heat lost to the surrounding due to radiation is proportional to:
(T4−t4)
The heat lost to the surrounding due to radiation is proportional to (T4−t4).
Similar Questions
A very thin metallic shell of radius r is heated to temperature T and then allowed to cool. The rate of cooling of shell is proportional to
View SolutionThree rods each of same length and cross - section are joined in series. The thermal conductivity of the materials are K, 2K and 3K respectively. If one end is kept at 200∘C and the other at 100∘C. What would be the temperature of the junctions in the steady state? Assume that no heat is lost due to radiation from the sides of the rods.
View Solution
Knowledge Check
- Question 1 - Select One
The resistance of an electrolyte varies with temperature T as RT=RO1+αT, where R0 and are constants. A constant potential difference V is applied to the two electrodes (each of surface area A) which are dipped in this electrolyte. If T0 is the temperature of the surroundings, the loss of heat to the surroundings per unit surface area put unit time is governed by the same relation H=k(T−T0)A, the steady state temperature is
A(V2+kAROT)(kROA−αV2)BV2kROA−αV2CV2RkADNone of these - Question 2 - Select One
A body at higher temperature T K radiates heat at a rate which is proportional to
ATBT2CT−4DT4 - Question 3 - Select One
A solid sphere and a hollow sphere of the same material and size are heated to the same temperature and allowed to cool in the same surroundings. If the temperature difference between the surroundings and each sphere is T, then :
AThe hollow sphere will cool at a faster rate for all values of TBThe solid sphere will cool at a faster rate for all values of TCBoth spheres will cool at the same rate for all values of TDBoth spheres will cool at the same rate only for small values of T
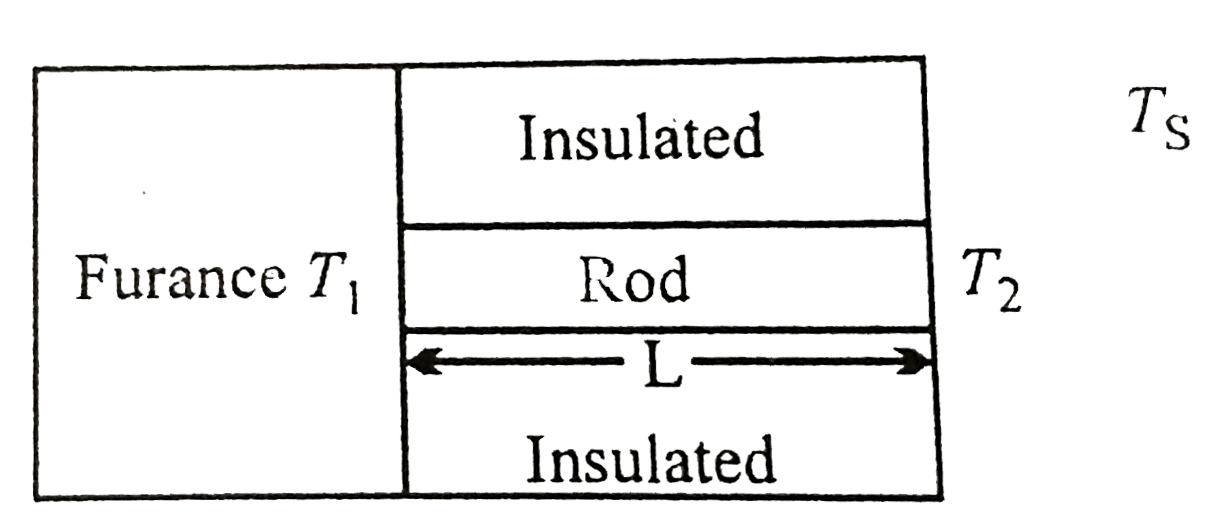
One end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
 View Solution
View SolutionA metal ball of mass 1.0 kg is kept in a room at 15∘C. It is heated using a heater. The heater supplies heat to the ball at a constant rate of 24 W. The temperature of the ball rises as shown in the graph. Assume that the rate of heat loss from the surface of the ball to the surrounding is proportional to the temperature difference between the ball and the surrounding. Calculate the rate of heat loss from the ball when it was at temperature of 20∘C.
 View Solution
View SolutionHeat energy will flow from our body to the surrounding if
View SolutionThe plane wall of an oven is of thickness L = 0.05 m and is exposed to the surrounding at 300 K. The outer surface of the oven exposed to the surrounding is at temperature 320 K in steady state. The energy radiated (In W/m2) by outer surface is proportional to the temperature difference between the surface and the surrounding, with proportionality constant 20W/m2K. What is the temperature of inner surface of the oven in steady state if the wall has a thermal conductivity of K = 0.5 W/mK
View SolutionIn an exothermic reaction heat is evolved and system loses heat to the surrounding. For such system
View Solution

