X-rays of wave length 1.54Å strike a crystal and are observed to be deflected at an angle 22.5∘ . Assuming that n = 1 , calculate the spacing between the planes of atom that are responsible for this reflection .
Applying Bragg equation ,
nλ=2dsinθ
Given n=1,λ=1.54Å,θ=22.5∘
d=1.542sin22.5∘=1.542×0.383
=2.01Å
Topper's Solved these Questions
- SOLID STATE BOOK - PREMIERS PUBLISHERSCHAPTER - SOLID STATE EXERCISE - OTHER IMPORTANT QUESTION &ANSWER ( CHOOSE THE CORRECT ANSWER )
26 Videos
- P-BLOCK ELEMENT IIBOOK - PREMIERS PUBLISHERSCHAPTER - P-BLOCK ELEMENT IIEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (ANSWER THE FOLLOWING QUESTIONS)
244 Videos
- SURFACE CHEMISTRYBOOK - PREMIERS PUBLISHERSCHAPTER - SURFACE CHEMISTRYEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (II. Answer the following questions:)
57 Videos
Similar Questions
X-rays of wavelength 1.54Ã… strike a crystal and are observed to be deflected at an angle of 22.5∘ . Assuming that n=1 , calculate the spacing between the planes of atoms that are responsible for this reflection.
View SolutionUsing X -rays of wavelength 154.1 pm and staring from the glancing angle, the reflection fro sliver crystal was found to occur at θ=22.20∘. Calculate the spacing between the planes of Ag atoms that gave rise to the above reflection. (sin22.20∘=0.3778)
View Solution
Knowledge Check
Wave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
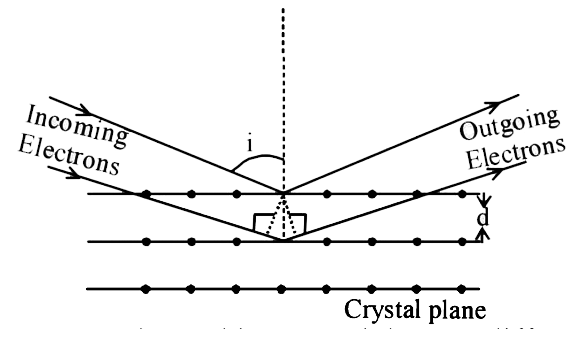
If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength λdB of electrons can be calculated by the relationship (n is an intenger)Adsini=nλdBB2dcosi=nλdBC2dsini=nλdBDdcosi=nλdB
Using X -rays of wavelength 154.1 pm and staring from the glancing angle, the reflection fro sliver crystal was found to occur at θ=22.20∘. Calculate the spacing between the planes of Ag atoms that gave rise to the above reflection. (sin22.20∘=0.3778)
View SolutionA parallel beam of X-rays with a wavelenght of 1.47 Å falls at a glancing angle of 31∘3' on a face of a rocksalt crystal. Find the spacing between the atomic planes of the crystal, if the second - order diffraction maximum is observed at this angle.
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely

If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength λdB of electrons can be calculated by the relationship (n is an intenger)
View SolutionA ray of light strikes a plane boundary separating two media, medium 1 and medium 2, at an angle of 45∘. Calculate the angle of refraction if the ray of light travels from medium 1 to medium 2. Given, refractive indices of medium 1 and 2 are 1.5 and 1.33 respectively.
View SolutionThe first order reflection of a beam of X-rays of wavelength 1.54 Ã… from the (100) face of a crystal of the simple cubic type occurs at an angle of 11.29∘ . Calculate the length of the unit cell.
View SolutionA right angle prism(45∘−90∘−45∘) of refractive index n has a plane of refractive index n1(n1<n) cemented to its diagonal face. The assembly is in air. The ray is incident on AB.
_E01_161_Q01.png)
(i) Calculate the angle of incidence at AB for which the ray strikes the diagonal face at the critical angle .
(ii) Assuming n = 1.352 , calculate the angle of incidence at AB for which the refracted ray passes through the diagonal face undeviated.
View SolutionA ball moving with a momentum of 5kgms−1 strikes against a wall at an angle of 45∘ and is reflected at the same angle. Calculate the change in momentum.
View Solution
