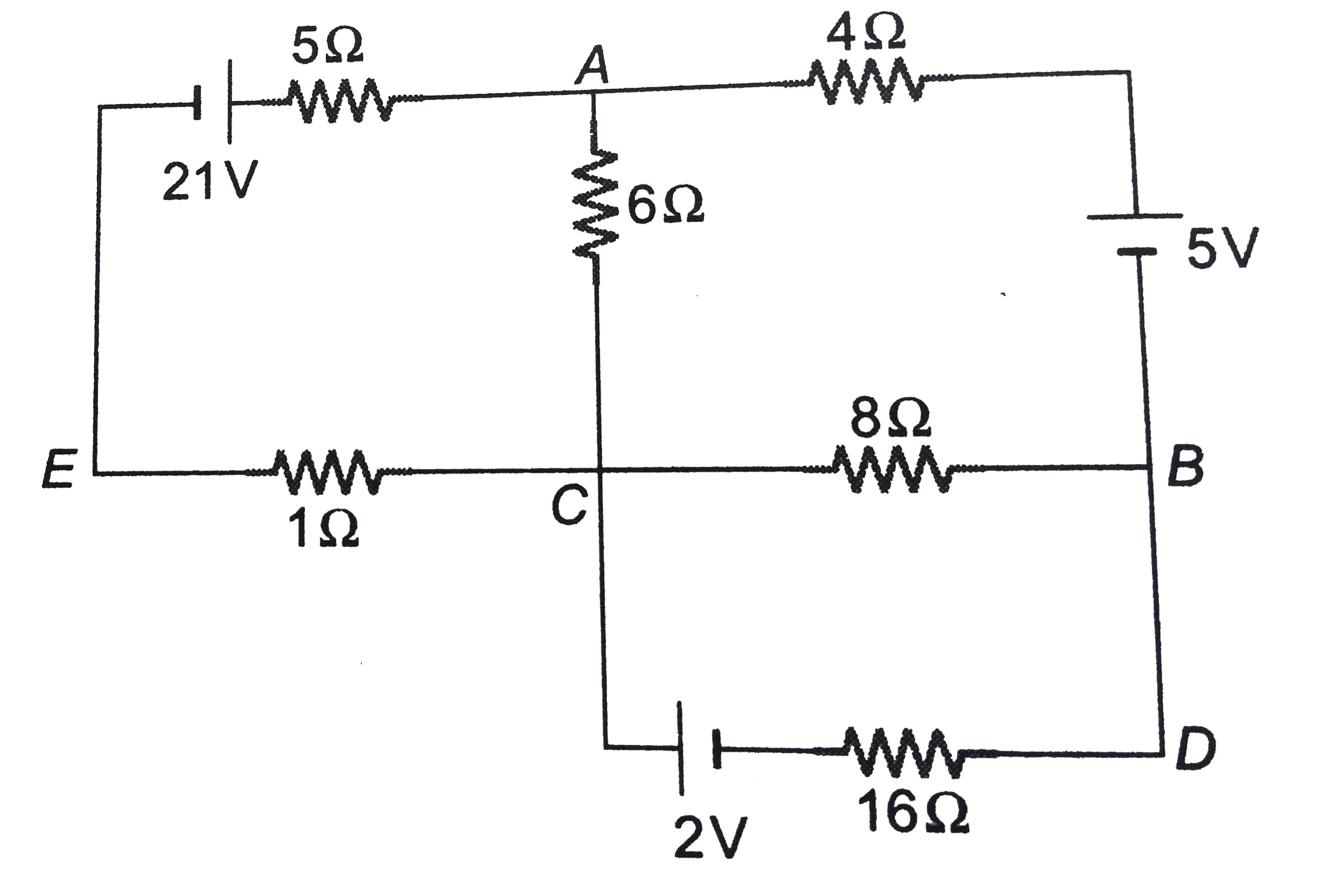
Reference to the problem 2 if R2 is short circuited and A and B are short circuited, find currents through each branch and the resistor R.
According to the question

Applying KVl at loop EFDCE,
2+l1−3=0⇒l1=1A
Applying KVL at loop EGHEF
1+l3−2=0⇒l3=1A
Applying KVL at loop HGABH ,
I4−l3−1=0⇒l4=2A
By kirchhoff.s first law,
l1+l2=l3+l4+⇒l2=2A
Similar Questions
Knowledge Check
- Question 1 - Select One
At the time of short circuit, the current in the circuit
Areduces substantiallyBdoes not changeCincreases heavilyDvaries continuously - Question 2 - Select One
At the time of short circuit, the current in the circuit
Areduces substantially.Bdoes not changeCincreases heavily.Dvary continuously. - Question 3 - Select One
At the time of short circuit, the current in the circuit
Areduces substantiallyBdoes not changeCincreases heavilyDvaries continuously
In the circuit in figure E1=3V,E2=2V,E3=1V and R=r1−r2−r3=1Ω
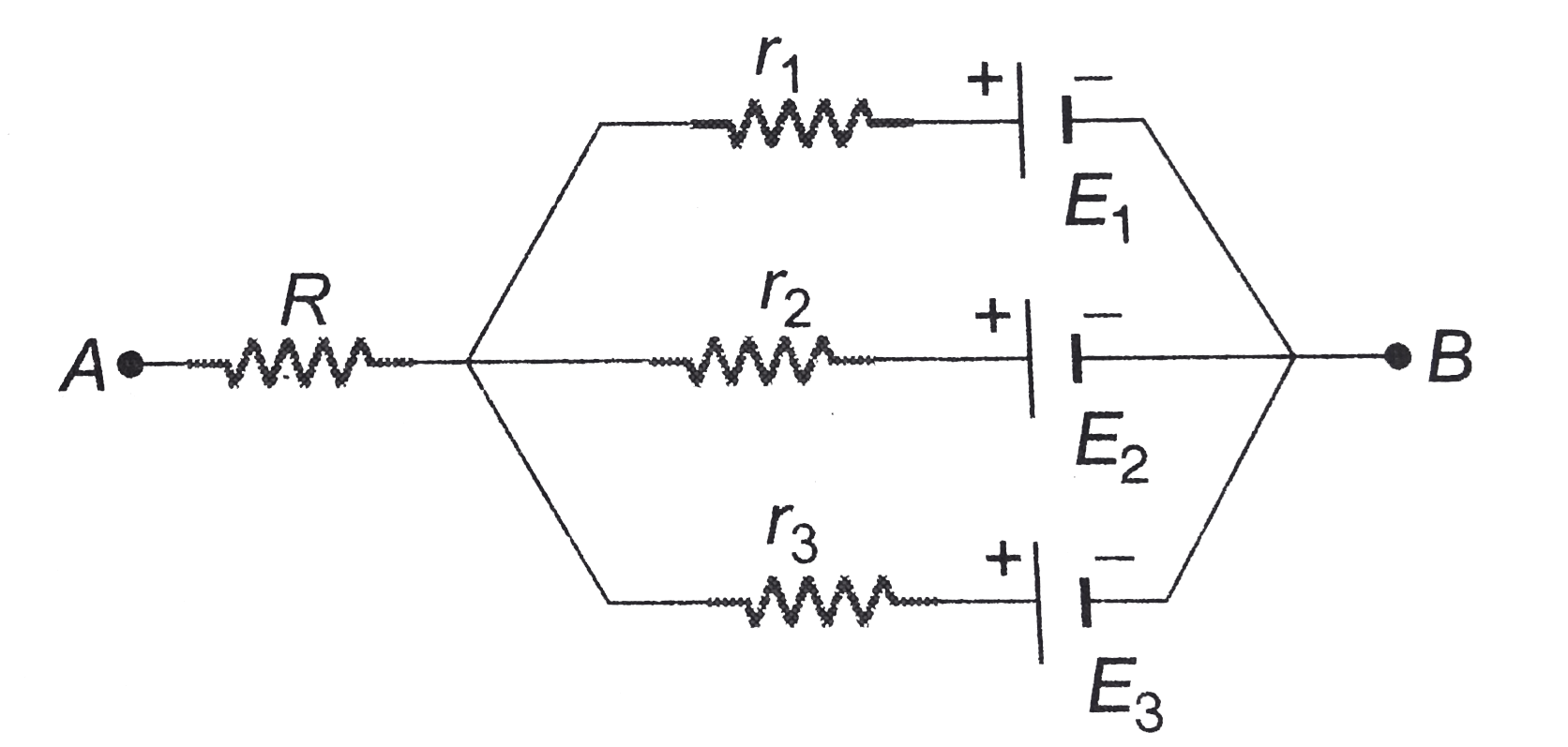
a. Find the potential differece between the points A and B and the currents through each branch.
b. If r2 is short circuited and the point A is connected to point B, find the currents through E1,E2,E3 and the resistor RView SolutionIn the circuit shown in fig E1=3vo<s,E2=2vo<s,E3=1vo<andR=r1=r2=r3=1ohm.
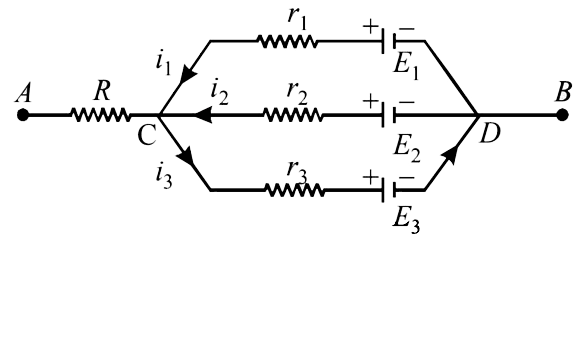
(i) Find the potential difference between the points A and B and the currents through each branch.
(ii) If r2 is short circuited and the point A is connected to point B, find the current through E1,E2,E3 and the resistor R.View SolutionDuring a short circuit, small amount of current flows through it.
View SolutionDuring a short circuit, small amount of current flows through it.
View SolutionIn the circuit shown , find the current through resistors.
 View Solution
View Solution