Question

Explain qualitatively single slit diffraction pattern showing the intensity distribution pattern .

Explanation

A parallel beam of light with a plane wavefront is made to fall on a single slit LN .As width of the slit LN = a is of the order of wavelength of light ,therefore diffraction occurs when beam of light passes througth the slit .
The wavelets from the single wavefront reach the centre C on the screen in same phase,Hence ,interfere constructively to give central maximum (bright fringe).
The diffraction pattern obtained on the screen consists of a central bright band ,having alternate dark and weak bright bands of decreasing intensity on both sedes.

Consider a point P on the screen at which wavelet travelling in a direction , make an angle `theta` with MC .The wavelets from points L and N will have a path difference equal to NQ . From the right angled `DeltaLNQ` , we have
`NQ=LNsintheta`
or `NQ=asintheta`
To establish the condition for secondary minima ,the slit is divided into 2,4,6,... equal parts such that correcponding wavelets from successive regions interfere with path difference of `lambda//2` .
Or for nth secondary minima ,the slit can be divided into 2n equal parts.
Hence ,for nth secondary minima ,
Path difference `=(a)/(2)"sin"theta=(lambda)/(2)`
or `sintheta_(n)=(nlambda)/(a),(n=1,2,3,...)`
To establish the condition for secondary maxima,the slit is divided into 3,5,7 ,... equal parts such that corresponding wavelets from alternate regions interfer with path difference of `lambda//2` .
Or for nth secondary maxima ,the slit can be divided into (2n+1) equal parts.
Hence ,for nth secondary maxima ,
`asintheta_(n)=(2n+1)(lambda)/(2) " " [n=1,2,3...]`
or `sintheta_(n)=(2n+1)(lambda)/(2a)`
Hence ,the diffraction pattern can be graphically shown as below

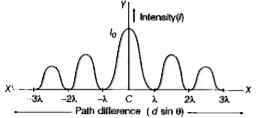
The point C corresponds to the position of central maxima .And the position `-3lambda,-2lambda,-lambda,lamda,2lambda,3lambda`.... are secondary minima . the above conditions for diffraction maxima and minima are exactly reverse of mathematical conditions for interference maxima and minima.