The side BC of a ΔABC is extended to D. If ∠ACD=120∘ and ∠ABC=12∠CAB, then the value of ∠ABC is
80∘
40∘
60∘
20∘
The correct Answer is:B
To solve the problem, we need to find the value of angle ABC given that angle ACD = 120° and angle ABC = (1/2) * angle CAB. Let's denote angle CAB as x and angle ABC as y.
1. Identify the angles:
- Let ∠ABC=y
- Let ∠CAB=x
- Given ∠ACD=120°
2. Use the relationship between angles:
- We know that ∠ABC=12∠CAB, which gives us:
y=12x
3. Apply the angle sum property in triangle ABC:
- In triangle ABC, the sum of the angles is 180°:
x+y+∠ACB=180°
- We also know that ∠ACB+∠ACD=180° because they are supplementary angles. Therefore:
∠ACB+120°=180°
- This implies:
∠ACB=180°−120°=60°
4. Substitute the known values into the triangle angle sum equation:
- Now substituting ∠ACB=60° into the angle sum equation:
x+y+60°=180°
5. Simplify the equation:
- Rearranging gives:
x+y=180°−60°=120°
6. Substitute y in terms of x:
- From step 2, we have y=12x. Substitute this into the equation:
x+12x=120°
7. Combine like terms:
- This simplifies to:
32x=120°
8. Solve for x:
- Multiply both sides by 23:
x=120°⋅23=80°
9. Find y:
- Now substitute x back to find y:
y=12x=12⋅80°=40°
Final Answer:
Thus, the value of ∠ABC is 40°.
- Let ∠ABC=y
- Let ∠CAB=x
- Given ∠ACD=120°
- We know that ∠ABC=12∠CAB, which gives us:
y=12x
- In triangle ABC, the sum of the angles is 180°:
x+y+∠ACB=180°
- We also know that ∠ACB+∠ACD=180° because they are supplementary angles. Therefore:
∠ACB+120°=180°
- This implies:
∠ACB=180°−120°=60°
- Now substituting ∠ACB=60° into the angle sum equation:
x+y+60°=180°
- Rearranging gives:
x+y=180°−60°=120°
- From step 2, we have y=12x. Substitute this into the equation:
x+12x=120°
- This simplifies to:
32x=120°
- Multiply both sides by 23:
x=120°⋅23=80°
- Now substitute x back to find y:
y=12x=12⋅80°=40°
Thus, the value of ∠ABC is 40°.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The side BC of Δ ABC is produced to D. If ∠ACD=108∘ and ∠B=12∠A then ∠A is
A36∘B72∘C108∘D59∘ - Question 2 - Select One
The side BC of ΔABC is produced to D. If ∠ACD=114∘ and ∠ABC=(12)∠BAC, what is the value (in degrees) of ∠BAC?
A36B48C76D84 - Question 3 - Select One
In the given figure, the value of ∠ABC is
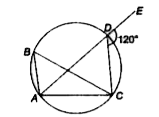 A70∘B45∘C60∘D30∘
A70∘B45∘C60∘D30∘
In a triangle ABC, the side BC is extended up to D. Such that CD = AC, if ∠BAD=109∘and∠ACB=72∘ then the value of ∠ABC is
View SolutionSide BC of △ABC produced to D if ∠ACD=108∘ and ∠B=12∠A then ∠A is
View SolutionIn a Δ ABC,BC is extended upto D:
∠ACD=120∘,∠B=12∠A. Then ∠A isView SolutionIn the triangle ABC,BC=CDand(∠ABC−∠BAC)=30∘. The measure of ∠ABD is :
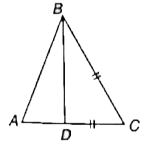 View Solution
View SolutionIn a ΔABC,∠BAC>90∘, then ∠ABC and ∠ACB must be :
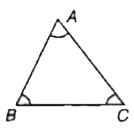 View Solution
View Solution

