The length of the chord of a circle is 8 cm and perpendicular distance between centre and the chord is 3 cm. Then the radius of the circle is equal to :
4 cm
5 cm
6 cm
8 cm
The correct Answer is:B
Step by step video, text & image solution for The length of the chord of a circle is 8 cm and perpendicular distance between centre and the chord is 3 cm. Then the radius of the circle is equal to : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length is
A√5 cmB2√5 cmC2√7 cmD√7 cm - Question 2 - Select One
In a circle, there are two chords opposite to the centre of the circle. The length of one chord and the radius of the circle is 6 cm and 5 cm respectively, and the distance between both the chords is 7 cm. Find the length of the second chord.
Aa) 8 cmBb) 10 cmCc) 6 cmDd) 14 cm - Question 3 - Select One
Two parallel chords are on one side of the centre of a circle. The length of the two chords is 24 cm and 32 cm. If the distance between the two chords is 8 cm, then what is the area (in cm2) of the circle?
A724.14B832.86C924.12D988.32
The radius of a circle is 10 cm and the perpendicular form the centre to a chord is 8cm. Find the length of the chord.
(ii) The radius of a circle is 10 cm. its one chord is 16 cm long. Find the perpendicular distance of this chord form the centre.
(iii) in the adjoining figure O is the centre of circle. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
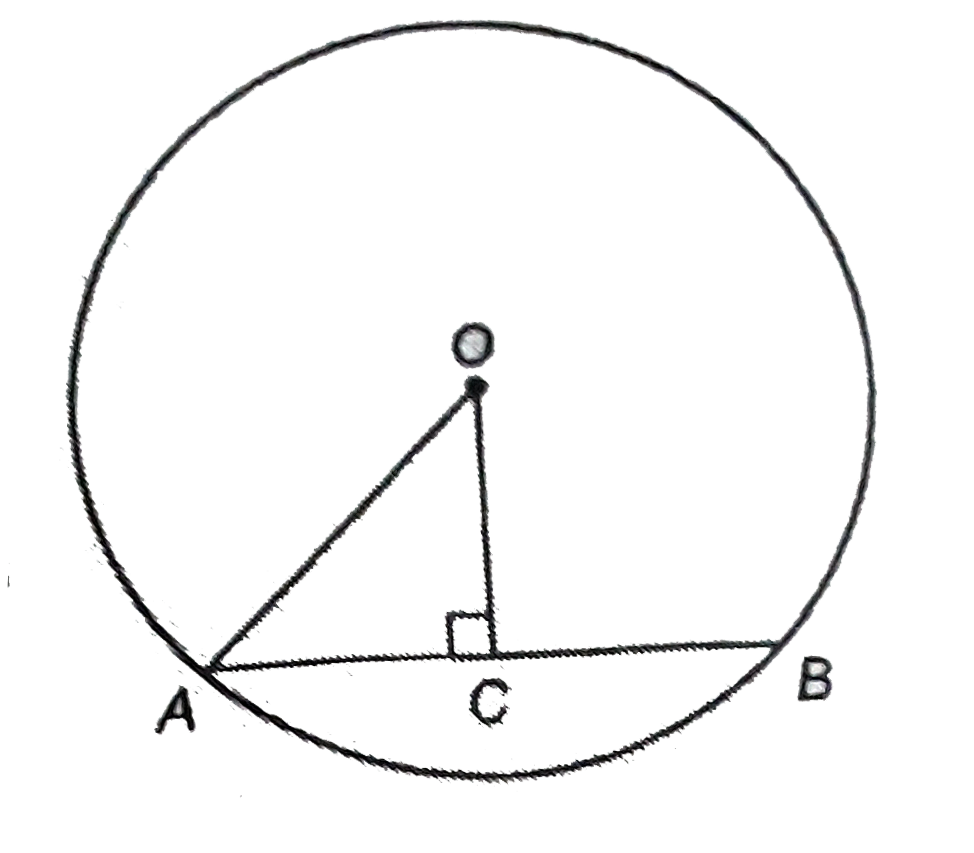
(iv) In the adjoining figure, OM⊥AB, radius OC=5cm and chord AB=8cm.Find the length of OM.
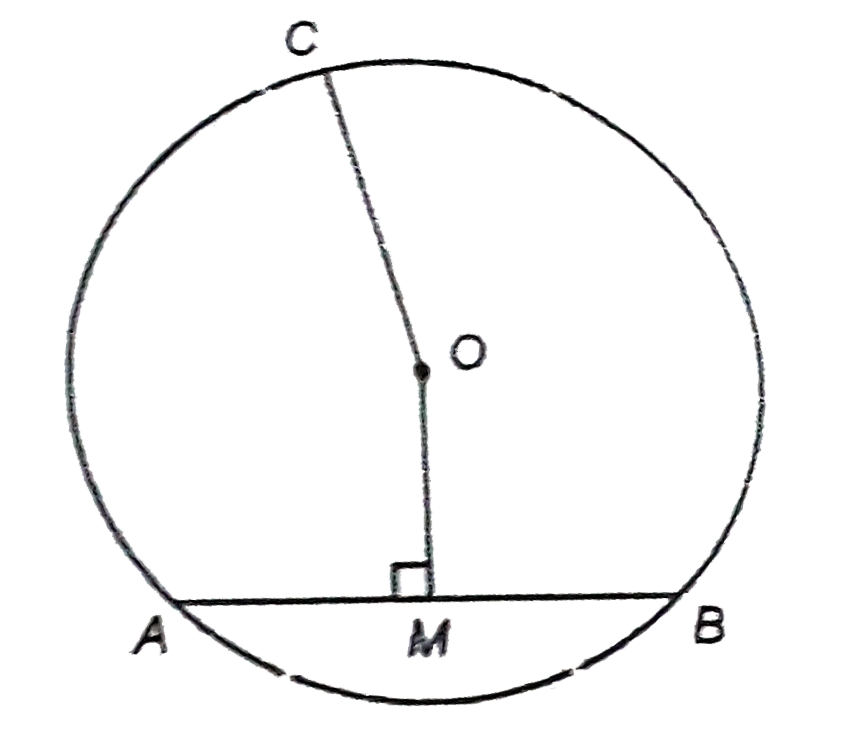 View Solution
View SolutionTwo parallel chords are on one side of the centre of a circle. The length of the two chords is 24 cm and 32 cm. If the distance between the two chords is 8 cm, then what is the area (in cm2) of the circle?
View SolutionThe length of a chord of a circle is equal to the radius of the circle. Compare the distance of the chord from the centre with the radius of the circle.
View SolutionCalculate the length (in cm) of the chord of the circle which is at the distance of the 12 cm from the centre and at the radius of the circle is 13 cm.
View SolutionThe length of a chord of a circle of radius 10 cm is 12 cm. Find the distance of the chord from the centre of the circle.
View Solution

