A square and a circle have equal perimeters. The ratio of the area of the square to the area of the circle is
1:1
1:4
π:2
π:4
The correct Answer is:D
To solve the problem where a square and a circle have equal perimeters and we need to find the ratio of the area of the square to the area of the circle, we can follow these steps:
1. Define the Perimeters:
- The perimeter of the square (P_square) is given by the formula:
Psquare=4×A
where A is the length of a side of the square.
- The perimeter of the circle (P_circle) is given by the formula:
Pcircle=2πr
where r is the radius of the circle.
2. Set the Perimeters Equal:
Since the perimeters are equal, we can set the two equations equal to each other:
4A=2πr
3. Solve for the Ratio Ar:
To find the ratio of the side of the square to the radius of the circle, we can rearrange the equation:
Ar=π2
4. Calculate the Areas:
- The area of the square (Area_square) is given by:
Areasquare=A2
- The area of the circle (Area_circle) is given by:
Areacircle=πr2
5. Find the Ratio of Areas:
We need to find the ratio of the area of the square to the area of the circle:
AreasquareAreacircle=A2πr2
6. Substitute Ar:
We can substitute Ar=π2 into the area ratio:
AreasquareAreacircle=A2πr2=(A/r)2⋅r2πr2=(π2)2⋅r2πr2
7. Simplify the Ratio:
The r2 terms cancel out:
AreasquareAreacircle=(π2)2π=π24π=π4
Final Answer:
The ratio of the area of the square to the area of the circle is:
π4
- The perimeter of the square (P_square) is given by the formula:
Psquare=4×A
where A is the length of a side of the square.
- The perimeter of the circle (P_circle) is given by the formula:
Pcircle=2πr
where r is the radius of the circle.
Since the perimeters are equal, we can set the two equations equal to each other:
4A=2πr
To find the ratio of the side of the square to the radius of the circle, we can rearrange the equation:
Ar=π2
- The area of the square (Area_square) is given by:
Areasquare=A2
- The area of the circle (Area_circle) is given by:
Areacircle=πr2
We need to find the ratio of the area of the square to the area of the circle:
AreasquareAreacircle=A2πr2
We can substitute Ar=π2 into the area ratio:
AreasquareAreacircle=A2πr2=(A/r)2⋅r2πr2=(π2)2⋅r2πr2
The r2 terms cancel out:
AreasquareAreacircle=(π2)2π=π24π=π4
The ratio of the area of the square to the area of the circle is:
π4
Topper's Solved these Questions
- BOOK - ARIHANT PUBLICATION PUNJABCHAPTER - MENSURATIONEXERCISE - Chapter Exercise83videos
MENSURATION
- BOOK - ARIHANT PUBLICATION PUNJABCHAPTER - MEASUREMENT SYSTEMEXERCISE - CHAPTER EXERCISE111videos
MEASUREMENT SYSTEM
- BOOK - ARIHANT PUBLICATION PUNJABCHAPTER - NUMBER SYSTEMEXERCISE - Example33videos
NUMBER SYSTEM
Similar Questions
The perimeters of a reqular hexagon and a square are equal. The ratio of the area of the square to the area of the hexagon is:
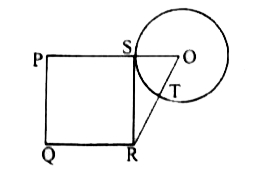
View SolutionPQRS is a square. SR is a tangent (at point S) to the circle with centre O and TR = OS. Then, the ratio of area of the square to the area of the circle is :
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The areas of a circle and a square are same. The ratio of the side of the square to the radius of the circle is
A2π:1B1:√πC√π:1D1:π - Question 2 - Select One
A circle and a square have same area. The ratio of the side of the square to the radius of the circle will be :
A(a) √π:1B(b) 1:√πC(c) π2:1D(d) 1:π - Question 3 - Select One
A circle and a square have same area. The ratio of the side of the square to the radius of the circle will be :
A√π:1B1:√πC1:πDπ:1
The diameter of a circle is equal to the side of the square. What is the area of the square if the area of the circle is 36 pi sq cm.
View SolutionAn equilateral triangle, a square and a circle have equal perimeters. If T denotes the area of triangle, S, the area of square and C, the area of the circle, then :
View SolutionA square and a regular hexagon have equal perimeters. Their areas are in the ratio:
View SolutionThe areas of a circle and a square are same. The ratio of the side of the square to the radius of the circle is
View SolutionThe area of square is 16π area of a circle. The ratio of the side of the square to the diameter of the circle is
View Solution

